本文主要是介绍笔记+R︱Logistics建模简述(logit值、sigmoid函数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本笔记源于CDA-DSC课程,由常国珍老师主讲。该训练营第一期为风控主题,培训内容十分紧凑,非常好,推荐:CDA数据科学家训练营
——————————————————————————————————
一、logit值的来源
逻辑回归一般将因变量二分类变量的0-1转变为频率[0,1],变成odds(优势比,[0,+∞]),然后log一下成为Logit值([-∞,+∞])

优势比就是:odds=P(y=1)/P(y=0)
logit值:logit=log(odds)
什么是sigmoid函数?
先定义了一个直觉的概念优势比 p/(1-p),p是true时的概率,1-p是false时的概率,对优势比取log,即t=log(p/(1-p))进行值域转换,转到所有实数域。然后反过来求p,最终即可得到sigmoid函数。

sigmoid函数的有趣特点是,自变量是负无穷到正无穷,应变量是0到1。越接近0变化越大。导函数是p(1-p),导函数很有趣。(参考:大话逻辑回归)
——————————————————————————————————
二、logit建模
利用logit=Y进行建模,得到Logit之后就可以根据其进行计算概率。Logit=经济学上的效用,效用是一个连续变量,logit模型相当于是效用建模。
所以一般来说,逻辑回归出来的系数都是logit值的系数,需要转化为概率值。简单的理解可以认为是:
输入是x,输出是y,中间有个临时变量是t。w和b是模型参数。h(t)是属于某个类别的概率,大于0.5认为属于这个类别,即y=1。
简便起见,我们可以认为b始终和一个值为1的w相乘。于是我们把b放入w。模型简化为
这就是逻辑回归的公式,非常简单。
(参考: 大话逻辑回归)——————————————————————————————————
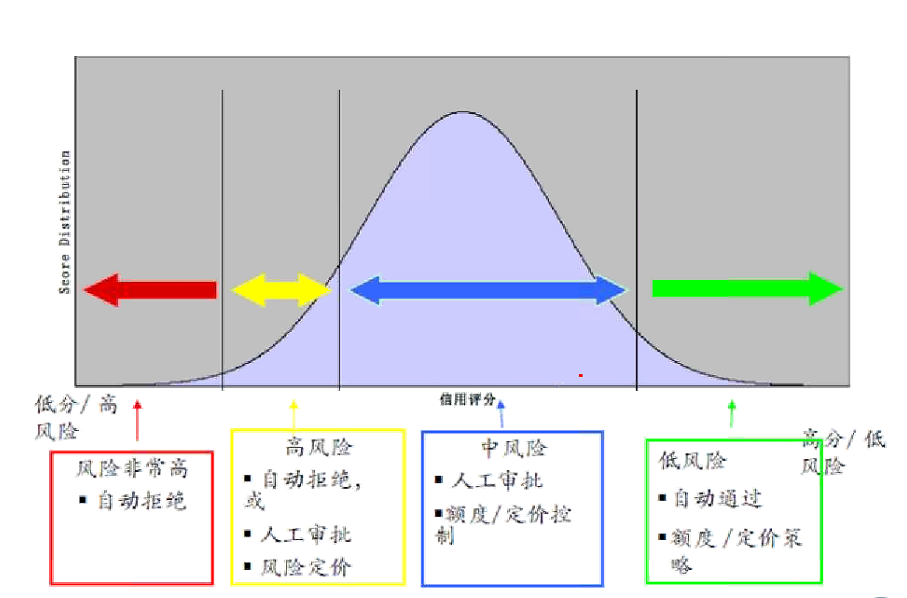
三、logit函数建模阀值设定
在风控模型汇总,logistics阀值的设置根据业务主来判断。一般高信用自动通过,中风险需要审查;风险较大的拒绝借贷。
——————————————————————————————————
四、R语言实现
1、逻辑回归
逻辑回归一般用glm函数中的binomial(link='logit')来建模。
lg<-glm(y ~x1,family=binomial(link='logit'))
summary(lg)此时的回归系数的用途只有两个:正负号、显著性.回归系数代表每增加1个单位x,会增加logit值增加0.1个单位,并且正向影响。如果需要知道概率值需要重新计算。
2、逐步回归筛选变量——step
在逻辑回归之上,我们可以用逐步回归方法,对变量进行剔除。
lg_ms<-step(lg,direction = "both")
summary(lg_ms)3、验证集预测——predict
train$lg_p<-predict(lg_ms, train)
summary(train$lg_p)predict的预测结果也同样是logit值,并不是概率,需要进行再计算
4、计算概率值
1/(1+exp(-1*train$lg_p))5、模型验证的方法
作为排序类模型,可以用ROC曲线/AUC值、累积提升曲线、K-S曲线、洛伦兹曲线gini来验证(笔记︱风控分类模型种类(决策、排序)比较与模型评估体系(ROC/gini/KS/lift))。
这篇关于笔记+R︱Logistics建模简述(logit值、sigmoid函数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









