本文主要是介绍[FNet]论文实现:FNet:Mixing Tokens with Fourier Transform,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1. 介绍
- 2. 架构
- 3. 结果
- 4. 总结
论文:FNet: Mixing Tokens with Fourier Transforms
作者:James Lee-Thorp, Joshua Ainslie, Ilya Eckstein, Santiago Ontanon
时间:2022
1. 介绍
transformer encode架构可以通过很多种方式进行加速,毫无例外的都是对attention mechanism 进行处理,通过把平方项的复杂度缩小到线性项的复杂度;
FNet没有用什么former后缀就表明,FNet并不是传统意义上transformer架构的优化,并不是在attention mechanism的优化;这里一个替换,利用线性的傅里叶变化替换掉注意力机制,在处理长文本的时候降低少许性能而巨大的提升训练推理速度和内存效率;
2. 架构
架构图如图所示,可以看到非常的清晰:
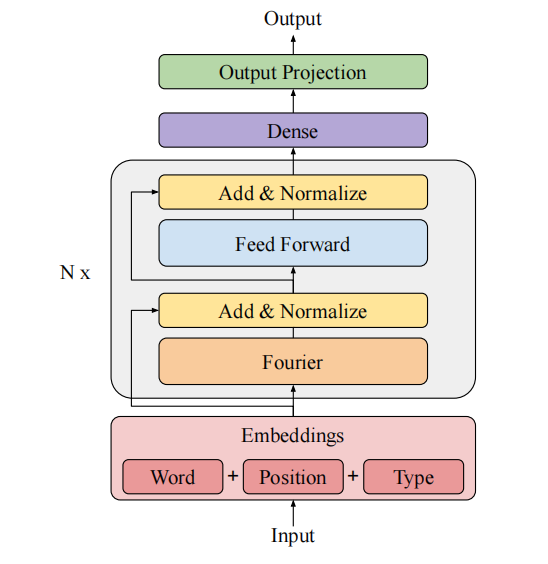
Discrete Fourier Transform(离散傅里叶变换): 对于 { x n } , n ∈ [ 0 , N − 1 ] \{x_n\},\quad n \in [0,N-1] {xn},n∈[0,N−1],有 { X k } \{X_k\} {Xk}如下:
X k = ∑ n = 0 N − 1 x n e − 2 π i N n k 0 ≤ k ≤ N − 1 X_k=\sum_{n=0}^{N-1}x_ne^{-\frac{2\pi i}{N}nk}\quad 0\leq k \leq N-1 Xk=n=0∑N−1xne−N2πink0≤k≤N−1
对于傅里叶变换的方式有两种方法,第一种就是简单的利用矩阵进行计算,有矩阵 W n k = ( e − 2 π i N n k / N ) , n , k = 1 , 2 , … , N − 1 W_{nk}=(e^{-\frac{2\pi i}{N}nk}/\sqrt N), \quad n,k=1,2,\dots,N-1 Wnk=(e−N2πink/N),n,k=1,2,…,N−1直接对序列乘个矩阵就好,另一种是FFT即the fast fourier transformer,采用最常见的算法是the Cooley–Tukey algorithm,将复杂度转化为 O ( N l o g N ) O(NlogN) O(NlogN);
这里利用离散傅里叶变换,对sequence求一次,对d_model求一次,得到最后的序列形状和原来的序列形状一样;最后得到的结果是一个复数,是无法使用的,我们要将其转化到实数域上来;但是这里要注意的是,是在两次fourier转化后,再进行实域转化;标准的fourier sublayer采用的是直接取实数部分的方式,论文还提到了三种其他的方式进行实域转化:Hadamard, Hartley 和 Discrete Cosine Transforms. 这里Hartley的效果和直接取实域的效果相当,其使用的方法是利用实部减去虚部的方式;
# 利用pytorch计算 2d fourier变换
x = nn.fft.fftn(x)
得到傅里叶变化序列后,经过一次残差连接和正态化,再经过一层前馈神经网络从d_model到隐藏维度,接着经过一次残差连接和正态化,再来一次前馈神经网络从隐藏维度到d_model;这就是一个fourier transformer block;
其他结构与transformer相同;
下面是模型的对比,可以看到FNet mat的mixing layer ops 操作数量是和Linaer的操作数量是一致的,因为原理都差不多,都是相当于左右各乘了一个矩阵;

但是利用FFT可以明显的看到优势;
为什么有这种效果:傅里叶转化有一个混合token的效果,而feed-forward sublayer有逆傅里叶转化的效果,傅里叶转化是把时域转化为频域,而feed-forward sublayer是一个矩阵,类似于inverse fourier transformer可以把频域转化为时域;
3. 结果
从下图中可以发现FNet-Hybrid的效果最接近于BERT
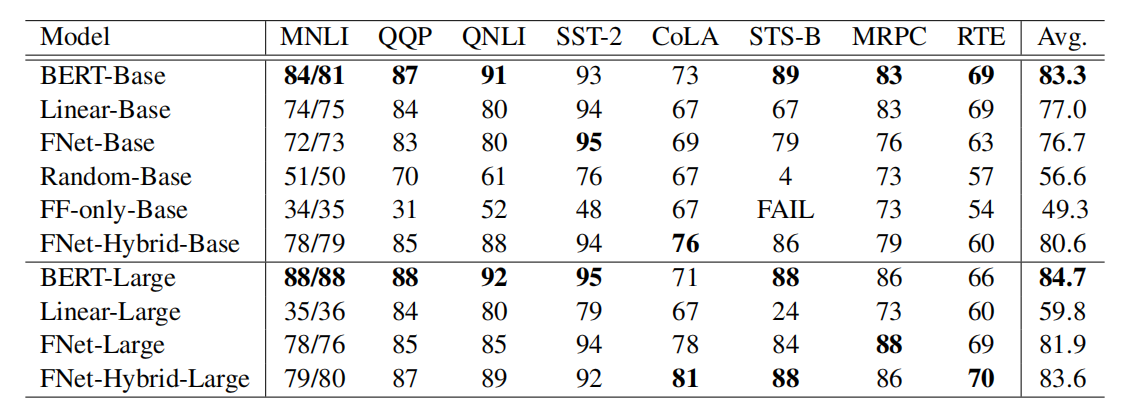
这里FNet-Hybrid意味着最后两层Fourier sublayer被替换成full attention sublayer;
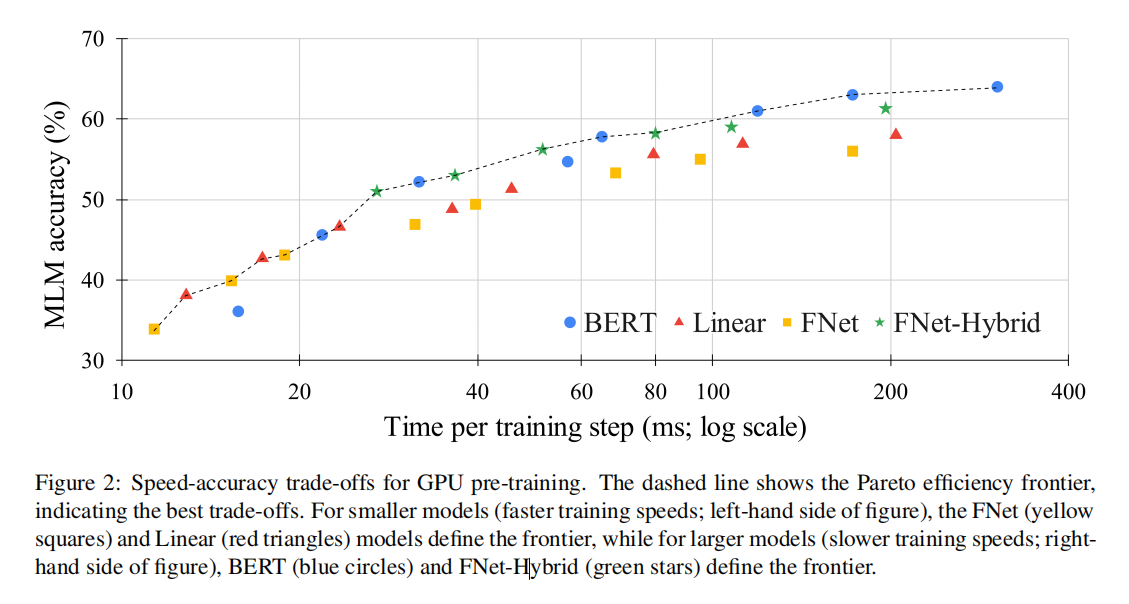
这图说明了对于更大、更慢的模型,BERT和FNet-Hybrid定义了the Pareto efficiency frontier;对于更小、更快的模型,FNet和线性模型定义了效率边界。
再看下图,感觉FNet的效果特别好;

4. 总结
TPU在计算矩阵相较于FFN有优势,而GPU在计算FFN相较于矩阵有优势;
FNet非常适合用于蒸馏,因为关键层没有权重;
FNet没有transformer decode,无法处理,未来需优化;
这篇关于[FNet]论文实现:FNet:Mixing Tokens with Fourier Transform的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





