蓝桥杯专题-真题版含答案-【骑士走棋盘】【阿姆斯壮数】【Shell 排序法 - 改良的插入排序】【合并排序法】

本文主要是介绍蓝桥杯专题-真题版含答案-【骑士走棋盘】【阿姆斯壮数】【Shell 排序法 - 改良的插入排序】【合并排序法】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Unity3D特效百例	案例项目实战源码	Android-Unity实战问题汇总
游戏脚本-辅助自动化	Android控件全解手册	再战Android系列
Scratch编程案例	软考全系列	Unity3D学习专栏
蓝桥系列	ChatGPT和AIGC

👉关于作者

专注于Android/Unity和各种游戏开发技巧，以及各种资源分享（网站、工具、素材、源码、游戏等）
有什么需要欢迎底部卡片私我，获取更多支持，交流让学习不再孤单。

👉实践过程

😜骑士走棋盘

说明骑士旅游（Knight tour）在十八世纪初倍受数学家与拼图迷的注意，它什么时候被提出已不可考，骑士的走法为西洋棋的走法，骑士可以由任一个位置出发，它要如何走完[所有的位置？
解法骑士的走法，基本上可以使用递回来解决，但是纯綷的递回在维度大时相当没有效率，一个聪明的解法由J.C. Warnsdorff在1823年提出，简单的说，先将最难的位置走完，接下来的路就宽广了，骑士所要走的下一步，「为下一步再选择时，所能走的步数最少的一步。」，使用这个方法，在不使用递回的情况下，可以有较高的机率找出走法（找不到走法的机会也是有的）。

#include <stdio.h> int board[8][8] = {0}; int main(void) {int startx, starty;int i, j;printf("输入起始点：");scanf("%d %d", &startx, &starty);if(travel(startx, starty)) {printf("游历完成！\n");}else {printf("游历失败！\n");}for(i = 0; i < 8; i++) {for(j = 0; j < 8; j++) {printf("%2d ", board[i][j]);}putchar('\n');}return 0;
} int travel(int x, int y) {// 对应骑士可走的八个方向int ktmove1[8] = {-2, -1, 1, 2, 2, 1, -1, -2};int ktmove2[8] = {1, 2, 2, 1, -1, -2, -2, -1};// 测试下一步的出路int nexti[8] = {0};int nextj[8] = {0};// 记录出路的个数int exists[8] = {0};int i, j, k, m, l;int tmpi, tmpj;int count, min, tmp;i = x;j = y;board[i][j] = 1;for(m = 2; m <= 64; m++) {for(l = 0; l < 8; l++) exists[l] = 0;l = 0;// 试探八个方向for(k = 0; k < 8; k++) {tmpi = i + ktmove1[k];tmpj = j + ktmove2[k];// 如果是边界了，不可走if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7)continue;// 如果这个方向可走，记录下来if(board[tmpi][tmpj] == 0) {nexti[l] = tmpi;nextj[l] = tmpj;// 可走的方向加一个l++;}}count = l;// 如果可走的方向为0个，返回if(count == 0) {return 0;}else if(count == 1) {// 只有一个可走的方向// 所以直接是最少出路的方向min = 0;}else {// 找出下一个位置的出路数for(l = 0; l < count; l++) {for(k = 0; k < 8; k++) {tmpi = nexti[l] + ktmove1[k];tmpj = nextj[l] + ktmove2[k];if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7) {continue;}if(board[tmpi][tmpj] == 0)exists[l]++;}}tmp = exists[0];min = 0;// 从可走的方向中寻找最少出路的方向for(l = 1; l < count; l++) {if(exists[l] < tmp) {tmp = exists[l];min = l;}}}// 走最少出路的方向i = nexti[min];j = nextj[min];board[i][j] = m;}return 1;
} 

😜阿姆斯壮数

说明
在三位的整数中，例如153可以满足13 + 53 + 33 = 153，这样的数称之为Armstrong数，试写出一程式找出所有的三位数Armstrong数。
解法
Armstrong数的寻找，其实就是在问如何将一个数字分解为个位数、十位数、百位数…，这只要使用除法与余数运算就可以了，例如输入 input为abc，则：
a = input / 100
b = (input%100) / 10
c = input % 10

#include <stdio.h> 
#include <time.h> 
#include <math.h> int main(void) { int a, b, c; int input; printf("寻找Armstrong数：\n"); for(input = 100; input <= 999; input++) { a = input / 100; b = (input % 100) / 10; c = input % 10; if(a*a*a + b*b*b + c*c*c == input) printf("%d ", input); } printf("\n"); return 0; 
}

😜Shell 排序法 - 改良的插入排序

说明
插入排序法由未排序的后半部前端取出一个值，插入已排序前半部的适当位置，概念简单但速度不快。

排序要加快的基本原则之一，是让后一次的排序进行时，尽量利用前一次排序后的结果，以加快排序的速度，Shell排序法即是基于此一概念来改良插入排序法。
解法
Shell排序法最初是D.L Shell于1959所提出，假设要排序的元素有n个，则每次进行插入排序时并不是所有的元素同时进行时，而是取一段间隔。

Shell首先将间隔设定为n/2，然后跳跃进行插入排序，再来将间隔n/4，跳跃进行排序动作，再来间隔设定为n/8、n/16，直到间隔为1之后的最 后一次排序终止，由于上一次的排序动作都会将固定间隔内的元素排序好，所以当间隔越来越小时，某些元素位于正确位置的机率越高，因此最后几次的排序动作将 可以大幅减低。

举个例子来说，假设有一未排序的数字如右：89 12 65 97 61 81 27 2 61 98

数字的总数共有10个，所以第一次我们将间隔设定为10 / 2 = 5，此时我们对间隔为5的数字进行排序，如下所示：

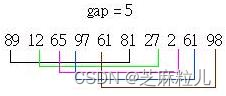
画线连结的部份表示 要一起进行排序的部份，再来将间隔设定为5 / 2的商，也就是2，则第二次的插入排序对象如下所示：

再来间隔设定为2 / 2 = 1，此时就是单纯的插入排序了，由于大部份的元素都已大致排序过了，所以最后一次的插入排序几乎没作什么排序动作了：

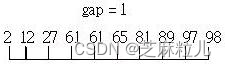
将间隔设定为n / 2是D.L Shell最初所提出，在教科书中使用这个间隔比较好说明，然而Shell排序法的关键在于间隔的选定，例如Sedgewick证明选用以下的间隔可以加 快Shell排序法的速度：

其中4*(2j)2 + 3*(2j) + 1不可超过元素总数n值，使用上式找出j后代入4*(2j)2 + 3*(2j) + 1求得第一个间隔，然后将2j除以2代入求得第二个间隔，再来依此类推。

后来还有人证明有其它的间隔选定法可以将Shell排序法的速度再加快；另外Shell排序法的概念也可以用来改良气泡排序法。

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void shellsort(int[]); int main(void) { int number[MAX] = {0}; int i;  srand(time(NULL)); printf("排序前："); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; printf("%d ", number[i]); } shellsort(number); return 0; 
} void shellsort(int number[]) { int i, j, k, gap, t; gap = MAX / 2; while(gap > 0) { for(k = 0; k < gap; k++) { for(i = k+gap; i < MAX; i+=gap) { for(j = i - gap; j >= k; j-=gap) { if(number[j] > number[j+gap]) { SWAP(number[j], number[j+gap]); } else break; } } } printf("\ngap = %d：", gap); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n"); gap /= 2; } 
}

😜合并排序法

说明之前所介绍的排序法都是在同一个阵列中的排序，考虑今日有两笔或两笔以上的资料，它可能是不同阵列中的资料，或是不同档案中的资料，如何为它们进行排序？
解法可以使用合并排序法，合并排序法基本是将两笔已排序的资料合并并进行排序，如果所读入的资料尚未排序，可以先利用其它的排序方式来处理这两笔资料，然后再将排序好的这两笔资料合并。

有人问道，如果两笔资料本身就无排序顺序，何不将所有的资料读入，再一次进行排序？排序的精神是尽量利用资料已排序的部份，来加快排序的效率，小笔资料的 排序较为快速，如果小笔资料排序完成之后，再合并处理时，因为两笔资料都有排序了，所有在合并排序时会比单纯读入所有的资料再一次排序来的有效率。

那么可不可以直接使用合并排序法本身来处理整个排序的动作？而不动用到其它的排序方式？答案是肯定的，只要将所有的数字不断的分为两个等分，直到最后剩一个数字为止，然后再反过来不断的合并，就如下图所示：

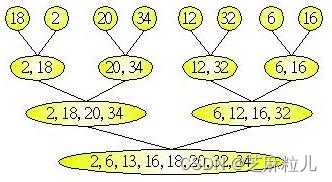
不过基本上分割又会花去额外的时间，不如使用其它较好的排序法来排序小笔资料，再使用合并排序来的有效率。
下面这个程式范例，我们使用快速排序法来处理小笔资料排序，然后再使用合并排序法处理合并的动作。

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX1 10 
#define MAX2 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} int partition(int[], int, int); 
void quicksort(int[], int, int); 
void mergesort(int[], int, int[], int, int[]); int main(void) { int number1[MAX1] = {0}; int number2[MAX1] = {0}; int number3[MAX1+MAX2] = {0}; int i, num;  srand(time(NULL)); printf("排序前："); printf("\nnumber1[]："); for(i = 0; i < MAX1; i++) { number1[i] = rand() % 100; printf("%d ", number1[i]); } printf("\nnumber2[]："); for(i = 0; i < MAX2; i++) { number2[i] = rand() % 100; printf("%d ", number2[i]); } // 先排序两笔资料 quicksort(number1, 0, MAX1-1); quicksort(number2, 0, MAX2-1); printf("\n排序后："); printf("\nnumber1[]："); for(i = 0; i < MAX1; i++) printf("%d ", number1[i]); printf("\nnumber2[]："); for(i = 0; i < MAX2; i++) printf("%d ", number2[i]); // 合并排序 mergesort(number1, MAX1, number2, MAX2, number3); printf("\n合并后："); for(i = 0; i < MAX1+MAX2; i++) printf("%d ", number3[i]); printf("\n"); return 0; 
} int partition(int number[], int left, int right) { int i, j, s; s = number[right]; i = left - 1; for(j = left; j < right; j++) { if(number[j] <= s) { i++; SWAP(number[i], number[j]); } } SWAP(number[i+1], number[right]); return i+1; 
} void quicksort(int number[], int left, int right) { int q; if(left < right) { q = partition(number, left, right); quicksort(number, left, q-1); quicksort(number, q+1, right); } 
} void mergesort(int number1[], int M, int number2[], int N, int number3[]) { int i = 0, j = 0, k = 0; while(i < M && j < N) { if(number1[i] <= number2[j]) number3[k++] = number1[i++]; else number3[k++] = number2[j++]; } while(i < M) number3[k++] = number1[i++]; while(j < N) number3[k++] = number2[j++]; 
} 

👉其他

📢作者：小空和小芝中的小空
📢转载说明-务必注明来源：https://zhima.blog.csdn.net/
📢这位道友请留步☁️，我观你气度不凡，谈吐间隐隐有王者霸气💚，日后定有一番大作为📝！！！旁边有点赞👍收藏🌟今日传你，点了吧，未来你成功☀️，我分文不取，若不成功⚡️，也好回来找我。

温馨提示：点击下方卡片获取更多意想不到的资源。

这篇关于蓝桥杯专题-真题版含答案-【骑士走棋盘】【阿姆斯壮数】【Shell 排序法 - 改良的插入排序】【合并排序法】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---