本文主要是介绍pl_vio线特征·part I,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
pl_vio线特征
- 0.引言
- 1.LineFeatureTracker核心逻辑解读
- 2.estimator_node中线段的处理
- 2.1.订阅信息解压
- 2.2.线特征管理
- 3.线段的表示与三角化
- 3.1.普吕克线坐标
- 3.2.正交表示
- 4.线段残差对位姿的导数
- 4.1.直线的观测模型和误差
- 4.2.误差雅克比推导
0.引言
-
pl_vio线特征·part II
-
PL-VIO,本文关注线段。
-
论文链接
-
SLAM中线特征的参数化和求导
-
SLAM线特征学习(1)——基本的线特征表示与优化推导
-
SLAM线特征学习(2)——线特征初始化和最小表示
-
SLAM中线特征的参数化表示方法/重投影/初始化方法
1.LineFeatureTracker核心逻辑解读
-
数据结构定义:
-
keylsd:提取的线段结果(经过长度筛选的,太短的不要)
-
keylbd_descr:对应线段描述子结果(经过长度筛选的,太短的不要)
-
新进的img提取线特征:
- 如果是第一帧img:forwframe_->lineID.push_back(allfeature_cnt++);(allfeature_cnt是整个系统全局的线特征计数),因此lineID是全局的ID,整个系统中线特征具有唯一的ID。update:后面更新的是没匹配上的。
- 如果不是第一帧img,则暂时赋值为-1,但forwframe_->lineID数组的size的大小是和keylsd相同的;
- 匹配后将-1进行更改:forwframe_->lineID[mt.queryIdx] = curframe_->lineID[mt.trainIdx];
- Key = 当前帧线段的ID
- Value = 前一帧线段的lineID[mt.trainIdx]
- 判断当前帧水平,垂直方向线段数量是否分别足够35条,不够的补上。
- 匹配后将-1进行更改:forwframe_->lineID[mt.queryIdx] = curframe_->lineID[mt.trainIdx];
匹配的结果,对应关系,其实就是存储的全局ID信息。
代码注释,可惜另一个函数的关键内容lineDetector没放出来,这个函数的vecLine只在最后做了一个转换。frame_id没维护。
字数超限,删除代码,代码是这个函数。
最后forwframe_->vecLine属性,赋值了三个
l.StartPt = lsd.getStartPoint();
l.EndPt = lsd.getEndPoint();
l.length = lsd.lineLength;
ROS发布的信息
- feature_lines->points : 线段起点
- feature_lines->channels.push_back(id_of_line); :与上一帧的匹配关系
- feature_lines->channels.push_back(u_of_endpoint);:线段终点 u 坐标
- feature_lines->channels.push_back(v_of_endpoint);:线段终点 v 坐标
在ROS中,sensor_msgs::PointCloud是一个用于表示3D点云的消息类型。它的数据结构如下:
- std_msgs/Header header:消息头,包含时间戳和坐标帧信息。
- geometry_msgs/Point32[] points:点云中的点,每个点包含x、y和z坐标。
- std_msgs/ChannelFloat32[] channels:每个通道包含一个名字和一组与点对应的浮点数。这可以用来存储与每个点相关的额外数据,如颜色、强度等,这里存储的信息如上所述。
2.estimator_node中线段的处理
2.1.订阅信息解压
map<int, vector<pair<int, Vector4d>>> lines;
for (unsigned int i = 0; i < line_msg->points.size(); i++) {int v = line_msg->channels[0].values[i] + 0.5;// std::cout<< "receive id: " << v / NUM_OF_CAM << "\n";int feature_id = v / NUM_OF_CAM;int camera_id =v % NUM_OF_CAM; // 被几号相机观测到的,如果是单目,camera_id = 0double x_startpoint = line_msg->points[i].x;double y_startpoint = line_msg->points[i].y;double x_endpoint = line_msg->channels[1].values[i];double y_endpoint = line_msg->channels[2].values[i];// ROS_ASSERT(z == 1);lines[feature_id].emplace_back(camera_id,Vector4d(x_startpoint, y_startpoint, x_endpoint, y_endpoint));
}
map<int, vector<pair<int, Vector4d>>> lines; 其实这里的vetor大小始终是1
- key : 与上一帧线特征的对应关系
- value : camera_id + 线段起点 + 线段终点
2.2.线特征管理
现根据之前匹配的对应关系构造出lineFeaturePerId信息:
// 根据frame进行维护,这里是最初读取的数据
class lineFeaturePerFrame {public:lineFeaturePerFrame(const Vector4d &line) { lineobs = line; }lineFeaturePerFrame(const Vector8d &line) {lineobs = line.head<4>();lineobs_R = line.tail<4>();}Vector4d lineobs; // 每一帧上的观测Vector4d lineobs_R;double z;bool is_used;double parallax;MatrixXd A;VectorXd b;double dep_gradient;
};// 根据id进行维护,该id的线段可能被多帧观测到
class lineFeaturePerId {public:const int feature_id; //线特征的全局ID,全局唯一int start_frame;// linefeature_per_frame 是个向量容器,存着这个特征在每一帧上的观测量。// 如:feature_per_frame[0],存的是ft在start_frame上的观测值;// feature_per_frame[1]存的是start_frame+1上的观测// 同一id在不同帧上的观测,统一放到一起,后续会进行三角化vector<lineFeaturePerFrame> linefeature_per_frame;int used_num;bool is_outlier;bool is_margin;bool is_triangulation;Vector6d line_plucker;Vector4d obs_init;Vector4d obs_j;Vector6d line_plk_init; // used to debugVector3d ptw1; // used to debugVector3d ptw2; // used to debugEigen::Vector3d tj_; // tijEigen::Matrix3d Rj_;Eigen::Vector3d ti_; // tijEigen::Matrix3d Ri_;int removed_cnt;int all_obs_cnt; // 这个id的线特征总共被观测了多少次int solve_flag; // 0 haven't solve yet; 1 solve succ; 2 solve fail;int endFrame();
};
构造的逻辑,理解了之前的对应关系是怎么存储的这里就很好理解了:
// 遍历同一帧上的线特征for (auto &id_line : lines) {// 使用起点终点初始化lineFeaturePerFrame f_per_fra(id_line.second[0].second); // 观测// 这是与上一帧的匹配关系,也可以认为是全局线特征idint feature_id = id_line.first; // cout << "line id: "<< feature_id << "\n";// 在feature里找id号为feature_id的特征auto it = find_if(linefeature.begin(), linefeature.end(),[feature_id](const lineFeaturePerId &it) {return it.feature_id == feature_id;});// 如果之前没存这个特征,说明是新的if (it == linefeature.end()) {linefeature.push_back(lineFeaturePerId(feature_id, frame_count));linefeature.back().linefeature_per_frame.push_back(f_per_fra);} else if (it->feature_id == feature_id) {it->linefeature_per_frame.push_back(f_per_fra);it->all_obs_cnt++;}}
3.线段的表示与三角化
- 这部分来自论文原文。
- 初始化和进行空间变换的时候使用Plücker坐标,
- 在优化的时候使用正交表示。
- 坐标表示
- 普吕克坐标: L = ( n ⊤ , v ⊤ ) ⊤ ∈ R 6 \mathcal{L}=\left(\mathbf{n}^{\top}, \mathbf{v}^{\top}\right)^{\top} \in \mathbb{R}^6 L=(n⊤,v⊤)⊤∈R6
- 正交表示: ( U , W ) ∈ S O ( 3 ) × S O ( 2 ) (\mathbf{U},\mathbf{W}) \in SO(3) \times SO(2) (U,W)∈SO(3)×SO(2)
3.1.普吕克线坐标
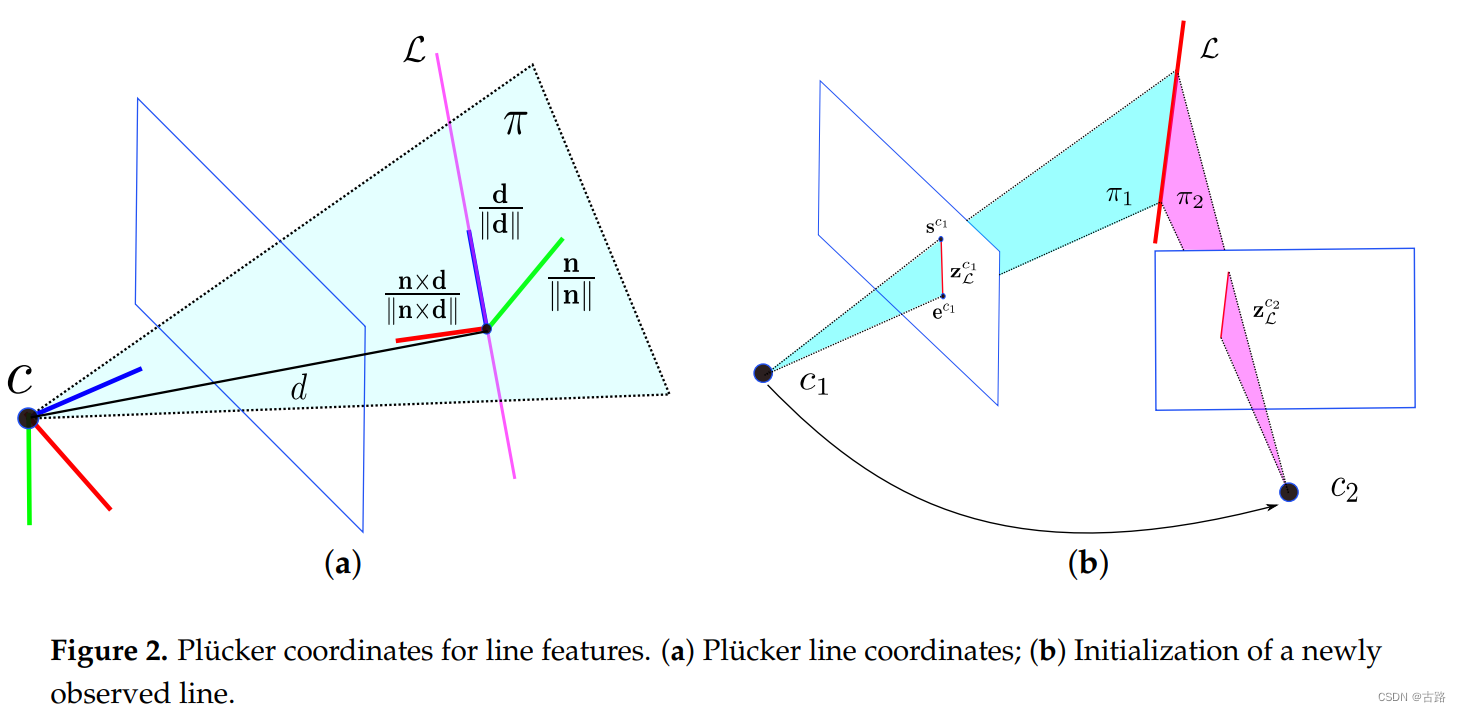
在图 2 a 2 \mathrm{a} 2a 中, 普吕克坐标中的 3 D 3 \mathrm{D} 3D 空间线 L \mathcal{L} L 由 L = ( n ⊤ , d ⊤ ) ⊤ ∈ R 6 \mathcal{L}=\left(\mathbf{n}^{\top}, \mathrm{d}^{\top}\right)^{\top} \in \mathbb{R}^6 L=(n⊤,d⊤)⊤∈R6 表示, 其中 d ∈ R 3 \mathrm{d} \in \mathbb{R}^3 d∈R3 是线方向向量, n ∈ R 3 \mathrm{n} \in \mathbb{R}^3 n∈R3 是由直线和坐标原点确定的平面法向量。Plücker 坐标被过度参数化,因为向量 n \mathrm{n} n 和 d \mathrm{d} d 之间存在隐式约束,即 n ⊤ d = 0 \mathrm{n}^{\top} \mathrm{d}=0 n⊤d=0 。因此, Plücker坐标不能直接用于无约束优化。然而, 使用由法线向量和方向向量表示的 3D 线, 可以简单地从两个几何视图执行三角测量, 并且也可以方便地对线几何变换进行建模。
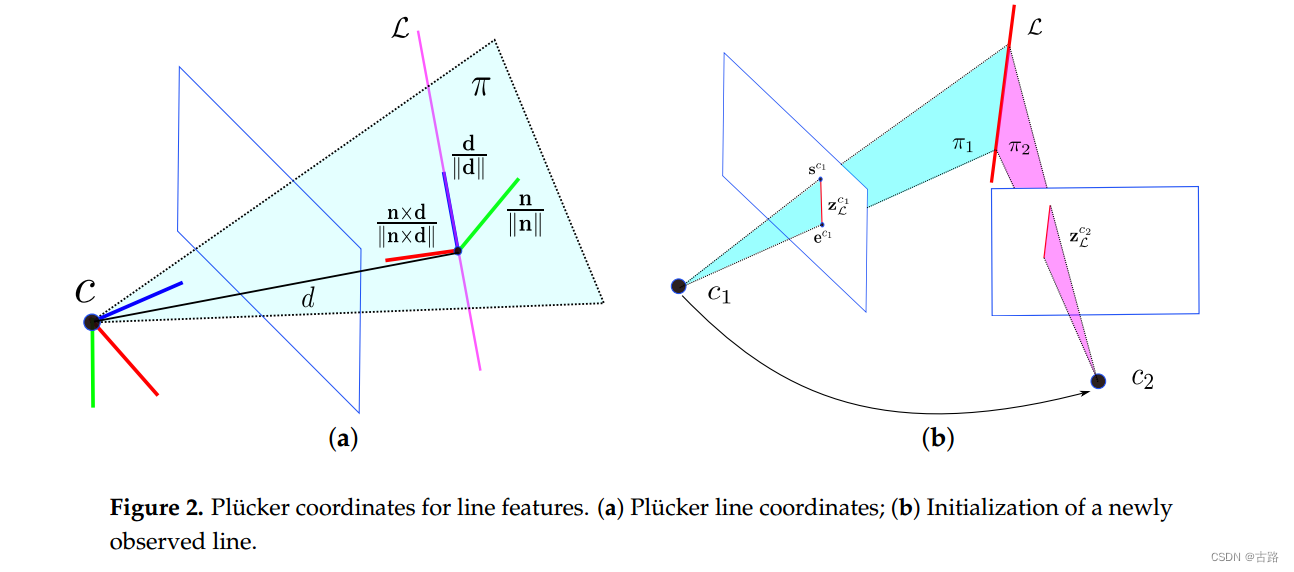

对于线几何变换, 给定从世界坐标系 w \mathrm{w} w 到相机坐标系 c \mathrm{c} c 的变换矩阵 T c w = [ R c w P c w 0 1 ] \mathbf{T}_{c w}=\left[\begin{array}{cc}\mathbf{R}_{c w} & \mathbf{P}_{c w} \\ \mathbf{0} & \mathbf{1}\end{array}\right] Tcw=[Rcw0Pcw1], 我们可以将线的 Plücker 坐标变换为 [30]
L c = [ n c d c ] = J c w L w = [ R c w [ p c w ] x R c w 0 R c w ] L w \mathcal{L}^c=\left[\begin{array}{c} \mathbf{n}^c \\ \mathbf{d}^c \end{array}\right]=J_{c w} \mathcal{L}_w=\left[\begin{array}{cc} \mathbf{R}_{c w} & {\left[\mathbf{p}_{c w}\right]_x \mathbf{R}_{c w}} \\ 0 & \mathbf{R}_{c w} \end{array}\right] \mathcal{L}^w Lc=[ncdc]=JcwLw=[Rcw0[pcw]xRcwRcw]Lw
其中 [ ⋅ ] × [\cdot]_{\times} [⋅]×是三维向量的斜对称矩阵, J c w J_{c w} Jcw 是用于将线从帧 w w w 变换到帧 c \mathrm{c} c 的变换矩阵。
当在两个不同的摄像机视图中观察到新的线地标时,可以轻松计算出普吕克坐标。如图 2 b 2 \mathrm{~b} 2 b 所示,3D 线 L \mathcal{L} L 由摄像机 c 1 c_1 c1 和 c 2 c_2 c2 捕获为 z L c 1 \mathrm{z}_L^{c_1} zLc1 和 z l c 2 \mathrm{z}_l^{c_2} zlc2。归一化图像平面中的线段 z L c 1 \mathrm{z}_L^{c_1} zLc1 可以由两个端点 s c 1 = [ u s , v s , 1 ] T \mathrm{s}^{c_1}=\left[u_s, v_s, 1\right]^T sc1=[us,vs,1]T 和 e c 1 = [ u e , v e , 1 ] ⊤ \mathrm{e}^{c_1}=\left[u_e, v_e, 1\right]^{\top} ec1=[ue,ve,1]⊤ 表示。三个不共线的点,包括线段的两个端点和坐标原点 C = [ x 0 , y 0 , z 0 ] ⊤ \mathrm{C}=\left[x_0, y_0, z_0\right]^{\top} C=[x0,y0,z0]⊤, 确定 3 D 3 \mathrm{D} 3D 空间中的平面 π = [ π x , π y , π z , π w ] ⊤ \pi=\left[\pi_x, \pi_y, \pi_z, \pi_w\right]^{\top} π=[πx,πy,πz,πw]⊤ :
π x ( x − x 0 ) + π y ( y − y 0 ) + π z ( z − z 0 ) = 0 \pi_x\left(x-x_0\right)+\pi_y\left(y-y_0\right)+\pi_z\left(z-z_0\right)=0 πx(x−x0)+πy(y−y0)+πz(z−z0)=0
这里
[ π x π y π z ] = [ s c 1 ] × e c 1 , π w = π x x 0 + π y y 0 + π z z 0 \left[\begin{array}{c} \pi_x \\ \pi_y \\ \pi_z \end{array}\right]=\left[\mathbf{s}^{c_1}\right]_{\times} \mathrm{e}^{c_1}, \quad \pi_w=\pi_x x_0+\pi_y y_0+\pi_z z_0 πxπyπz =[sc1]×ec1,πw=πxx0+πyy0+πzz0
- 这里对偶矩阵的内容可以看《多视图几何》
给定相机坐标系 c 1 c_1 c1 中的两个平面 π 1 \pi_1 π1 和 π 2 \pi_2 π2, 对偶普吕克矩阵 L ∗ \mathrm{L}^* L∗ 可以通过以下方式计算
L ∗ = [ [ d ] x n − n ⊤ 0 ] = π 1 π 2 ⊤ − π 2 π 1 ⊤ ∈ R 4 × 4 \mathbf{L}^*=\left[\begin{array}{cc} {[\mathbf{d}]_{\mathbf{x}}} & \mathbf{n} \\ -\mathbf{n}^{\top} & 0 \end{array}\right]=\pi_1 \pi_2^{\top}-\pi_2 \pi_1^{\top} \in \mathbb{R}^{4 \times 4} L∗=[[d]x−n⊤n0]=π1π2⊤−π2π1⊤∈R4×4
相机坐标系 c 1 c_1 c1 中的 Plücker 坐标 L = ( n T , d T ) T \mathcal{L} =(\mathbf{n}^T,\mathbf{d}^T)^T L=(nT,dT)T很容易从对偶 Plücker 矩阵 L ∗ L^* L∗ 中提取。可以看出, n \mathbf{n} n 和 d \mathrm{d} d 不需要是单位向量。
主体逻辑在void FeatureManager::triangulateLine(Vector3d Ps[], Vector3d tic[], Matrix3d ric[]) 中:
- 根据线段起点终点相机原点求平面:
欧式空间3D平面有3个自由度,对其表示方式主要有两种:Hesse形式、球坐标。
- Hesse形式

π = ( n ⊤ , d ) ⊤ ∈ R 4 \pi=\left(\mathbf{n}^{\top}, d\right)^{\top} \in \mathbb{R}^4 π=(n⊤,d)⊤∈R4
- 球坐标
 $$ \tau=(\theta, \phi, d)^{\top}=q(\pi)=\left(\theta=\arctan \frac{n_y}{n_x}, \phi=\arcsin n_z, d\right)^{\top} $$
$$ \tau=(\theta, \phi, d)^{\top}=q(\pi)=\left(\theta=\arctan \frac{n_y}{n_x}, \phi=\arcsin n_z, d\right)^{\top} $$
一般优化中采用球坐标的表示方式
/*三点确定一个平面 a(x-x0)+b(y-y0)+c(z-z0)=0 --> ax + by + cz + d = 0 d = -(ax0 + by0 + cz0)平面通过点(x0,y0,z0)以及垂直于平面的法线(a,b,c)来得到(a,b,c)^T = vector(AO) cross vector(BO)d = O.dot(cross(AO,BO))*/
Vector4d pi_from_ppp(Vector3d x1, Vector3d x2, Vector3d x3) {Vector4d pi;pi << ( x1 - x3 ).cross( x2 - x3 ), - x3.dot( x1.cross( x2 ) ); // d = - x3.dot( (x1-x3).cross( x2-x3 ) ) = - x3.dot( x1.cross( x2 ) )return pi;
}
如果两平面夹角小于 15 度,不三角化。两个平面求交线,即是进行三角化:
// 两平面相交得到直线的plucker 坐标
Vector6d pipi_plk( Vector4d pi1, Vector4d pi2){Vector6d plk;Matrix4d dp = pi1 * pi2.transpose() - pi2 * pi1.transpose();plk << dp(0,3), dp(1,3), dp(2,3), - dp(1,2), dp(0,2), - dp(0,1);return plk;
}
这里得到的结果实际上是归一化平面坐标系上的三角化结果。
Vector6d plk = pipi_plk(pii, pij);Vector3d n = plk.head(3);Vector3d v = plk.tail(3);// ...plk坐标的矩阵形式Vector3d pc, nc, vc;nc = it_per_id.line_plucker.head(3);vc = it_per_id.line_plucker.tail(3);Matrix4d Lc;Lc << skew_symmetric(nc), vc, -vc.transpose(), 0;- 完整三角化逻辑在这个函数里面。
3.2.正交表示
由于3D空间的直线只有4个自由度,使用Plücker坐标这种过参数化的表示形式在优化的时候不方便,所以我们引入四个参数的正交表示 ( U , W ) ∈ S O ( 3 ) × S O ( 2 ) (\mathbf{U},\mathbf{W}) \in SO(3) \times SO(2) (U,W)∈SO(3)×SO(2) 。Plücker坐标和正交表示之间可以很方便的互相转换,我们之后会分别介绍如何从Plücker坐标到正交表示和正交表示怎么变换成Plücker坐标。首先我们需要知道了直线的Plücker坐标 L = ( n ⊤ , d ⊤ ) ⊤ \cal{L} =(\mathbf{n}^{\top},\mathbf{d}^{\top})^{\top} L=(n⊤,d⊤)⊤ ,然后对 L \cal{L} L 进行QR分解,得到:
[ n d ] = [ n ∥ n ∥ d ∥ d ∥ n × d ∥ n × d ∥ ] [ ∥ n ∥ 0 0 ∥ d ∥ 0 0 ] = U W \left[ \begin{array}{ll}{\mathbf{n}} & {\mathbf{d}}\end{array}\right]=\left[ \begin{array}{ccc}{\frac{\mathbf{n}}{\|\mathbf{n}\|}} & {\frac{\mathbf{d}}{\|\mathbf{d}\|}} & {\frac{\mathbf{n} \times \mathbf{d}}{\|\mathbf{n} \times \mathbf{d}\|}}\end{array}\right] \left[ \begin{array}{cc}{\|\mathbf{n}\|} & {0} \\ {0} & {\|\mathbf{d}\|} \\ {0} & {0}\end{array}\right]= \mathrm{U} \mathrm{W} [nd]=[∥n∥n∥d∥d∥n×d∥n×d] ∥n∥000∥d∥0 =UW
分解得到的第一项是正交矩阵 U \bf{U} U ,是一个旋转矩阵。所表示的是相机坐标系到直线坐标系的旋转。其中直线坐标系的定义如下:用直线的方向向量以及直线和光心组成平面的法向量作为坐标的两个轴,再用他们叉乘得到的向量作为第三个轴,所以
U = R ( ψ ) = [ n ∣ ∣ n ∣ ∣ d ∣ ∣ d ∣ ∣ n × d ∣ ∣ n × d ∣ ∣ ] \mathbf{U}=\mathbf{R}(\boldsymbol{\psi})=\left[ \begin{matrix} \frac{\mathbf{n}}{||\mathbf{n}||} & \frac{\mathbf{d}}{||\mathbf{d}||} & \frac{\mathbf{n}\times\mathbf{d}}{||\mathbf{n}\times\mathbf{d}||} \end{matrix} \right] U=R(ψ)=[∣∣n∣∣n∣∣d∣∣d∣∣n×d∣∣n×d]
其中 ψ = [ ψ 1 , ψ 2 , ψ 3 ] ⊤ \boldsymbol{\psi}=\left[\psi_{1}, \psi_{2}, \psi_{3}\right]^{\top} ψ=[ψ1,ψ2,ψ3]⊤ 代表的是相机坐标系到直线坐标系在 x x x , y y y 和 z z z 轴的旋转角。
到此我们得到了正交表示的第一项,第二项需要做一些小变换。由于将 ( ∣ ∣ n ∣ ∣ , ∣ ∣ d ∣ ∣ ||\mathbf{n}||,||\mathbf{d}|| ∣∣n∣∣,∣∣d∣∣) 结合之后只有一个自由度( W \mathrm{W} W的秩为2),所以我们可以用三角函数矩阵参数化:
W = [ w 1 − w 2 w 2 w 1 ] = [ cos ( ϕ ) − sin ( ϕ ) sin ( ϕ ) cos ( ϕ ) ] = 1 ( ∥ n ∥ 2 + ∥ d ∥ 2 ) [ ∥ n ∥ − ∥ d ∥ ∥ d ∥ ∥ n ∥ ] \begin{array}{c}{\mathbf{W}=\left[\begin{matrix}w_1&-w_2\\w_2&w_1\end{matrix}\right]=\left[ \begin{array}{cc}{\cos (\phi)} & {-\sin (\phi)} \\ {\sin (\phi)} & {\cos (\phi)}\end{array}\right]} \\ {=\frac{1}{\sqrt{\left(\|\mathbf{n}\|^{2}+\|\mathbf{d}\|^{2}\right)}}} {\left[ \begin{array}{cc}{\|\mathbf{n}\|} & {-\|\mathbf{d}\|} \\ {\|\mathbf{d}\|} & {\|\mathbf{n}\|}\end{array}\right]}\end{array} W=[w1w2−w2w1]=[cos(ϕ)sin(ϕ)−sin(ϕ)cos(ϕ)]=(∥n∥2+∥d∥2)1[∥n∥∥d∥−∥d∥∥n∥]
上式中的 ϕ \phi ϕ 是旋转角。由于坐标原点(相机光心)到3D直线的距离是 d = ∣ ∣ n ∣ ∣ ∣ ∣ d ∣ ∣ d = \frac{||\mathbf{n}||}{||\mathbf{d}||} d=∣∣d∣∣∣∣n∣∣ ,所以 W \mathbf{W} W 包含了距离信息 d d d 的。根据 U \mathbf{U} U 和 W \mathbf{W} W 的定义可以看出,4个自由度包括旋转的3个自由度和距离的一个自由度。在优化的时候,我们使用 O = [ ψ , ϕ ] ⊤ \mathcal{O}=[\psi, \phi]^{\top} O=[ψ,ϕ]⊤ 作为空间直线更新的最小表示。
正交表示到Plücker坐标之间的变换可以通过下面的方式计算出来:
L ′ = [ w 1 u 1 T , w 2 u 2 T ] T = 1 ( ∥ n ∥ 2 + ∥ d ∥ 2 ) L \mathcal{L}^{\prime}=\left[w_{1} \mathbf{u}_{1}^{T}, w_{2} \mathbf{u}_{2}^{T}\right]^{T}=\frac{1}{\sqrt{\left(\|\mathbf{n}\|^{2}+\|\mathbf{d}\|^{2}\right)}} \mathcal{L} L′=[w1u1T,w2u2T]T=(∥n∥2+∥d∥2)1L
其中 u i \mathbf{u}_i ui 是矩阵 U \mathbf{U} U 的第 i i i 列、 w 1 = cos ( ϕ ) w_1=\cos (\phi) w1=cos(ϕ) 和 w 2 = sin ( ϕ ) w_2=\sin (\phi) w2=sin(ϕ) 。 L ′ \mathcal{L}^{\prime} L′ 和 L \mathcal{L} L 之间存在比例因子,但它们代表相同的3D空间线。
-
plk转正交表示
Vector4d plk_to_orth(Vector6d plk) {Vector4d orth;Vector3d n = plk.head(3);Vector3d v = plk.tail(3);Vector3d u1 = n / n.norm();Vector3d u2 = v / v.norm();Vector3d u3 = u1.cross(u2);// todo:: use SO3orth[0] = atan2(u2(2), u3(2));orth[1] = asin(-u1(2));orth[2] = atan2(u1(1), u1(0));Vector2d w(n.norm(), v.norm());w = w / w.norm();orth[3] = asin(w(1));return orth; } -
正交表示转plk
Vector6d orth_to_plk(Vector4d orth) {Vector6d plk;Vector3d theta = orth.head(3);double phi = orth[3];double s1 = sin(theta[0]);double c1 = cos(theta[0]);double s2 = sin(theta[1]);double c2 = cos(theta[1]);double s3 = sin(theta[2]);double c3 = cos(theta[2]);Matrix3d R;R << c2 * c3, s1 * s2 * c3 - c1 * s3, c1 * s2 * c3 + s1 * s3, c2 * s3,s1 * s2 * s3 + c1 * c3, c1 * s2 * s3 - s1 * c3, -s2, s1 * c2, c1 * c2;double w1 = cos(phi);double w2 = sin(phi);double d = w1 / w2; // 原点到直线的距离Vector3d u1 = R.col(0);Vector3d u2 = R.col(1);Vector3d n = w1 * u1;Vector3d v = w2 * u2;plk.head(3) = n;plk.tail(3) = v;// Vector3d Q = -R.col(2) * d;// plk.head(3) = Q.cross(v);// plk.tail(3) = v;return plk; }
优化的时候使用正交表示。这部分操作位于line_geometry.h/cpp
4.线段残差对位姿的导数
- 这一小节理论部分来自这里,当然也是来自原论文。
4.1.直线的观测模型和误差
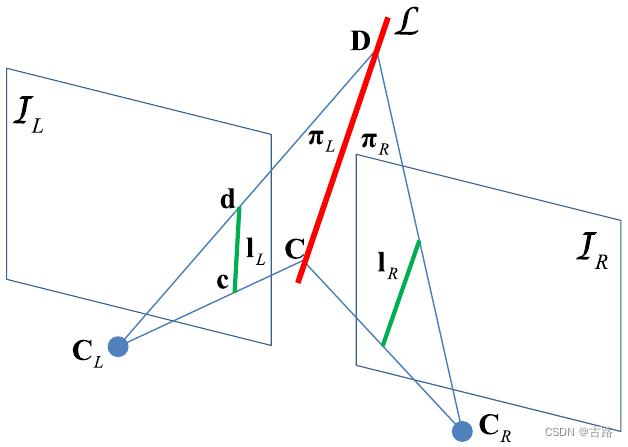
图2 空间直线投影到像素平面
要想知道线特征的观测模型,我们需要知道线特征从归一化平面到像素平面的投影内参矩阵 K \cal{K} K 。如图2,点 C C C 和 D D D 是直线 L = ( n ⊤ , d ⊤ ) ⊤ \mathcal{L} =(\mathbf{n}^{\top},\mathbf{d}^{\top})^{\top} L=(n⊤,d⊤)⊤ 上两点,点 c c c 和 d d d 是它们在像素平面上的投影。 c = K C c = KC c=KC, d = K D d=KD d=KD , K K K是相机的内参矩阵。 n = [ C ] × D , l = [ l 1 l 2 l 3 ] = [ c ] × d \mathbf{n}=[C]_{\times}D ,\mathscr{l} = \left[\begin{matrix}l_1&l_2&l_3\end{matrix}\right]=[c]_{\times}d n=[C]×D,l=[l1l2l3]=[c]×d 。那么有
l = K n = [ f y 0 0 0 f x 0 − f y c x − f x c y f x f y ] n \mathscr{l} = \mathcal{K} \mathbf{n} =\left[ \begin{array}{ccc}{f_{y}} & {0} & {0} \\ {0} & {f_{x}} & {0} \\ {-f_{y} c_{x}} & {-f_{x} c_{y}} & {f_{x} f_{y}}\end{array}\right] \mathbf{n} l=Kn= fy0−fycx0fx−fxcy00fxfy n
l i = c i × d i = ( K C n ) × ( K D n ) = [ f x X C + c x f y Y C + c y 1 ] × [ f x X D + c x f y Y D + c y 1 ] = [ 0 − 1 ( f y Y C + c y ) 1 0 − ( f x X C + c x ) − ( f y Y C + c y ) ( f x X C + c x ) 0 ] [ f x X D + c x f y Y D + c y 1 ] = [ f y ( Y C − Y D ) f x ( X C − X D ) f x f y ( X C Y D − Y C X D ) + f x c y ( X D − X C ) + f y c x ( Y D − Y C ) ] = [ f y 0 0 0 f x 0 − f y c x − f x c y f x f y ] [ Y D − Y C X D − X C X C Y D − Y C X D ] = [ f y 0 0 0 f x 0 − f y c x − f x c y f x f y ] [ X C Y C 1 ] × [ X D Y D 1 ] = K ( C n × D n ) = K n \begin{aligned}{l}^i = c{^i} \times d{^i} &= (KC{^n}) \times (KD{^n}) \\ &=\begin{bmatrix}fxX_C+cx \\ fyY_C+cy \\ 1\end{bmatrix}_{\times}\begin{bmatrix}fxX_D+cx \\ fyY_D+cy \\ 1\end{bmatrix} \\ &=\begin{bmatrix}0 & -1 & (fyY_C+cy) \\ 1 & 0 & -(fxX_C+cx) \\ -(fyY_C+cy) & (fxX_C+cx) & 0 \end{bmatrix}\begin{bmatrix}fxX_D+cx \\ fyY_D+cy \\ 1\end{bmatrix} \\ &=\begin{bmatrix}fy(Y_C-Y_D) \\ fx(X_C-X_D) \\ fxfy(X_CY_D-Y_CX_D)+fxcy(X_D-X_C)+fycx(Y_D-Y_C) \end{bmatrix} \\ &=\begin{bmatrix}fy & 0 & 0 \\ 0 & fx & 0 \\ -fycx & -fxcy & fxfy \end{bmatrix}\begin{bmatrix}Y_D-Y_C \\ X_D-X_C \\ X_CY_D-Y_CX_D \end{bmatrix} \\ &=\begin{bmatrix}fy & 0 & 0 \\ 0 & fx & 0 \\ -fycx & -fxcy & fxfy \end{bmatrix} \begin{bmatrix}X_C \\ Y_C \\ 1 \end{bmatrix}_{\times} \begin{bmatrix}X_D \\ Y_D \\ 1 \end{bmatrix} \\ &=\mathcal{K}(C{^n} \times D{^n}) \\ &=\mathcal{K} \mathbf{n} \end{aligned} li=ci×di=(KCn)×(KDn)= fxXC+cxfyYC+cy1 × fxXD+cxfyYD+cy1 = 01−(fyYC+cy)−10(fxXC+cx)(fyYC+cy)−(fxXC+cx)0 fxXD+cxfyYD+cy1 = fy(YC−YD)fx(XC−XD)fxfy(XCYD−YCXD)+fxcy(XD−XC)+fycx(YD−YC) = fy0−fycx0fx−fxcy00fxfy YD−YCXD−XCXCYD−YCXD = fy0−fycx0fx−fxcy00fxfy XCYC1 × XDYD1 =K(Cn×Dn)=Kn
上式表明,直线的线投影只和法向量有关和方向向量无关。
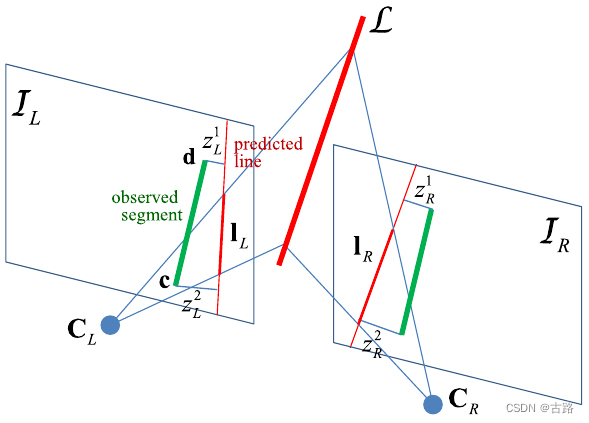
关于投影的误差,我们不可以直接从两幅图像的线段中得到,因为同一条直线在不同图像线段的长度和大小都是不一样的。衡量线的投影误差必须从空间中重投影回当前的图像中才能定义误差。在给定世界坐标系下的空间直线 L l w \mathcal{L}^w_l Llw 和正交表示 O l \mathcal{O}_l Ol ,我们首先使用外参(这也是我们需要优化求解的东西) T c w = [ R c w p c w 0 1 ] T_{cw} = \left[\begin{matrix}R_{cw} & p_{cw}\\0&1 \end{matrix}\right] Tcw=[Rcw0pcw1] 将直线变换到相机归一化平面下的观测 c i c_i ci 坐标下。然后再将直线利用相机内参投影到成像平面上得到投影线段 l l c i \mathscr{l}_l^{c_i} llci ,然后我们就得到了线的投影误差。我们将线的投影误差定义为图像中观测线段的端点到从空间重投影回像素平面的预测直线的距离。
r l ( z L l c i , X ) = [ d ( s l c i , l l c i ) d ( e l c i , l l c i ) ] d ( s , 1 ) = s ⊤ l l 1 2 + l 2 2 \mathbf{r}_{l}\left(\mathbf{z}_{\mathcal{L}_{l}}^{c_{i}}, \mathcal{X}\right)=\left[ \begin{array}{l}{d\left(\mathbf{s}_{l}^{c_{i}}, \mathbf{l}_{l}^{c_{i}}\right)} \\ {d\left(\mathbf{e}_{l}^{c_{i}}, \mathbf{l}_{l}^{c_{i}}\right)}\end{array}\right]\\d(\mathbf{s}, 1)=\frac{\mathbf{s}^{\top} \mathbf{l}}{\sqrt{l_{1}^{2}+l_{2}^{2}}} rl(zLlci,X)=[d(slci,llci)d(elci,llci)]d(s,1)=l12+l22s⊤l
其中 s l c i \mathbf{s}_l^{c_i} slci 和 e l c i \mathbf{e}_l^{c_i} elci 是图像中观测到的线段端点, l l c i \mathbf{l}_l^{c_i} llci 是重投影的预测的直线。
double FeatureManager::reprojection_error( Vector4d obs, Matrix3d Rwc, Vector3d twc, Vector6d line_w ) {double error = 0;Vector3d n_w, d_w;n_w = line_w.head(3);d_w = line_w.tail(3);Vector3d p1, p2;p1 << obs[0], obs[1], 1;p2 << obs[2], obs[3], 1;// 根据外参将line从世界坐标系转到相机归一化平面坐标系Vector6d line_c = plk_from_pose(line_w,Rwc,twc);Vector3d nc = line_c.head(3);double sql = nc.head(2).norm();nc /= sql;error += fabs( nc.dot(p1) );error += fabs( nc.dot(p2) );return error / 2.0;
}
这里误差是归一化平面坐标系的误差,因此观测也应该要求是归一化平面,注意中间有个从像素坐标系到归一化平面坐标系的转换,这里没列出来。
误差求解函数在这里。
这个函数实际上只用在了外点剔除这里,真正的优化误差求解是在优化器那里定义的。而且感觉这里的实现坐标有点问题?
4.2.误差雅克比推导
如果要优化的话,需要知道误差的雅克比矩阵:
线特征在VIO下根据链式求导法则:
J l = ∂ r l ∂ l c i ∂ l c i ∂ L c i [ ∂ L c i ∂ δ x i ∂ L c i ∂ L w ∂ L w ∂ δ O ] \mathbf{J}_{l}=\frac{\partial \mathbf{r}_{l}}{\partial \mathbf{l}^{c_{i}}} \frac{\partial \mathbf{l}^{c_{i}}}{\partial \mathcal{L}^{c_{i}}}\left[\frac{\partial \mathcal{L}^{c_{i}}}{\partial \delta \mathbf{x}^{i}} \quad \frac{\partial \mathcal{L}^{c_{i}}}{\partial \mathcal{L}^{w}} \frac{\partial \mathcal{L}^{w}}{\partial \delta \mathcal{O}}\right] Jl=∂lci∂rl∂Lci∂lci[∂δxi∂Lci∂Lw∂Lci∂δO∂Lw]
其中第一项 ∂ r l ∂ l c i \frac{\partial \mathbf{r}_{l}}{\partial \mathbf{l}^{c_{i}}} ∂lci∂rl ,因为
r l = [ s T l l 1 2 + l 2 2 e T l l 1 2 + l 2 2 ] = [ u s l 1 + v s l 2 l 1 2 + l 2 2 u e l 1 + v e l 2 l 1 2 + l 2 2 ] s = [ u s v s 1 ] e = [ u e v e 1 ] l = [ l 1 l 2 l 3 ] \mathbf{r}_l = \left[ \begin{matrix} \frac{\mathbf{s}^T\mathbf{l} }{\sqrt{l_1^2+l_2^2}} \\ \frac{\mathbf{e}^T\mathbf{l} }{\sqrt{l_1^2+l_2^2}} \end{matrix} \right] = \left[ \begin{matrix} \frac{u_sl_1+v_sl_2 }{\sqrt{l_1^2+l_2^2}} \\ \frac{u_el_1+v_el_2 }{\sqrt{l_1^2+l_2^2}} \end{matrix} \right] \\ \mathbf{s} = \left[\begin{matrix} u_s&v_s&1 \end{matrix} \right] \\ \mathbf{e} = \left[\begin{matrix} u_e&v_e&1 \end{matrix} \right] \\ \mathbf{l} = \left[\begin{matrix} l_1&l_2&l_3 \end{matrix} \right] rl= l12+l22sTll12+l22eTl = l12+l22usl1+vsl2l12+l22uel1+vel2 s=[usvs1]e=[ueve1]l=[l1l2l3]
所以:
∂ r l ∂ l = [ ∂ r 1 ∂ l 1 ∂ r 1 ∂ l 2 ∂ r 1 ∂ l 3 ∂ r 2 ∂ l 1 ∂ r 2 ∂ l 2 ∂ r 2 ∂ l 3 ] = [ − l 1 s l ⊤ l ( l 1 2 + l 2 2 ) ( 3 2 ) + u s ( l 1 2 + l 2 2 ) ( 1 2 ) − l 2 s l ⊤ l ( l 1 2 + l 2 2 ) ( 3 2 ) + v s ( l 1 2 + l 2 2 ) ( 1 2 ) 1 ( l 1 2 + l 2 2 ) ( 1 2 ) − l 1 e l ⊤ l ( l 1 2 + l 2 2 ) ( 3 2 ) + e s ( l 1 2 + l 2 2 ) ( 1 2 ) − l 2 e l ⊤ l ( l 1 2 + l 2 2 ) ( 3 2 ) + v e ( l 1 2 + l 2 2 ) ( 1 2 ) 1 ( l 1 2 + l 2 2 ) ( 1 2 ) ] 2 × 3 \begin{align} \frac{\partial \mathbf{r}_{l}}{\partial \mathbf{l}} &=\left[ \begin{array}{lll}{\frac{\partial r_{1}}{\partial l_{1}}} & {\frac{\partial r_{1}}{\partial l_{2}}} & {\frac{\partial r_{1}}{\partial l_{3}}} \\ {\frac{\partial r_{2}}{\partial l_{1}}} & {\frac{\partial r_{2}}{\partial l_{2}}} & {\frac{\partial r_{2}}{\partial l_{3}}}\end{array}\right] \\&=\left[\begin{matrix} \frac{-l_{1} \mathbf{s}_{l}^{\top} \mathbf{l}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{3}{2}\right)}}+\frac{u_{s}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} & \frac{-l_{2} \mathbf{s}_{l}^{\top} \mathbf{l}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{3}{2}\right)}}+\frac{v_{s}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} & \frac{1}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} \\ \frac{-l_{1} \mathbf{e}_{l}^{\top} \mathbf{l}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{3}{2}\right)}}+\frac{e_{s}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} & \frac{-l_{2} \mathbf{e}_{l}^{\top} \mathbf{l}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{3}{2}\right)}}+\frac{v_{e}}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} & \frac{1}{\left(l_{1}^{2}+l_{2}^{2}\right)^{\left(\frac{1}{2}\right)}} \end{matrix}\right]_{2\times3} \end{align} ∂l∂rl=[∂l1∂r1∂l1∂r2∂l2∂r1∂l2∂r2∂l3∂r1∂l3∂r2]= (l12+l22)(23)−l1sl⊤l+(l12+l22)(21)us(l12+l22)(23)−l1el⊤l+(l12+l22)(21)es(l12+l22)(23)−l2sl⊤l+(l12+l22)(21)vs(l12+l22)(23)−l2el⊤l+(l12+l22)(21)ve(l12+l22)(21)1(l12+l22)(21)1 2×3
第二项 ∂ l c i ∂ L c i \frac{\partial \mathbf{l}^{c_{i}}}{\partial \mathcal{L}^{c_{i}}} ∂Lci∂lci(像素坐标到相机归一化坐标,相差一个映射矩阵) ,因为
l = K n L = [ n d ] \mathbf{l} = \mathcal{K}\mathbf{n} \\ \mathcal{L} = \left[\begin{matrix} \mathbf{n} & \mathbf{d}\end{matrix}\right] l=KnL=[nd]
所以:
∂ l c i ∂ L i c i = [ ∂ l n ∂ l d ] = [ K 0 ] 3 × 6 \begin{align} \frac{\partial \mathrm{l}^{c_{i}}}{\partial \mathcal{L}_{i}^{c_{i}}}&=\left[ \begin{matrix} \frac{\partial \mathbf{l}}{\mathbf{n}} &\frac{\partial \mathbf{l}}{\mathbf{d}} \end{matrix} \right] \\&=\left[ \begin{array}{ll}{\mathcal{K}} & {0}\end{array}\right]_{3 \times 6} \end{align} ∂Lici∂lci=[n∂ld∂l]=[K0]3×6
最后一项矩阵包含两个部分,一个是相机坐标系下线特征对的旋转和平移的误差导数,第二个是直线对正交表示的四个参数增量的导数
第一部分中,
δ x i = [ δ p , δ θ , δ v , δ b a b i , δ b g b i ] \delta \mathbf{x}_{i}=\left[\delta \mathbf{p}, \delta \boldsymbol{\theta}, \delta \mathbf{v}, \delta \mathbf{b}_{a}^{b_{i}}, \delta \mathbf{b}_{g}^{b_{i}}\right] δxi=[δp,δθ,δv,δbabi,δbgbi]
在VIO中,如果要计算线特征的重投影误差,需要将在世界坐标系 w w w 下的线特征变换到IMU坐标系 b b b 下,再用外参数 T b c \bf{T}_{bc} Tbc 变换到相机坐标系 c c c 下。所以
L c = T b c − 1 T w b − 1 L w = T b c − 1 [ R w b ⊤ ( n w + [ d w ] × p w b ) R w b ⊤ d w ] 6 × 1 \begin{aligned} \mathcal{L}_{c} &=\mathcal{T}_{b c}^{-1} \mathcal{T}_{w b}^{-1} \mathcal{L}_{w} \\ &=\mathcal{T}_{b c}^{-1}\left[ \begin{matrix} \mathbf{R}_{w b}^{\top}\left(\mathbf{n}^{w}+\left[\mathbf{d}^{w}\right] \times \mathbf{p}_{wb}\right)\\ \mathbf{R}_{wb}^{\top}\mathbf{d}^w \end{matrix} \right]_{6 \times 1} \end{aligned} Lc=Tbc−1Twb−1Lw=Tbc−1[Rwb⊤(nw+[dw]×pwb)Rwb⊤dw]6×1
其中
T b c = [ R b c [ p b c ] × R b c 0 R b c ] T b c − 1 = [ R b c ⊤ − R b c ⊤ [ p b c ] × 0 R b c ⊤ ] \cal{T}_{bc} = \left[ \begin{array}{cc}{\mathbf{R}_{bc}} & {\left[\mathbf{p}_{bc }\right]_{\times} \mathbf{R}_{bc}} \\ {\mathbf{0}} & {\mathbf{R}_{bc}}\end{array}\right]\\ \cal{T}_{bc}^{-1} = \left[\begin{matrix} \bf{R}_{bc}^{\top} &- \bf{R}_{bc}^{\top} [p_{bc}]_{\times} \\0&\ \bf{R}_{bc}^{\top} \end{matrix}\right] Tbc=[Rbc0[pbc]×RbcRbc]Tbc−1=[Rbc⊤0−Rbc⊤[pbc]× Rbc⊤]
− [ a ] × b = [ b ] × a -[a]_{\times}b=[b]_{\times}a −[a]×b=[b]×a
线特征 L \cal{L} L 只优化状态变量中的位移和旋转,所以只需要对位移和旋转求导,其他都是零。下面我们来具体分析旋转和位移的求导。首先是线特征对旋转的求导:
∂ L c ∂ δ θ b b ′ = T b c − 1 [ ∂ ( I − [ δ θ b b ′ ] × ) R w b ⊤ ( n w + [ d w ] × p w b ) ∂ δ θ b b ′ ] ∂ ( I − [ δ θ b b ′ ] × ⊤ ) R w b ⊤ d w ∂ δ θ b b ′ ] = T b c − 1 [ [ R w b ⊤ ( n w + [ d w ] × p w b ) ] × ] [ R w b ⊤ d w ] × ] 6 × 3 \begin{align} \frac{\partial \mathcal{L}_{c}}{\partial \delta \theta_{b b^{\prime}}} &=\cal{T}_{bc}^{-1}\left[ \begin{array}{c}{\frac{\partial\left(\mathbf{I}-\left[\delta \boldsymbol{\theta}_{b b^{\prime}}\right]_\times\right) \mathbf{R}_{w b}^{\top}\left(\mathbf{n}^{w}+\left[\mathbf{d}^{w}\right]_\times \mathbf{p}_{w b}\right)}{\partial \delta \boldsymbol{\theta}_{b b^{\prime}}} ]} \\ {\frac{\partial\left(\mathbf{I}-\left[\delta \boldsymbol{\theta}_{b b^{\prime}}\right]_{\times}^{\top}\right) \mathbf{R}_{w b}^{\top} \mathbf{d}^{w}}{\partial \delta \boldsymbol{\theta}_{b b^{\prime}}}}\end{array}\right] \\ &=\mathcal{T}_{b c}^{-1} \left[ \begin{array}{c}{\left[\mathbf{R}_{w b}^{\top}\left(\mathbf{n}^{w}+\left[\mathbf{d}^{w}\right]_\times \mathbf{p}_{w b}\right)\right]_\times ]} \\ {\left[\mathbf{R}_{w b}^{\top} \mathbf{d}^{w}\right]_\times}\end{array}\right]_{6 \times 3} \end{align} ∂δθbb′∂Lc=Tbc−1 ∂δθbb′∂(I−[δθbb′]×)Rwb⊤(nw+[dw]×pwb)]∂δθbb′∂(I−[δθbb′]×⊤)Rwb⊤dw =Tbc−1[[Rwb⊤(nw+[dw]×pwb)]×][Rwb⊤dw]×]6×3
然后是线特征对位移的求导:
∂ L c ∂ δ p b b ′ = T b c − 1 [ ∂ R w b ⊤ ( n w + [ d w ] × ( p w b + δ p b b ′ ) ) ∂ δ p b b ′ ∂ R w b ⊤ d w ∂ δ p b b ′ ] = T b c − 1 [ R w b ⊤ [ d w ] × 0 ] 6 × 3 \begin{align} \frac{\partial\cal{L}_c}{\partial\delta \bf{p}_{bb^{\prime}}} &=\mathcal{T}_{b c}^{-1} \left[ \begin{array}{c}{\frac{\partial \mathbf{R}_{w b}^{\top}\left(\mathbf{n}^{w}+\left[\mathbf{d}^{w}\right]_{ \times}\left(\mathbf{p}_{w b}+\delta \mathbf{p}_{b b^{\prime}}\right)\right)}{\partial \delta \mathbf{p}_{b b^{\prime}}}} \\ {\frac{\partial \mathbf{R}_{w b}^{\top} \mathbf{d}^{w}}{\partial \delta \mathbf{p}_{b b^{\prime}}}}\end{array}\right] \\&=\mathcal{T}_{b c}^{-1} \left[ \begin{array}{c}{\mathbf{R}_{w b}^{\top}\left[\mathbf{d}^{w}\right]_{ \times}} \\ {0}\end{array}\right]_{6 \times 3} \end{align} ∂δpbb′∂Lc=Tbc−1 ∂δpbb′∂Rwb⊤(nw+[dw]×(pwb+δpbb′))∂δpbb′∂Rwb⊤dw =Tbc−1[Rwb⊤[dw]×0]6×3
第二部分中 ∂ L c i ∂ L w ∂ L w ∂ δ O \frac{\partial \mathcal{L}^{c_{i}}}{\partial \mathcal{L}^{w}} \frac{\partial \mathcal{L}^{w}}{\partial \delta \mathcal{O}} ∂Lw∂Lci∂δO∂Lw ,先解释第一个 ∂ L c i ∂ L w \frac{\partial \mathcal{L}^{c_{i}}}{\partial \mathcal{L}^{w}} ∂Lw∂Lci
L c = T w c − 1 L w \mathcal{L}^c = \mathcal{T}_{wc}^{-1}\mathcal{L}^w Lc=Twc−1Lw
所以 ∂ L c i ∂ L w = T w c − 1 \frac{\partial\cal{L}^{c_i}}{\partial\cal{L}^w} = \mathcal{T}_{wc}^{-1} ∂Lw∂Lci=Twc−1
然后后面的 ∂ L w ∂ δ O \frac{\partial \mathcal{L}^{w}}{\partial \delta \mathcal{O}} ∂δO∂Lw 有两种思路,先介绍第一种:
∂ L w ∂ δ O = [ ∂ L w ∂ ψ 1 ∂ L w ∂ ψ 2 ∂ L w ∂ ψ 3 ∂ L w ∂ ϕ ] ∂ L w ∂ ψ 1 = ∂ L w ∂ U ∂ U ∂ ψ 1 ∂ L w ∂ ϕ = ∂ L w ∂ w ∂ w ∂ ϕ 1 \frac{\partial \mathcal{L}^{w}}{\partial \delta \mathcal{O}} = \left[\begin{matrix} \frac{\partial\cal{L}^w}{\partial \psi_1} & \frac{\partial\cal{L}^w}{\partial \psi_2} & \frac{\partial\cal{L}^w}{\partial \psi_3} & \frac{\partial\cal{L}^w}{\partial \phi} \end{matrix} \right] \\ \frac{\partial \cal{L}^w}{\partial\psi_1} = \frac{\partial\cal{L}^w}{\partial \bf{U}}\frac{\partial \bf{U}}{\partial\psi_1} \\ \frac{\partial \cal{L}^w}{\partial\phi} = \frac{\partial\cal{L}^w}{\partial \bf{w}}\frac{\partial \bf{w}}{\partial\phi_1} ∂δO∂Lw=[∂ψ1∂Lw∂ψ2∂Lw∂ψ3∂Lw∂ϕ∂Lw]∂ψ1∂Lw=∂U∂Lw∂ψ1∂U∂ϕ∂Lw=∂w∂Lw∂ϕ1∂w
其中 L \cal{L} L 对 U \bf{U} U 和 w = [ w 1 , w 2 ] \mathbf{w}=[w_1,w_2] w=[w1,w2] 求导,因为 L w = [ w 1 u 1 ⊤ w 2 u 2 ⊤ ] ⊤ \mathcal{L}^w = \left[ \begin{matrix} w_1\bf{u}^{\top}_1&w_2\bf{u}^{\top}_2 \end{matrix}\right]^{\top} Lw=[w1u1⊤w2u2⊤]⊤ ,所以
∂ L ∂ U = [ ∂ L ∂ U 1 ∂ L ∂ U 2 ∂ L ∂ U 3 ] 6 × 9 = [ w 1 ( 3 × 3 ) 0 0 0 w 2 ( 3 × 3 ) 0 ] \begin{align} \frac{\partial\cal{L}}{\partial\bf{U}} &= \left[\begin{matrix} \frac{\partial\cal{L}}{\partial\bf{U}_1} & \frac{\partial\cal{L}}{\partial\bf{U}_2} & \frac{\partial\cal{L}}{\partial\bf{U}_3} \end{matrix}\right]_{6\times9} \\ &=\left[\begin{matrix} w_{1(3\times3)}&0&0\\0&w_{2(3\times3)}&0\end{matrix}\right] \end{align} ∂U∂L=[∂U1∂L∂U2∂L∂U3∂L]6×9=[w1(3×3)00w2(3×3)00]
∂ L ∂ w = [ ∂ L ∂ w 1 ∂ L ∂ w 2 ] 6 × 2 = [ u 1 0 0 u 2 ] \begin{align} \frac{\partial\cal{L}}{\partial\bf{w}} &= \left[\begin{matrix} \frac{\partial\cal{L}}{\partial w_1} & \frac{\partial\cal{L}}{\partial w_2} \end{matrix}\right]_{6\times2} \\ &=\left[\begin{matrix}\bf{u}_1&0 \\0&\bf{u}_2 \end{matrix}\right] \end{align} ∂w∂L=[∂w1∂L∂w2∂L]6×2=[u100u2]
然后是 U \bf{U} U 对 ψ \psi ψ 和 W \bf{W} W 对 ϕ \phi ϕ 的求导,
因为 U ′ ≈ U ( I + [ δ ψ ] × ) \begin{aligned} \mathbf{U}^{\prime} & \approx \mathbf{U}\left(\mathbf{I}+[\delta \psi]_{ \times}\right) \end{aligned} U′≈U(I+[δψ]×) ,所以
[ u 1 u 2 u 3 ] ′ = [ u 1 u 2 u 3 ] + [ u 1 u 2 u 3 ] × δ ψ [ u 1 u 2 u 3 ] ′ − [ u 1 u 2 u 3 ] δ ψ = [ u 1 u 2 u 3 ] × ∂ U ∂ ψ 1 = [ 0 u 3 − u 2 ] ∂ U ∂ ψ 2 = [ − u 3 0 u 1 ] ∂ U ∂ ψ 1 = [ u 2 − u 1 0 ] ∂ w ∂ ϕ = [ − w 2 w 1 ] \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right]^{\prime} = \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right] + \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right]_{\times}\delta\psi \\\frac{ \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right]^{\prime} - \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right]}{\delta\psi} = \left[\begin{matrix} \bf{u}_1&\bf{u}_2 & \bf{u}_3 \end{matrix}\right]_{\times}\\ \frac{\partial\bf{U}}{\partial\psi_1} = \left[\begin{matrix} 0&\bf{u}_3 & -\bf{u}_2 \end{matrix}\right]\\ \frac{\partial\bf{U}}{\partial\psi_2} = \left[\begin{matrix} -\bf{u}_3&0 & \bf{u}_1 \end{matrix}\right]\\ \frac{\partial\bf{U}}{\partial\psi_1} = \left[\begin{matrix} \bf{u}_2 & -\bf{u}_1&0 \end{matrix}\right]\\ \frac{\partial\bf{w}}{\partial\phi} = \left[\begin{matrix} -w_2\\w_1 \end{matrix}\right] [u1u2u3]′=[u1u2u3]+[u1u2u3]×δψδψ[u1u2u3]′−[u1u2u3]=[u1u2u3]×∂ψ1∂U=[0u3−u2]∂ψ2∂U=[−u30u1]∂ψ1∂U=[u2−u10]∂ϕ∂w=[−w2w1]
所以,可得
∂ L w ∂ δ O = [ ∂ L w ∂ ψ 1 ∂ L w ∂ ψ 2 ∂ L w ∂ ψ 3 ∂ L w ∂ ϕ ] = [ ∂ L w ∂ U ∂ U ∂ ψ 1 ∂ L w ∂ U ∂ U ∂ ψ 2 ∂ L w ∂ U ∂ U ∂ ψ 3 ∂ L w ∂ w ∂ w ∂ ϕ ] = [ 0 − w 1 u 3 w 1 u 2 − w 2 u 1 w 2 u 3 0 − w 2 u 1 w 1 u 2 ] 6 × 4 \begin{align} \frac{\partial \mathcal{L}^{w}}{\partial \delta \mathcal{O}} &= \left[\begin{matrix} \frac{\partial\cal{L}^w}{\partial \psi_1} & \frac{\partial\cal{L}^w}{\partial \psi_2} & \frac{\partial\cal{L}^w}{\partial \psi_3} & \frac{\partial\cal{L}^w}{\partial \phi} \end{matrix} \right] \\ &= \left[\begin{matrix} \frac{\partial\cal{L}^w}{\partial\bf{U}}\frac{\partial\bf{U}}{\partial \psi_1} & \frac{\partial\cal{L}^w}{\partial\bf{U}}\frac{\partial\bf{U}}{\partial \psi_2} & \frac{\partial\cal{L}^w}{\partial\bf{U}}\frac{\partial\bf{U}}{\partial \psi_3} & \frac{\partial\cal{L}^w}{\partial \bf{w}}\frac{\partial \bf{w}}{\partial \phi} \end{matrix} \right] \\ &=\left[\begin{matrix}0&-w_1\bf{u}_3&w_1\bf{u}_2&-w_2\bf{u}_1\\w_2\bf{u}_3 &0&-w_2\bf{u}_1&w_1\bf{u}_2 \end{matrix} \right]_{6\times4} \end{align} ∂δO∂Lw=[∂ψ1∂Lw∂ψ2∂Lw∂ψ3∂Lw∂ϕ∂Lw]=[∂U∂Lw∂ψ1∂U∂U∂Lw∂ψ2∂U∂U∂Lw∂ψ3∂U∂w∂Lw∂ϕ∂w]=[0w2u3−w1u30w1u2−w2u1−w2u1w1u2]6×4
这篇关于pl_vio线特征·part I的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







