今天分享一道很简单的算法题。
题目来源于 LeetCode 上第 268 号问题:缺失数字。题目难度为 Easy,目前通过率为 50.2% 。
题目描述
给定一个包含 0, 1, 2, ..., n 中 n 个数的序列,找出 0 .. n 中没有出现在序列中的那个数。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
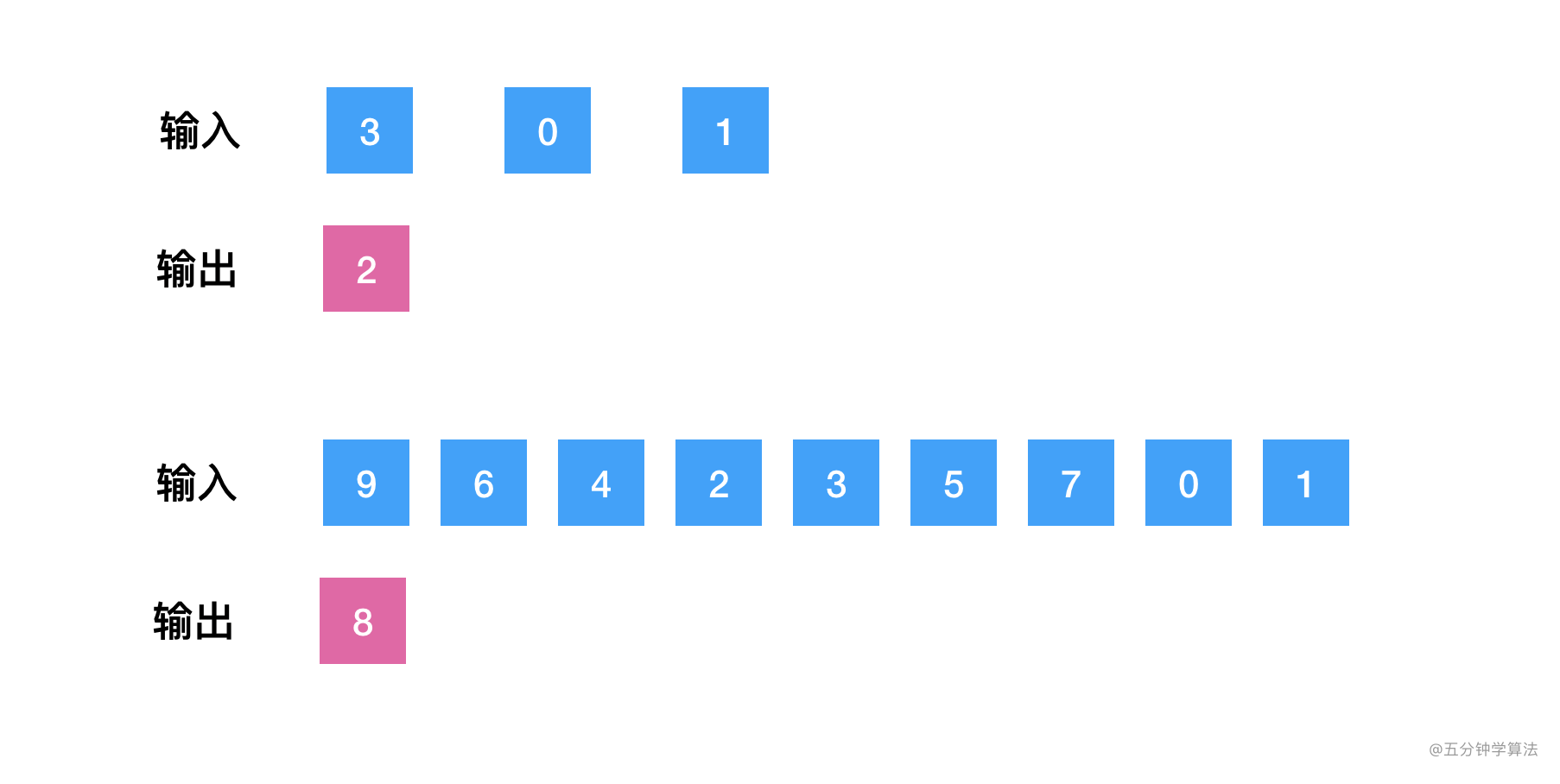
题目解析
这道题目有三种解法。
解法一:异或法
和之前那道 只出现一次的数字 很类似:
只出现一次的数字: 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
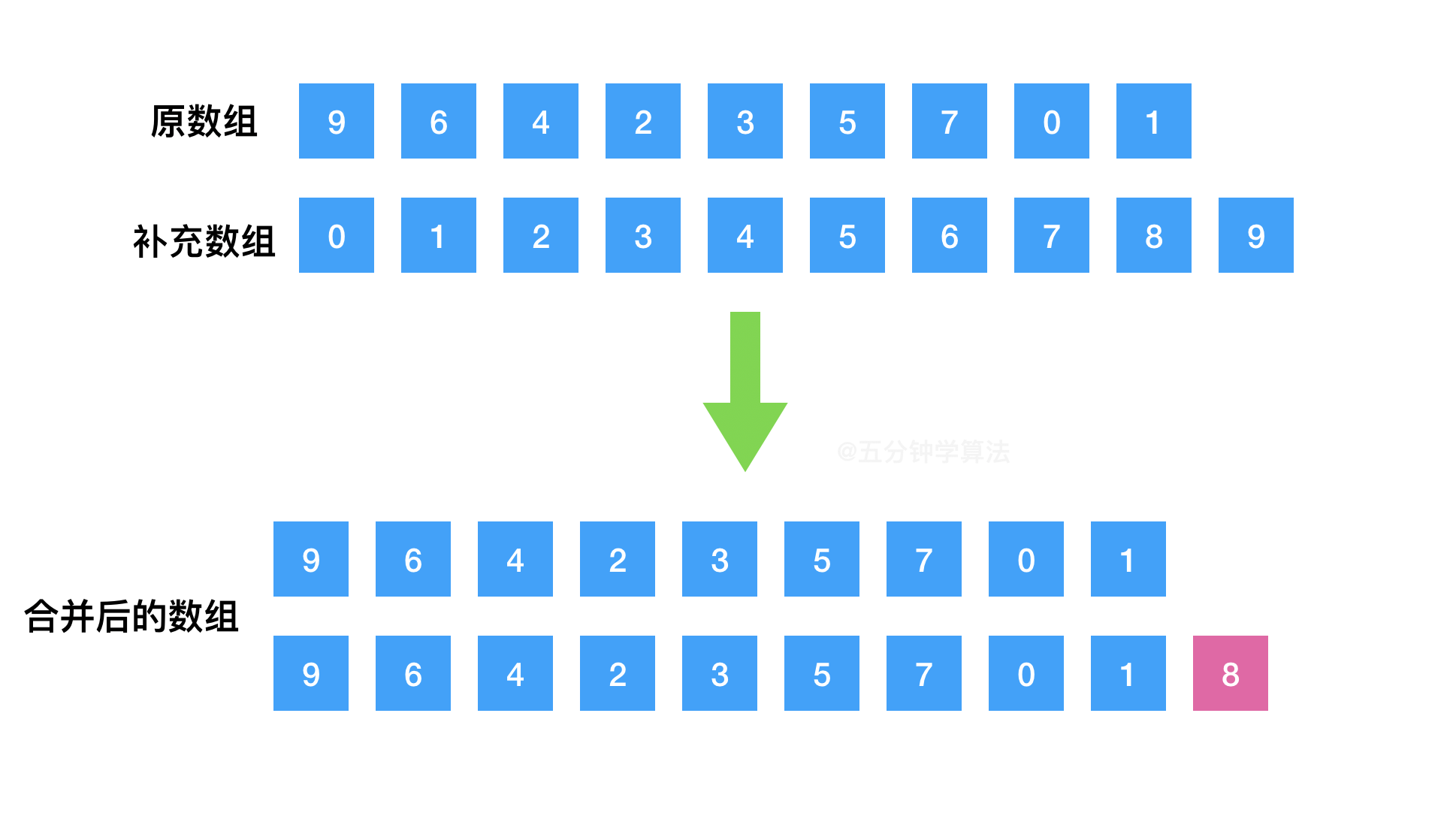
如果我们补充一个完整的数组和原数组进行组合,那所求解的问题就变成了 只出现一次的数字。
将少了一个数的数组与 0 到 n 之间完整的那个数组进行异或处理,因为相同的数字异或会变为了 0 ,那么全部数字异或后,剩下的就是少了的那个数字。
代码实现1
class Solution {
public int missingNumber(int[] nums) {
int res = 0;
//注意数组越界情况
for (int i = 0; i < nums.length;i++){
// i 表示完整数组中的数字,与原数组中的数字 nums[i] 进行异或,再与保存的结果异或
res = res^i^nums[i];
}
//最后需要与循环中无法使用到的那个最大的数异或
return res^i;
}
}
代码实现2
class Solution {
public int missingNumber(int[] nums) {
int res = nums.length;
for (int i = 0; i < nums.length; ++i){
res ^= nums[i];
res ^= i;
}
return res;
}
}
解法二:求和法
- 求出 0 到 n 之间所有的数字之和
- 遍历数组计算出原始数组中数字的累积和
- 两和相减,差值就是丢失的那个数字

//小吴之前担心会数据溢出,不过估计这题考察的不是这个,所以测试用例没写这种吧,还是能 AC 的
class Solution {
public int missingNumber(int[] nums) {
int n = nums.length;
int sum = (n+0)*(n+1)/2;
for (int i=0; i<n; i++){
sum -= nums[i];
}
return sum;
}
}
解法三:二分法
将数组进行排序后,利用二分查找的方法来找到缺少的数字,注意搜索的范围为 0 到 n 。
- 首先对数组进行排序
- 用元素值和下标值之间做对比,如果元素值大于下标值,则说明缺失的数字在左边,此时将 right 赋为 mid ,反之则将 left 赋为 mid + 1 。
注:由于一开始进行了排序操作,因此使用二分法的性能是不如上面两种方法。
public class Solution {
public int missingNumber(int[] nums) {
Arrays.sort(nums);
int left = 0;
int right = nums.length;
while (left < right){
int mid = (left + right) / 2;
if (nums[mid] > mid){
right = mid;
}else{
left = mid + 1;
}
}
return left;
}
}
本文首发于公众号「五分钟学算法」,是图解 LeetCode 系列文章之一。
个人网站:https://www.cxyxiaowu.com







