中点画线算法-Python实现

中点画线算法原理

该方法的主要原理是通过直线的标准方程f(x,y) = Ax+By+C ,若点(x,y)带入方程中，即f(x,y)>0则点在直线上方，小于0则在直线下方。所以在直线斜率属于(0,1)时，下一个渲染的像素点不是y就是y+1，所以我们只需计算f(x+1,y+0.5)的值d与0作比较则可以计算出下一个点的选择，若点(x+1,y+0.5)在直线下方则绘制点(x+1,y+1),否则绘制(x+1,y)。

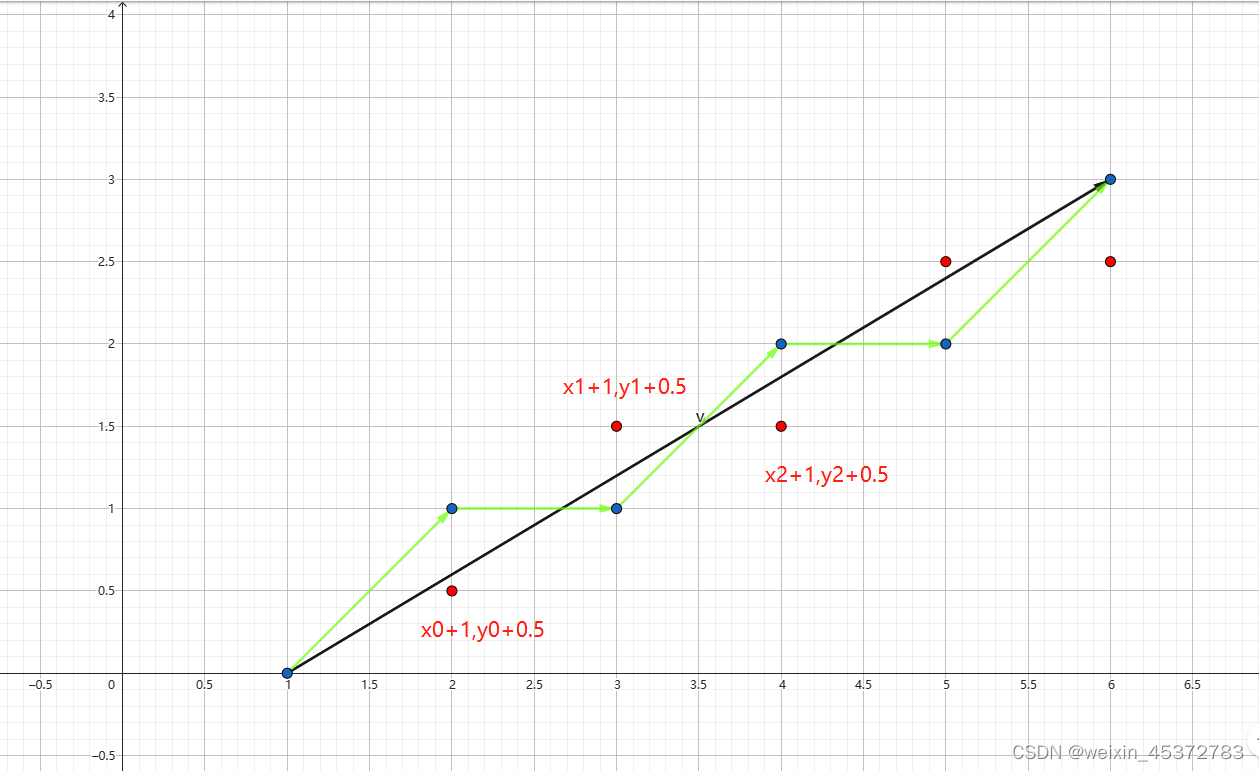
设d=f(x+1,y+0.5)，归纳有di = d(i-1) + A (d>0),di = d(i-1)+ A+B。d0 = A+0.5B。再通过python的matplotlib包绘制点。
推导过程可参考中点画线算法详解。

处理斜率绝对值大于1和斜率小于0的情况，初学方便理解我全部将直线以y=x轴或x=0轴进行翻转得到斜率在（0,1）范围内的情况进行处理，然后再进行翻转回去

python实现

	import matplotlib.pyplot as pltdef Midpoint(self,x1,y1,x2,y2):""""处理斜率绝对值小于一的情况时进行x=y轴翻转处理斜率小于0时，进行x = 0轴的翻转以上处理之后保证变换后的直线在第一象限且斜率在(0,1)内"""t1,t2 = 0,0k = (y2-y1)/(x2-x1)if k < 0 : #若斜率小于0则以y轴翻转,以t2作为标记x1,x2 = -x2,-x1y1,y2 = y2,y1t2 = 1if abs(k) > 1 :#若斜率大于一则x,y轴互换以t1作为标记x1,y1 = y1,x1x2,y2 = y2,x2t1 = 1A = abs(y2 - y1) * -1 #约定直线方程为Ax+By+C = 0，其中A小于0，B大于0，上面变换的操作已经确定A<BB = abs(x2 - x1)d = [A+0.5*B]#d0y = [min(y1,y2)]#y为y1或y2小的那一点先入y轴数组x = [i for i in range(min(x1,x2),max(x1,x2)+1)]#x轴数组for i in range(1,len(x)):if d[i-1] >= 0 :#若d(i-1)大于0，说明上一个中点在直线上方，直线离下边的点近，y不用加1y.append(y[i-1])d.append(d[i-1]+A)else:y.append(y[i-1]+1)#d(i-1)<0，说明上一个中点在直线下方，Y+1d.append(d[i-1]+A+B)if t1 == 1: #以x=y进行翻转x,y = y,xif t2 == 1: #以x = 0 进行翻转x = list(map(lambda x:x*-1,x))r = []# for i in range(len(x)):#     r.append((x[i],y[i]))plt.plot(x,y,linestyle=':', linewidth=1, marker='.', markersize=10, color = 'r')#绘制plt.show()return

运行截图

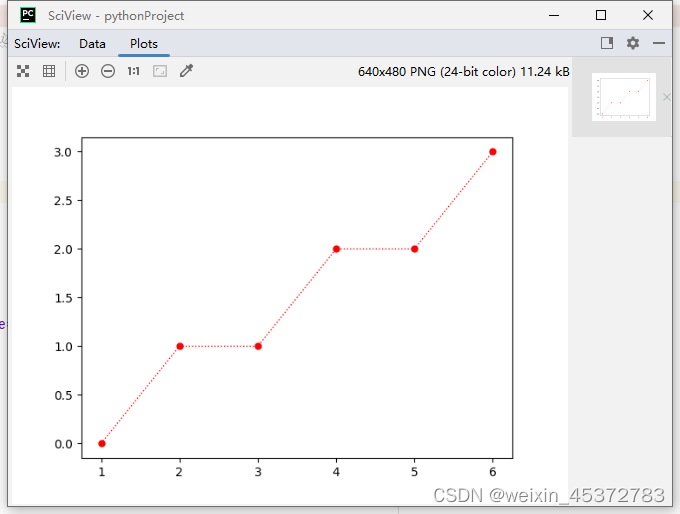
总结

网络上很少有Python写的计算机图形学的算法，现在正好学到当做复习了。
用Python实现相关的图形学算法的博客少也可以理解，毕竟python是解释型语言虽然其封装的很多类与方法使用起来是非得方便的，但是相较于C语言来说python的效率是比较低下的，而且是难以优化的。比如说该算法中其中A,B的值是取整了的，在C语言中整型运算是非常快的，但是在Python中无论是整型还是浮点型都是number类，统一是当做浮点型进行计算相对较慢。当数据量庞大时与c的效率将会体现的更明显。
在上述处理斜率非(0,1)时，我用了“对称翻转”，“旋转”的方法，在这个方法中我是将点存入数组中再进行处理的，对数组的操作也是比较费时的。