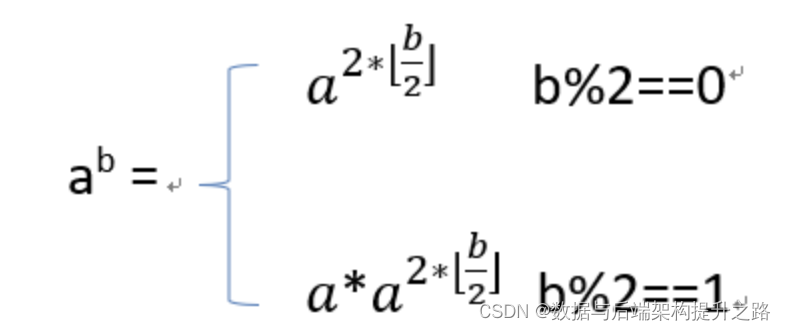LeetCode2961双模幂运算(相关话题:快速幂)

本文主要是介绍LeetCode2961双模幂运算(相关话题:快速幂)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

给你一个下标从 0 开始的二维数组 variables ，其中 variables[i] = [ai, bi, ci, mi]，以及一个整数 target 。

如果满足以下公式，则下标 i 是 好下标：

返回一个由 好下标 组成的数组，顺序不限 。

示例：

输入：variables = [[2,3,3,10],[3,3,3,1],[6,1,1,4]], target = 2
输出：[0,2]

算法思想

Python解法

class Solution:def getGoodIndices(self, variables: List[List[int]], target: int) -> List[int]:return [i for i, (a, b, c, m) in enumerate(variables)if pow(pow(a, b, 10), c, m) == target]

Java解法

public class Solution {public List<Integer> getGoodIndices(int[][] variables, int target) {List<Integer> ans = new ArrayList<>();for (int i = 0; i < variables.length; i++) {int[] v = variables[i];if (pow(pow(v[0], v[1], 10), v[2], v[3]) == target) {ans.add(i);}}return ans;}private long pow(long x, int n, int mod) {long res = 1;for (; n > 0; n /= 2) {if (n % 2 > 0)res = res * x % mod;x = x * x % mod;}return res;}
}

速幂算法是一种高效计算幂运算的方法，尤其适用于大数的情况。下面我将解释这段代码的工作原理：

初始化 res 为 1：res 是最终结果，初始为 1，因为任何数的 0 次幂都是 1。
循环条件 n > 0：算法通过不断将 n 除以 2 来减少计算量。每次迭代后，n 都会减半，直到 n 为 0。这是因为幂运算可以通过二分的方式快速计算。
检查 n % 2 > 0：这个条件用来检查 n 是否为奇数。如果 n 是奇数，我们需要将当前的 x 乘入 res。这是因为当 n 是奇数时，我们不能仅通过平方来得到 x^n，还需要额外乘以一个 x。
更新 res：当 n 是奇数时，res 乘以当前的 x 并对 mod 取模。
平方 x：无论 n 的当前值是奇数还是偶数，都需要将 x 平方，并对 mod 取模，以便下一次迭代使用。
减少 n：通过 n /= 2 减少 n 的值，以进行下一轮迭代。