Regularization——正则化

本文主要是介绍Regularization——正则化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.过拟合问题

这是使用不同的模型根据房子的大小对于房价的预测

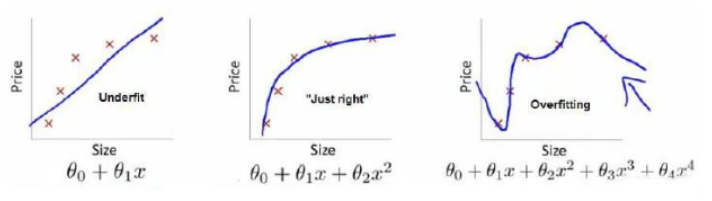
第一张图的模型距离数据点的平均距离仍然比较大，拟合效果并不是特别好，也叫欠拟合（underfitting）

第二张图的模型对于训练集数据的拟合的不错，也能预测数据的趋势，这是我们需要的模型

第三张图的模型拐来拐去，甚至的拟合了训练集的每一个数据点，损失函数接近于0，但如果给一个新的数据，它的效果是很差的，这种模型是过拟合（overfitting）的。可能会疑惑难道这不是最好的模型吗，但评判一个模型的优劣在于其泛化能力，也就是对于新的模型没见过的数据的预测能力，因为这必然是和训练集不一样的。

在分类问题中也存在此问题

欠拟合：泛化能力差，训练样本集准确率低，测试样本集准确率低。
过拟合：泛化能力差，训练样本集准确率高，测试样本集准确率低。
合适的拟合程度：泛化能力强，训练样本集准确率高，测试样本集准确率高

如果我们使用更多特征让模型去学习，模型的参数也就越多，则模型也就会越复杂，过拟合的问题也会越容易产生。

如何解决过拟合：

1.减少特征的数量

人为选择保留重要的特征
使用特征选择算法（PCA）

2.正则化

正则化会保留所有的特征，但通过添加惩罚项来限制参数的大小

2. 正则化

这里介绍正则化也叫L2 regularization

2.1 修改损失函数

上例产生过拟合的模型是

我们可以发现正是高次项让模型产生过拟合，所以如果我们能够让那些高次项的系数接近于0的话，就能够减轻过拟合现象。

回顾线性回归损失函数

$min_{\theta }J(\theta )=min_{\theta }\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x)^{i}-y)^{2}$

如果我们修改成下面这样

让后面两项（也叫惩罚项）也加入损失函数，1000的系数会让我们在最小化损失函数的时候 $\theta _{3}\theta _{4}$ 取值变小，这时候 $\theta _{3}\theta _{4}$ 对结果的影响就会大大降低

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让损失函数最优化过程中自动来选择对这些系数的惩罚的程度

于是这就是线性回归加入惩罚项的模型

（不会对 $\theta _{0}$ 进行惩罚）

范数形式

其中

其中 $\lambda$ 又被称为正则化参数，（同学习率一样是一个超参数（hyper-parameters），需要手动设置）。加入惩罚项后对比效果如下图，可以看到过拟合现象有效缓解

如果我们令 $\lambda$ 的值很大的话，为了使损失函数尽可能的小，所有的 $\theta$ 的值（不包括 $\theta _{0}$ ）都会在一定程度上减小。

如果 $\lambda$ 取值过于大的话，那么除了 $\theta _{0}$ 之外的所有参数都趋近于0，模型接近一条直线，此时不会过拟合了，但反而会欠拟合，损失值一直会很大，梯度下降算法难以收敛。

2.2 惩罚项运行的机理

加入惩罚项后损失函数会分成两个部分

第一部分和之前一样去更好的拟合数据集，

第二部分限制参数的大小，让模型变得更简单

两者相互平衡，从而达到一种相互制约的关系，最终找到一个平衡点，从而在更好地拟合训练集的同时具有良好的泛化能力。

2.3 在线性回归中使用正则化

2.3.1 模型

加入惩罚项的模型在上面已经给出

2.3.2 梯度下降

此时梯度会稍有不同

$\frac{\delta J(\theta )}{\delta \theta }=\frac{1}{m}\sum_{m}^{i=1}(h_{\theta }(x^{i}-y^{i})x^{i})+\frac{1}{m}\lambda\sum_{j=1}^{n}\theta_{j}$

更新参数

$\lambda$ 取值常常小于m，因此

对比一下未加入惩罚项的

$\theta$ 会每次基础上减少了一个额外的值

从另一个方面理解相互制约：

当模型过拟合时，会接近0，即接近于0， $\theta$ 会比较大，此时梯度会消失，随着迭代的继续，一项仍在继续减小着 $\theta$ 的值，随着 $\theta$ 的减小，值会逐渐变大，梯度又会重新出现

2.3.3 正规方程正则化

原本求解 $\theta$

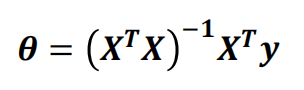
加入正则化后

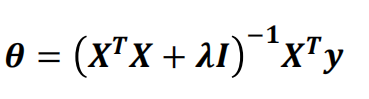，其中I为单位矩阵

此时不会出现不可逆的现象

2.4 在逻辑回归中使用正则化

2.4.1 模型

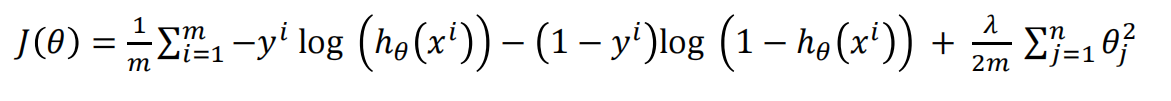
2.4.2 梯度下降

3.正则化实例

ex2data2.txt数据集前两列为特征，最后一列为类标签（1/0）

1.读取数据

data = pd.read_csv('ex2data2.txt',names=['feature1','feature2','label'])
data.head()

2.数据预处理

X = data.iloc[:,0:-1].values
y = data.iloc[:,-1].values
y.reshape(y.shape[0],1)
# 生成特征多项式，最高次为4次方
poly = PolynomialFeatures(degree=4)
X = poly.fit_transform(X)
# 8:2划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

3.模型训练

未使用正则化

model = LogisticRegression(penalty=None,max_iter=1000)
model.fit(X_train, y_train)
y_train_pred = model.predict(X_train)
train_accuracy = accuracy_score(y_train, y_train_pred)
print("train Acc without regularization:",train_accuracy)
y_test_pred = model.predict(X_test)
test_accuracy = accuracy_score(y_test, y_test_pred)
print("test Acc without regularization:",test_accuracy)

使用l2正则化，C为λ的倒数（0-1），故C越小，正则化强度越高

model_l2 = LogisticRegression(penalty='l2',max_iter=1000,C=0.7)
model_l2.fit(X_train, y_train)
y_train_pred = model_l2.predict(X_train)
train_accuracy = accuracy_score(y_train, y_train_pred)
print("train Acc with regularization:",train_accuracy)
y_test_pred = model_l2.predict(X_test)
test_accuracy = accuracy_score(y_test, y_test_pred)
print("test Acc with regularization:",test_accuracy)