本文主要是介绍silent 2020CSP-J初赛试题 改正,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近快要初赛了,刷了2020的试题,发现今年做的还不如去年成绩高,太过于差劲,特别是组合数部分,全错,所以本文把组合数的题解全部详细的写一遍
第十题
五个小朋友并排站成一列,其中有两个小朋友是双胞胎,如果要求这两个双胞胎必须相邻,则有( )种不同排列方法?
五个小朋友,可以划分成两个部分,一个部分是一对双胞胎,一个部分是三个普通小朋友,双胞胎有两个人,所以排列时,第一个人的选择有两种,我们选出了其中一个人作为第一个人,那么就只剩下了一个人所以第二个人的选择只有一种,排列方法有2 * 1种,三个人的如法炮制,3 * 2 * 1种,但是,总排列数并不是2 * 6,因为双胞胎的位置可以变化,五个人中,双胞胎可以站在12,23,34,45这四个位置,剩下三个空让三个普通小朋友用他们的六种方法去填,所以总排列数有2 * 6 * 4=48种
第十四题
10 个三好学生名额分配到 7 个班级,每个班级至少有一个名额,一共有( )种不同的分配方案。
因为每个班都至少要一个名额,所以就干脆让问题变成,三个名额分配给七个班级的问题(将七个名额先均分给七个班级),这三个名额可以玩出三种花样,分别是拆成1 1 1和2 1和不拆,直接把3个名额给一个班,现在我们要考虑一个问题,名额是不具备独特性的,它不像人,所以我们该怎么分呢,3个名额很简单,只能分给一个班,有七种分法,那2 1呢,首先把 2 分给一班,然后1分给二或三或四或五或六或七班,六种分法,然后把2分给2班,1分给三或四或五或六或七班,五种分法,如此类推,则为6+5+4+3+2+1=21种,把1和2的位置颠倒,就又有21种分法,故而是42种分法接下来是1 1 1,照分析2 1的分法,我们能知道有5+4+3+2+1加4+3+2+1加3+2+1加2+1加1也就是35种分法,将42+35+7就是84种分法,这题当然也可以用数学公式做,第十题也一样可以,利用组合数
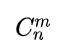
这就是它的形式,意思为,在n中取m个出来的方法有多少个,它的计算公式为
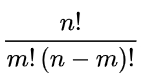
不知道你们怎么想的,但是我看到这个公式确实是一点去算的欲望都没有,毕竟是阶乘级别的算法,当然如果把固定数字的阶乘是多少背下来那自然很好做,比我上面写的方法快多了
十五题
有五副不同颜色的手套(共 10 只手套,每副手套左右手各 1 只),一次性从中取 6 只手套,请问恰好能配成两副手套的不同取法有( )种。
这题比较特殊,因为左右手并且恰好的原因,两副手套如果选了左手那右手也要选,另外的两只手套,拿了左手不能拿右手,所以取两副手套的时候,把手套看成整体,跟十四题的2 1取法类似,但是不能1 2这样,毕竟手套就是手套,不是数字,所以有4+3+2+1种取法,利用组合数,c2 5也是10,但是取另外两只手套的时候,必须看把单个看作成体,因为拿了两副,所以还剩六个手套,但是这六个手套呢,取了第一个,就只有四种选择,如果选了第二个那就是三副手套了,所以这么推,一共有4+4+2+2种取法,那么10*12就是最终答案
感谢观看
这篇关于silent 2020CSP-J初赛试题 改正的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!