本文主要是介绍12.14_黑马数据结构与算法笔记Java,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
120 二叉搜索树 min max
121 二叉搜索树 put
122 二叉搜索树 前任后任1
123 二叉搜索树 前任后任2
124 二叉搜索树 删除1
125 二叉搜索树 删除2
126 二叉搜索树 删除3
127 二叉搜索树 删除 递归1
128 二叉搜索树 删除 递归2
129 二叉搜索树 范围查询
130 二叉搜索树 e01-e03 删增查
131 二叉搜索树 e04 判断合法 中序非递归
132 二叉搜索树 e04 判断合法 中序递归1
133 二叉搜索树 e04 判断合法 中序递归2
134 二叉搜索树 e04 判断合法 上下界
135 二叉搜索树 e05 求范围和
136 二叉搜索树 e06 根据前序遍历结果建树1
137 二叉搜索树 e06 根据前序遍历结果建树2
138 二叉搜索树 e06 根据前序遍历结果建树3
139 二叉搜索树 e07 最近公共祖先
140 avl树 概述
141 avl树 高度和平衡因子
142 avl 四种失衡情况
143 avl 旋转
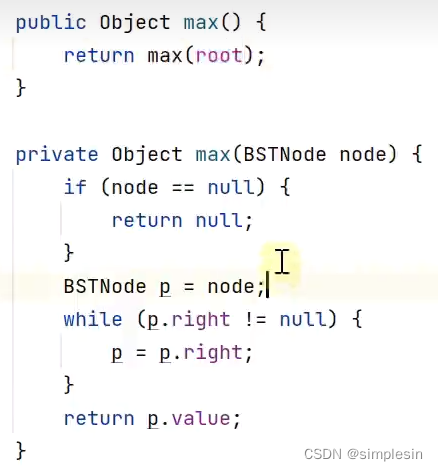
120 二叉搜索树 min max
递归代码

非递归代码


121 二叉搜索树 put
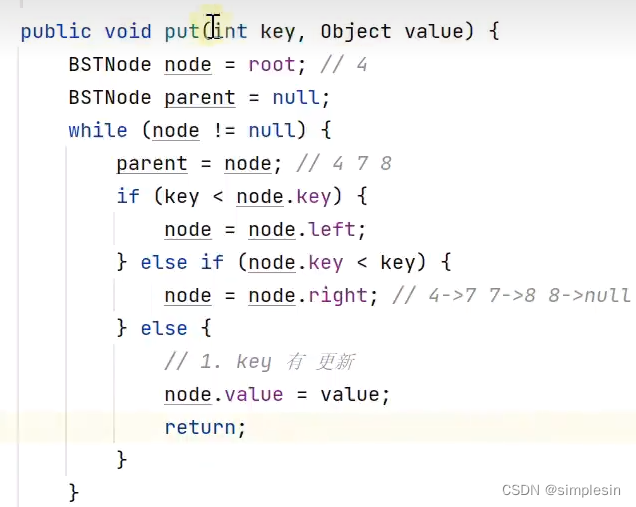

122 二叉搜索树 前任后任1

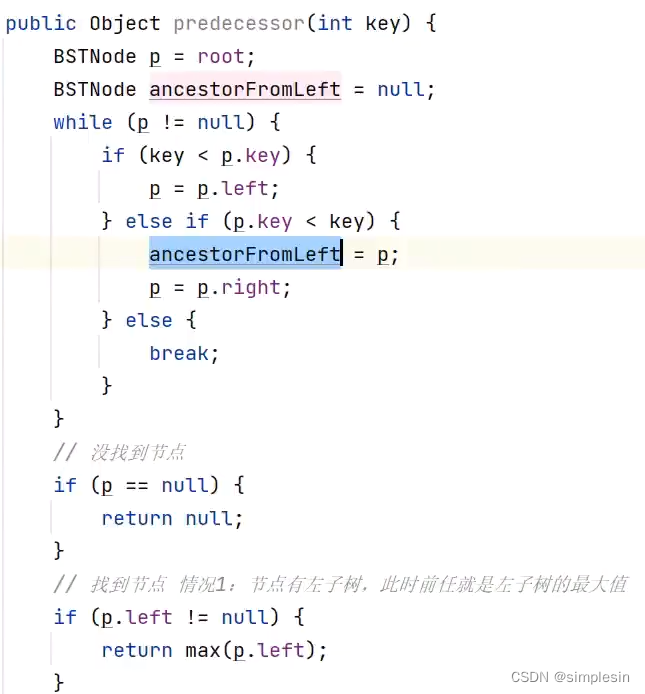

123 二叉搜索树 前任后任2


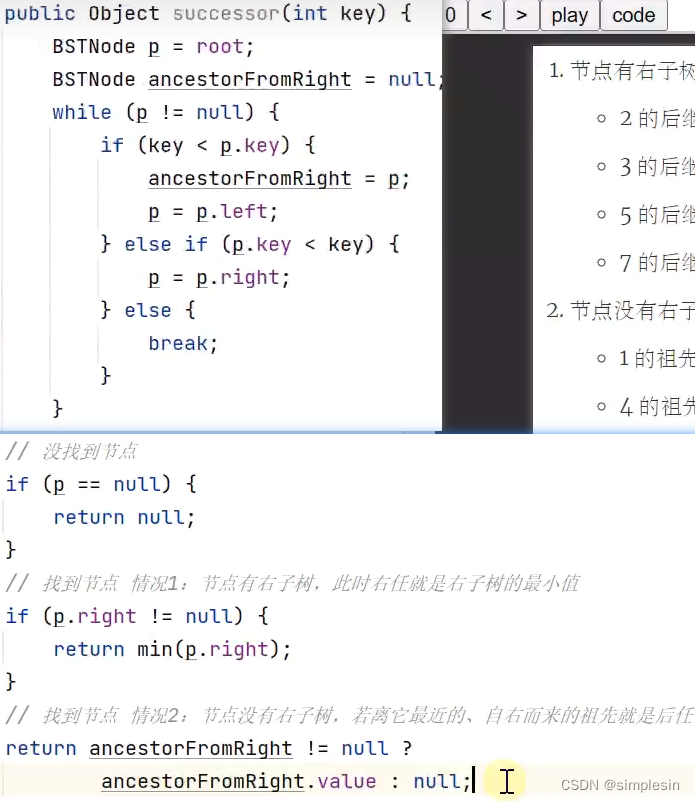
124 二叉搜索树 删除1


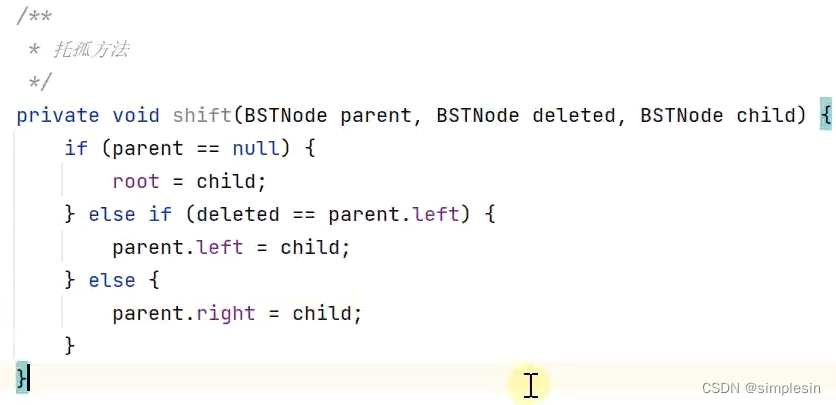
125 二叉搜索树 删除2
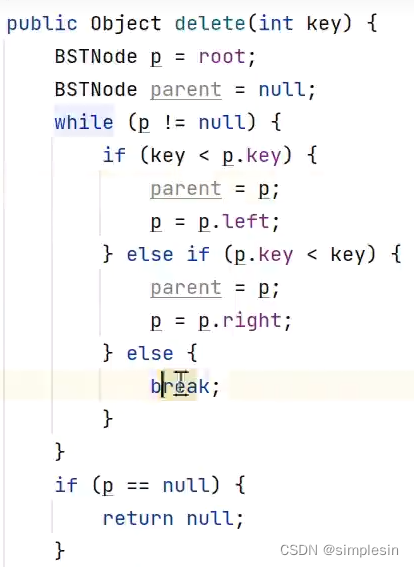

126 二叉搜索树 删除3

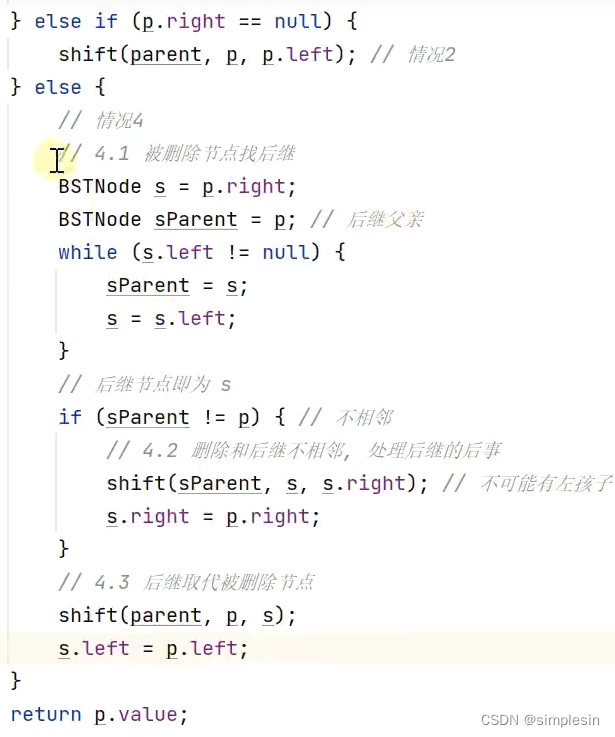
127 二叉搜索树 删除 递归1
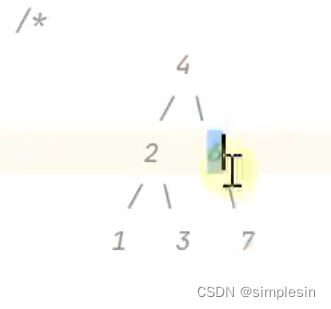
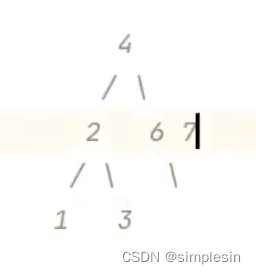
意思是:假如我要删除的是6,那我现在就要将7返回,然后让4指向7,这样就断开了4和6的连接,那就可以删除6了。
因此,通俗来说,就是将要删除的节点的孩子返回,然后让删除节点的父母指向要删除的节点的孩子。
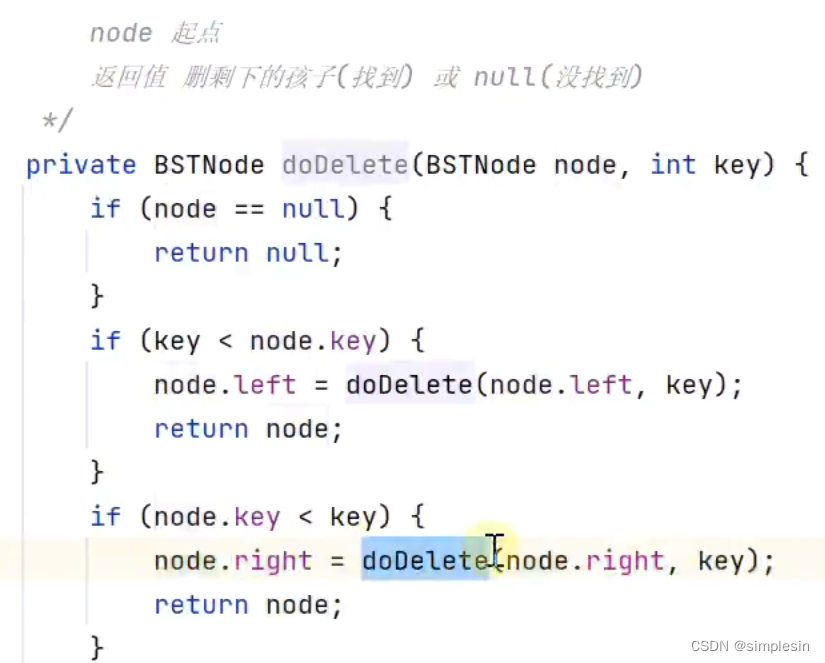
这一部分的代码是找出要删除的节点。因为如果node.key=key就走到后面的代码去了,就不会在着三个if走。

这一部分的代码意思是,拿原先给的图片来做例子
来一个伪递归
private BSTNode doDelete(BSTNode node,int key){
//比如我要删除的是6 key=6
if(node == null){
return null;
}
if(key < node.key){
node.left = doDelete(node.left,key);
return node;
}
if(key> node.key){ 6>4
node.right = private BSTNode doDelete(BSTNode node,int key){//现在传进来的是4的右孩子也就是6,而且6没有左孩子,因此,直接走下面这几行代码
if(node.left == null){
return node.right; //这里的意思是返回6的右孩子,也就是7
} /return node;
}
if(node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
}下一步
private BSTNode doDelete(BSTNode node,int key){
//比如我要删除的是6 key=6
if(node == null){
return null;
}
if(key < node.key){
node.left = doDelete(node.left,key);
return node;
}
if(key> node.key){ 6>4
node.right = private BSTNode doDelete(BSTNode node,int key){//现在传进来的是4的右孩子也就是6,而且6没有左孩子,因此,直接走下面这几行代码
if(node.left == null){
return 7/return node;
}
if(node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
}下一步
private BSTNode doDelete(BSTNode node,int key){
//比如我要删除的是6 key=6
if(node == null){
return null;
}
if(key < node.key){
node.left = doDelete(node.left,key);
return node;
}
if(key> node.key){ 6>4
node.right =7/return node;
}
if(node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
}下一步
private BSTNode doDelete(BSTNode node,int key){
//比如我要删除的是6 key=6
if(node == null){
return null;
}
if(key < node.key){
node.left = doDelete(node.left,key);
return node;
}
if(key> node.key){
node.right =7
return node;//返回6 这个删除的节点
}
if(node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
}而这个时候。因为node.right =7了,因此,树已经连接好,就是被删除节点的父母已经找到了要删除节点的孩子,也意味着6已经被删除了,因为已经没有人和它牵手了。
![]()
这里的作用是:连接被删除节点的孩子们和被删除节点的父母的关系
128 二叉搜索树 删除 递归2

node是指要删除的节点
node 是4,node.right 是5,因此s是5,进入循环,找到node的右孩子的左孩子
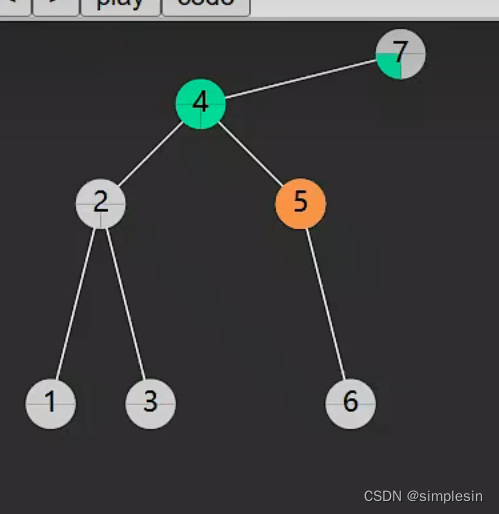
让原来node(被删除节点的左孩子全部托付给s,也就是托付给5)
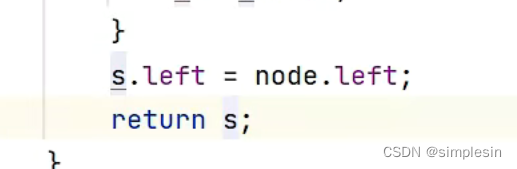

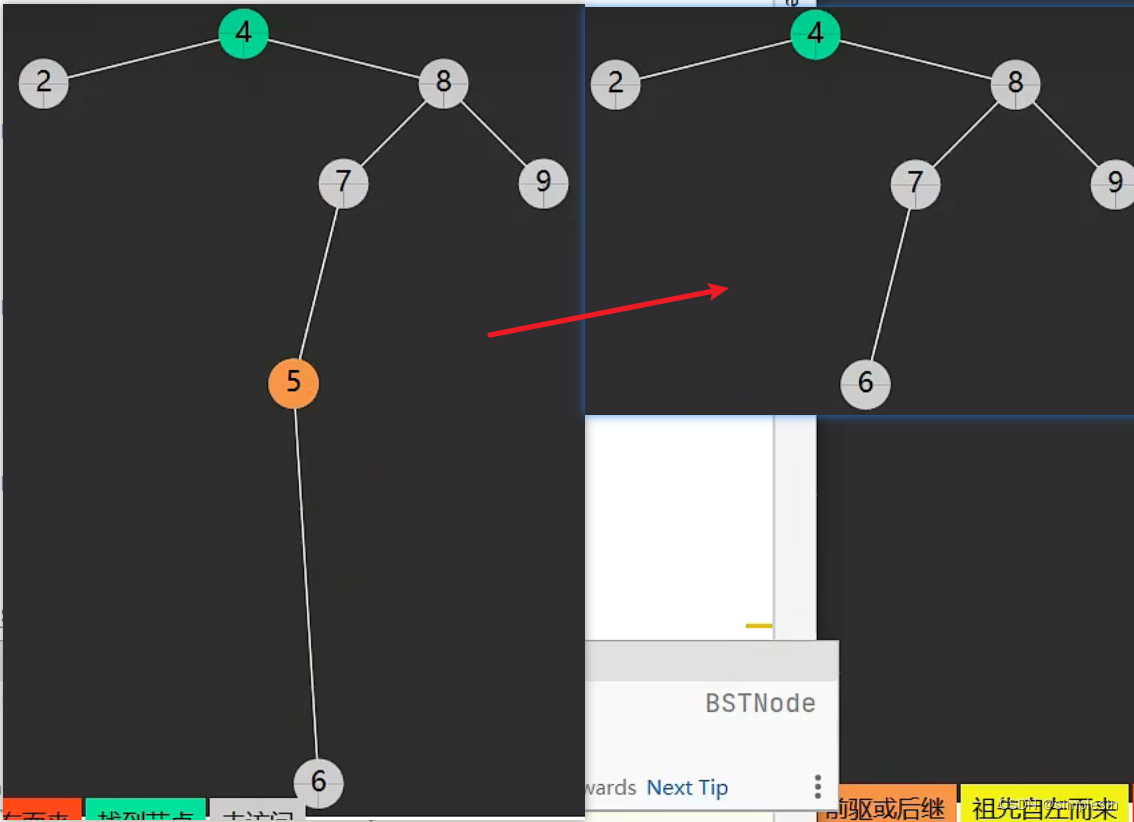
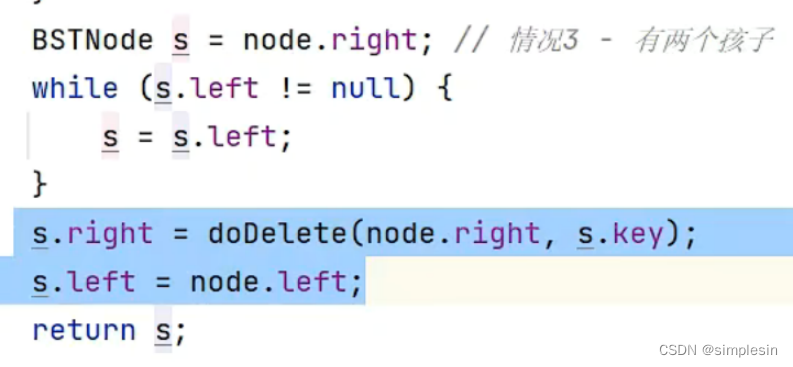
可是如果要删除的节点和根节点之间有距离,需要再加一些步骤。
那这个时候就有疑问了,那会不会和没有距离的那些情况搞混淆了?不会的,他这里就是加了一步递归,实际上就是做了一次无用功。还是拿刚才的例子做说明。
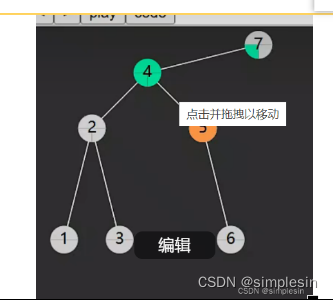
node 是4 s是5
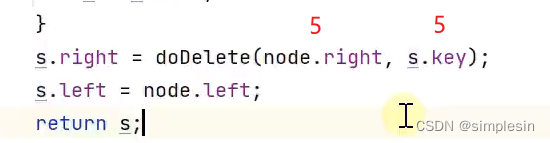
我这里传进去的都是5,而且5只有右孩子,因此,doDelete这个方法中它直接走下面这行代码 。return的就是6

所以,s.right 还是等于6,因此没有改变任何东西,只是做了无用功。
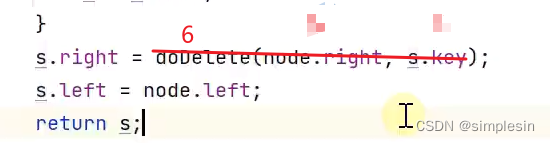
回归正题,如果就是根节点和被删除节点之间就是隔了很多的元素,那代码解读应该如下 :
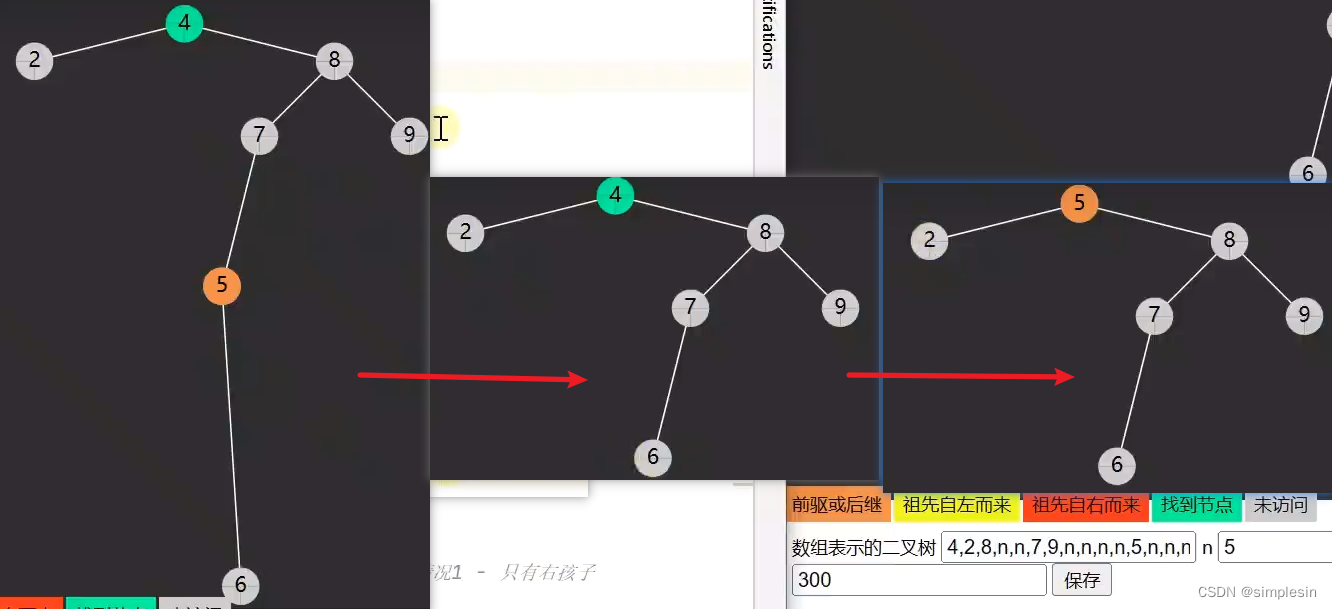
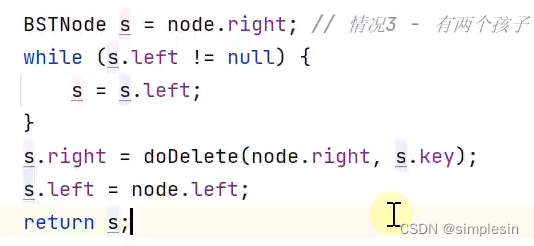
先解释一下图片的含义:4是被删节点,5是要后继节点。首先先将5拿开,让6和7进行相连接,然后再删除4,让5替代4的位置。因为如果倒数第二行和倒数第三行的代码调换过来的话,就会导致图片1的5那里有两个孩子,增加麻烦。
好的,我们来解释一下代码:
将4的右节点也就是8和4的后继节点也就是5传入doDelete,也就是将以8为树根的这棵树传进去,删掉5,之前的伪代码演示中可以发现doDelete可以删除5操作。因此就从图一转换为图二
node.left是2,将这个2这个孩子交给s,成为s也就是5的做左孩子。
129 二叉搜索树 范围查询
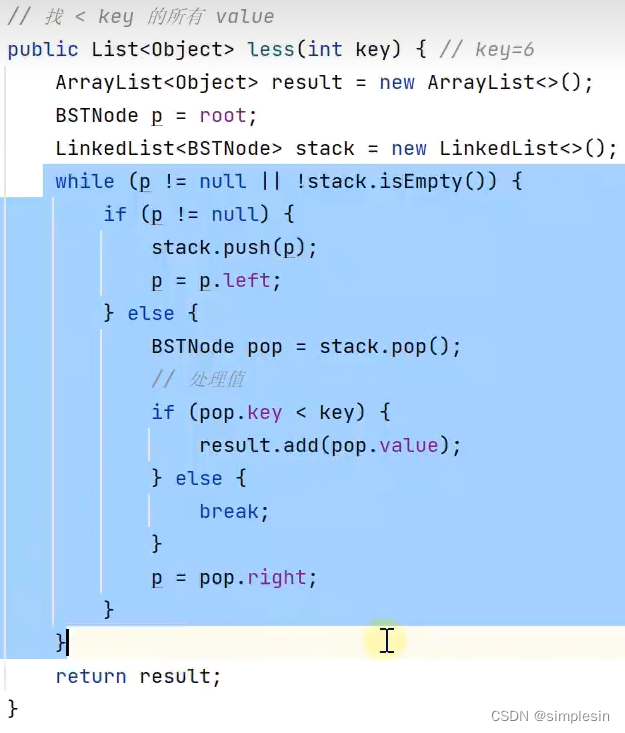
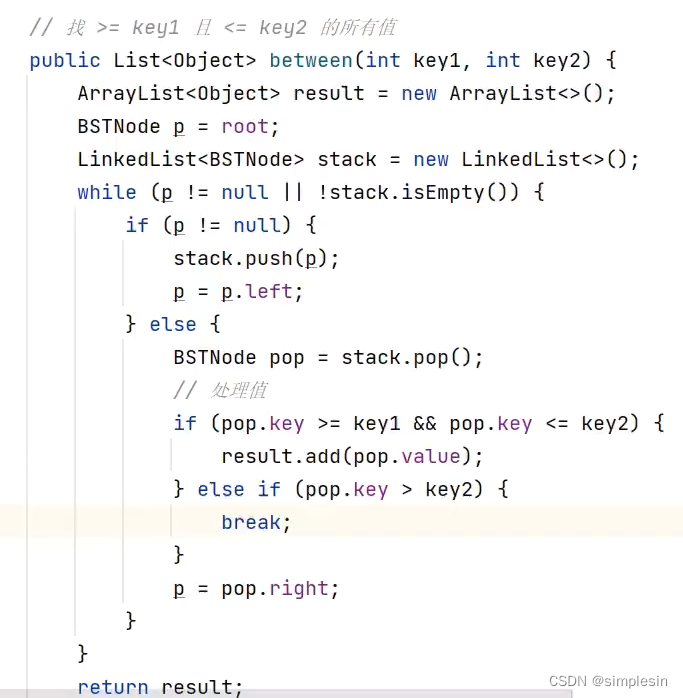
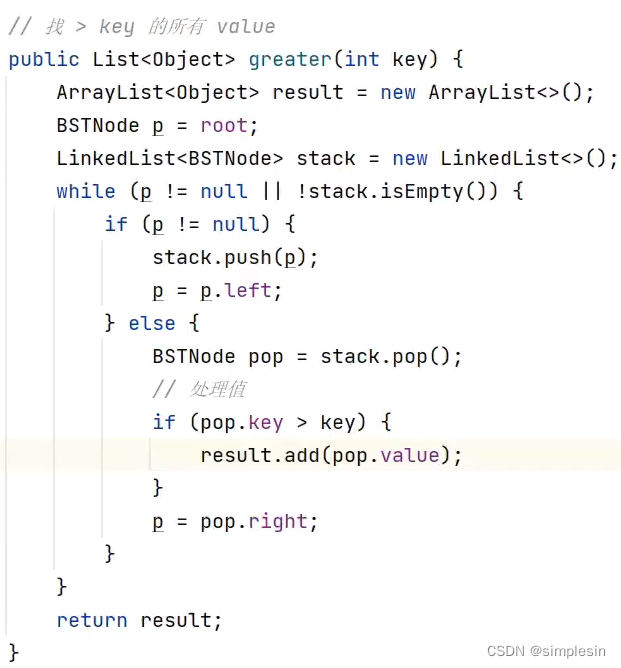

但是,对于greater方法来说,如果用正着来遍历的话,就得把所有都遍历完,但如果采用反向遍历,就不需要。因此,优化代码:
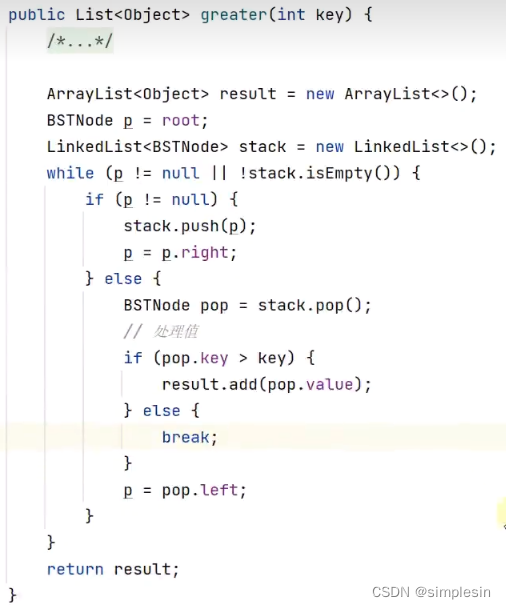
最终完整的代码:
因为最后的最后返回的是被删除节点,因此,要创建一个集合来收集被删除元素,而被删除元素又只有一个,因此,取【0】即可以。
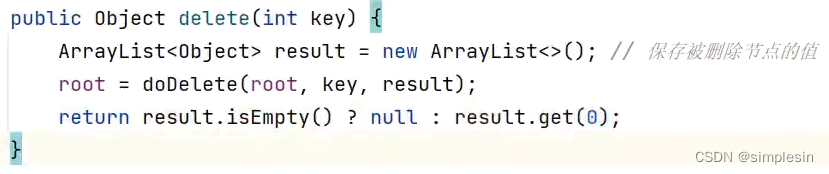
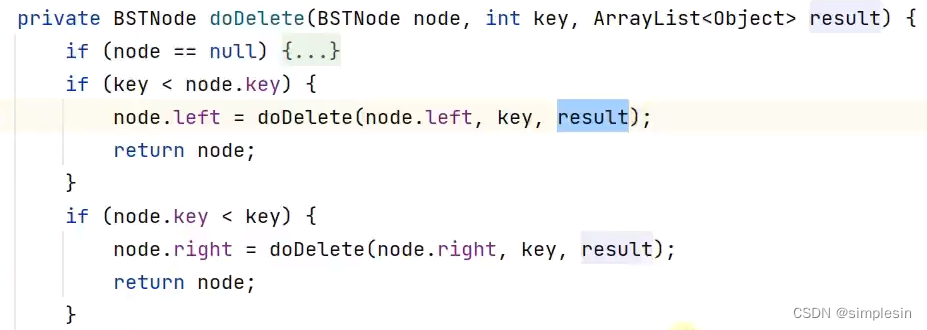
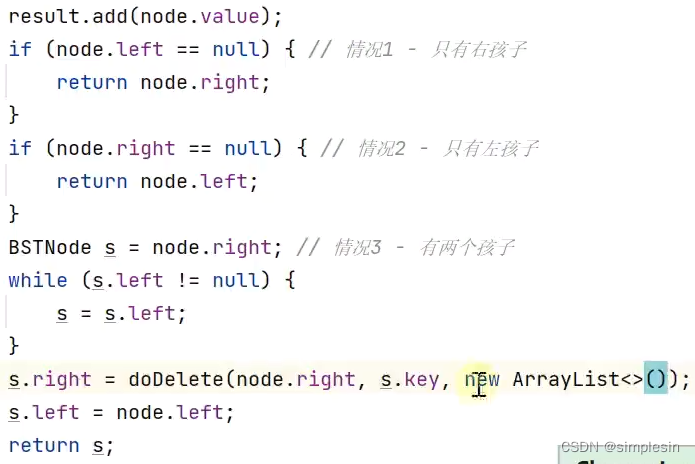
130 二叉搜索树 e01-e03 删增查

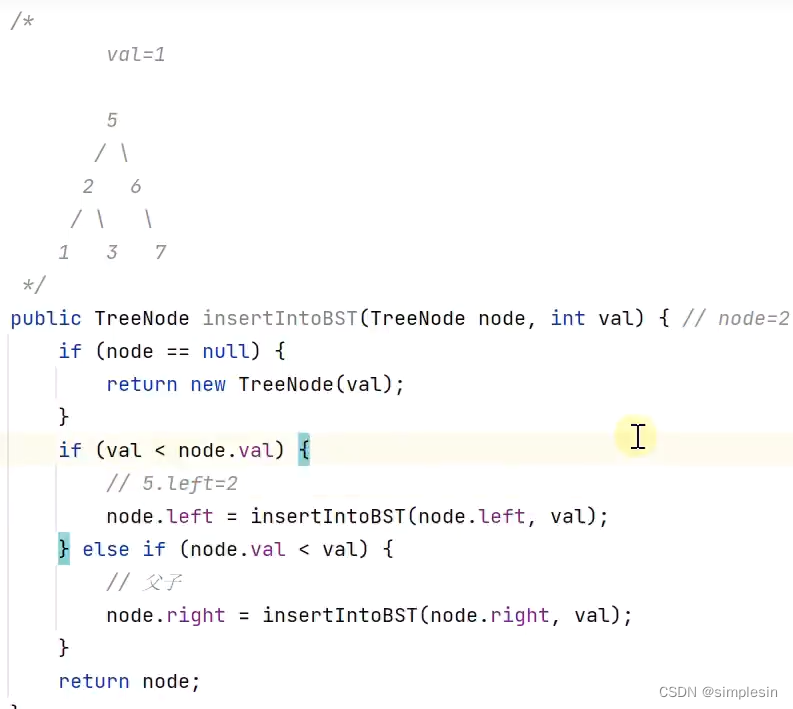
递归有一些缺点就是,做了一些不必要的操作,比如我要新增1,但是在递归的过程中,又把已经连接好的5和2又连接一次。
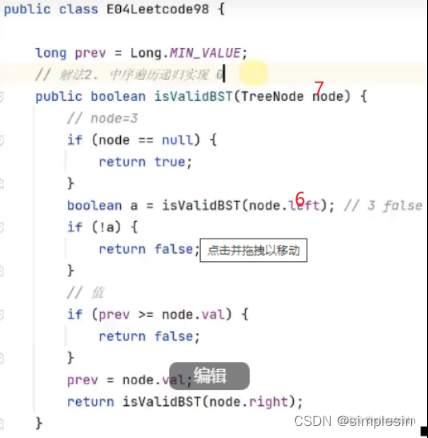
131 二叉搜索树 e04 判断合法 中序非递归
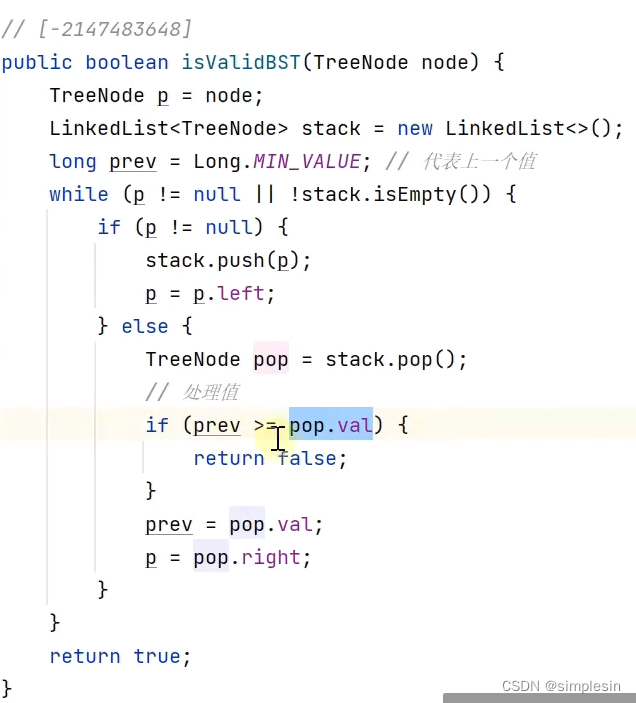
Long的最小值小于整数的最小值。
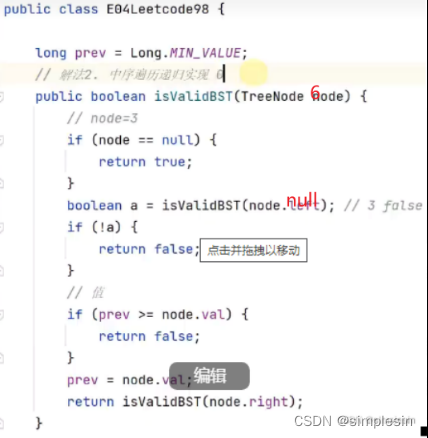
132 二叉搜索树 e04 判断合法 中序递归1

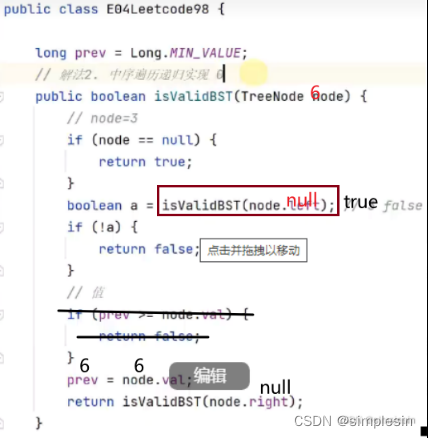
进行优化,以下:
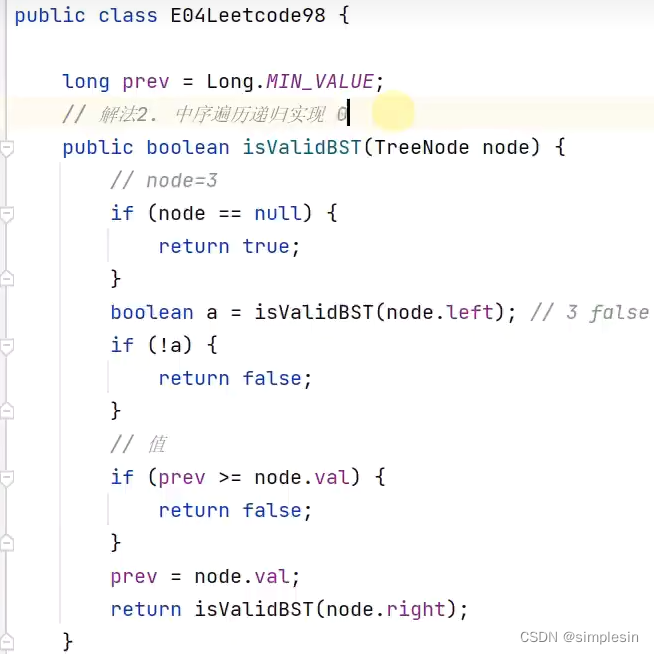
解释一下为什么是在boolean a 下面添加if判断:因为isValidBST (node.left )传进去的是6的left,也就是传进去的3,因此,a的真假是说明3是否符合条件。那既然3不符合的话,直接返回false就好了,就没有必要还去比较6这个值了。 这种行为也叫做剪枝。

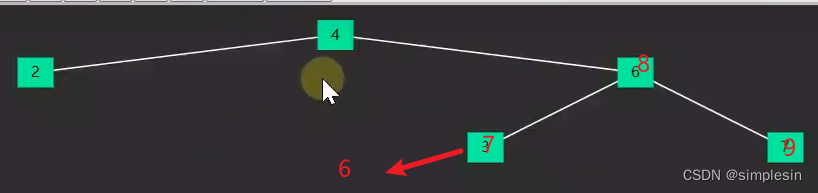
如果是这样,该怎么遍历呢?直接从8开始。
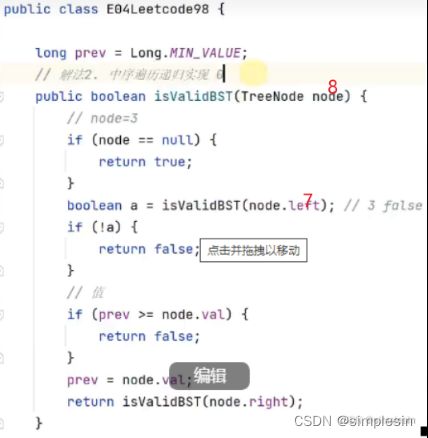
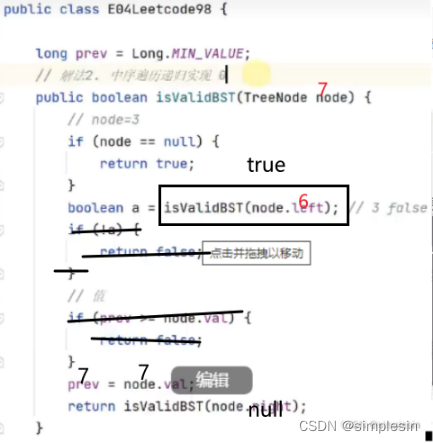
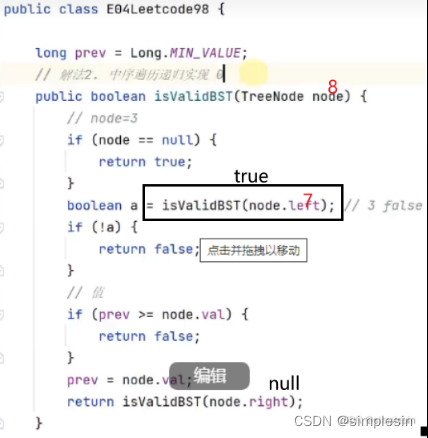
红色的是来,黑色(深紫色也算黑色,当时搞错颜色了而已)的是回。
一层层走。
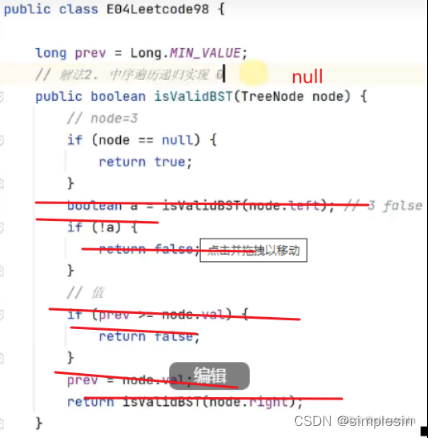
133 二叉搜索树 e04 判断合法 中序递归2
局部变量在一个方法中发生了改变,不会影响其他的方法。因此要把它放到全局去看
第一种修改方式:

第二种修改方式:
创建一个对象,而不是一个变量。Long和Integer都不行,它们的值不可以发生改变,一定要AtomicLong,因为它可以改变。
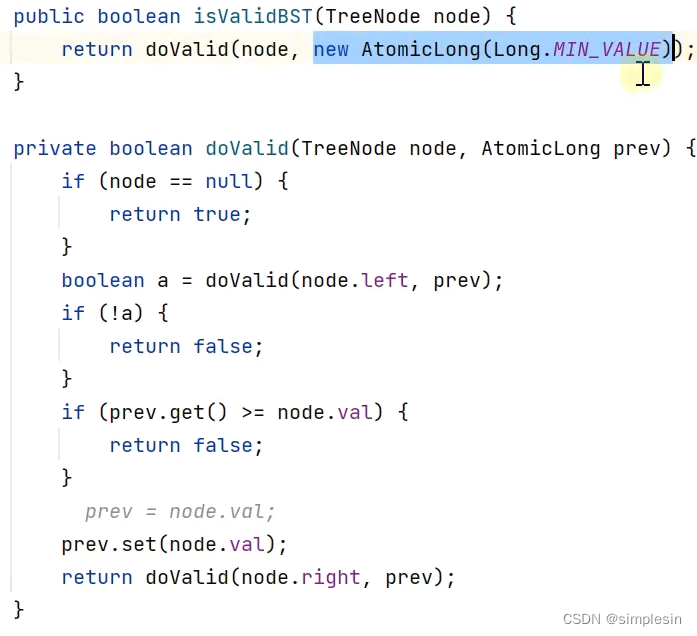
一些小方法:
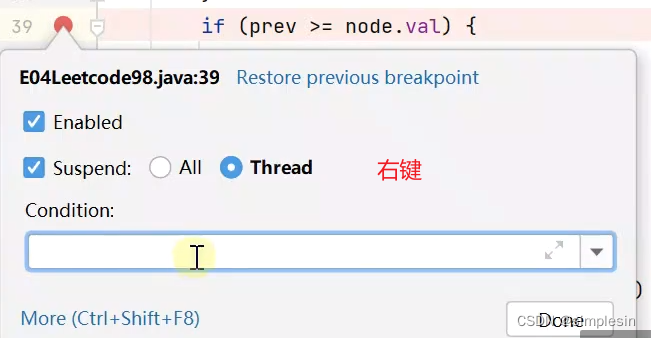
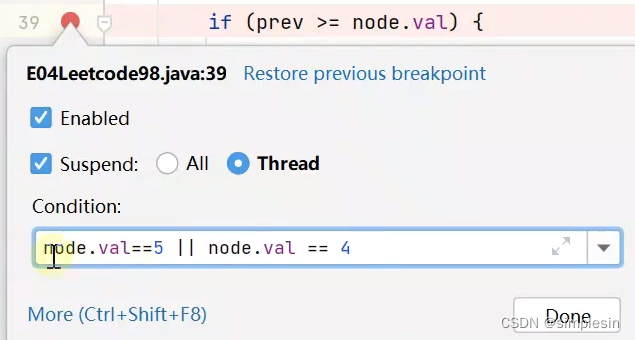
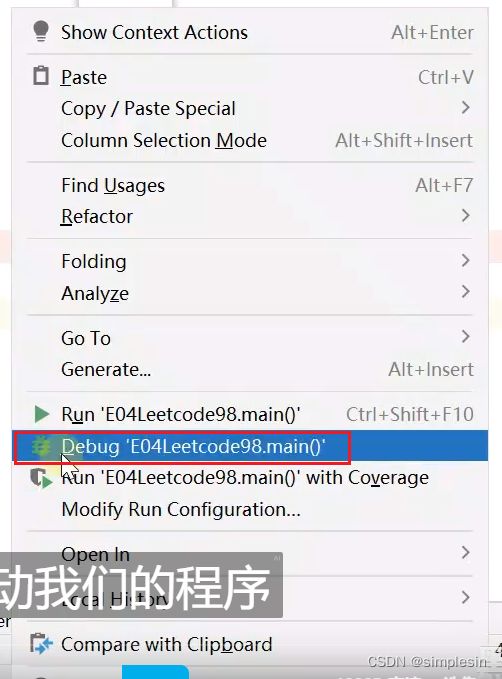
134 二叉搜索树 e04 判断合法 上下界


135 二叉搜索树 e05 求范围和
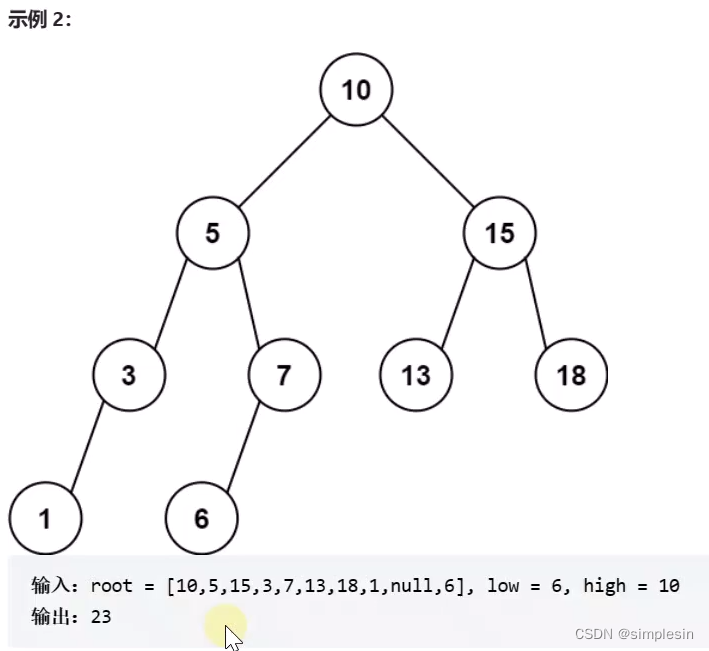
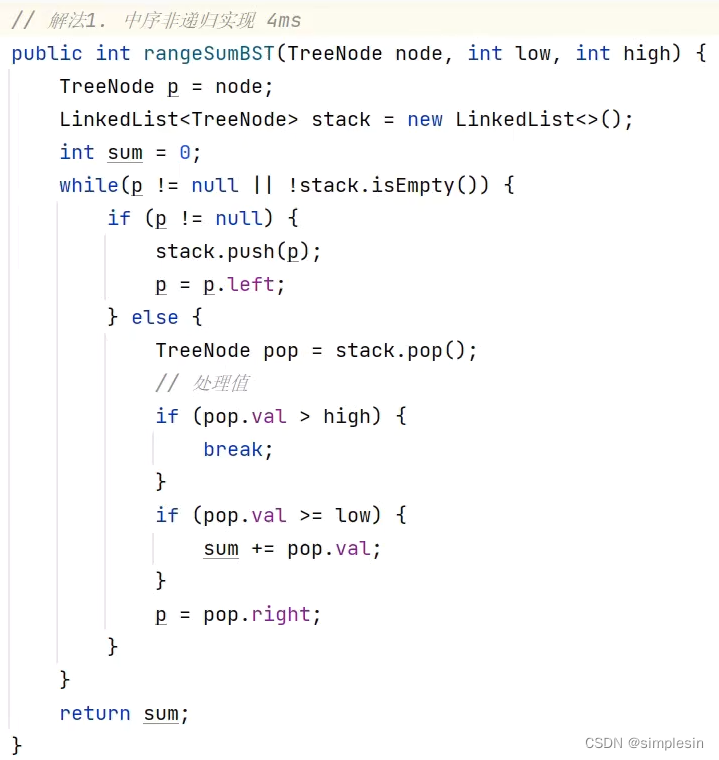
第二种方法:伪递归来一次

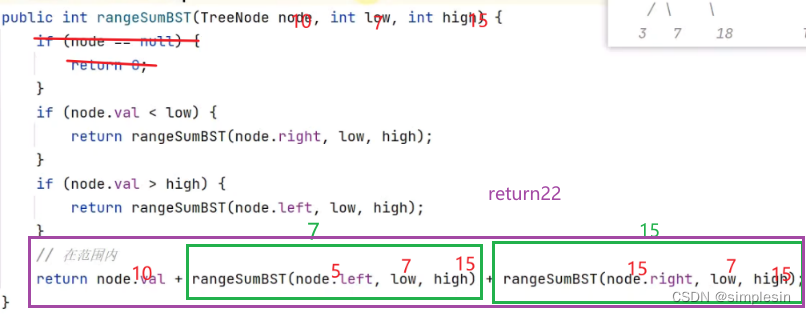
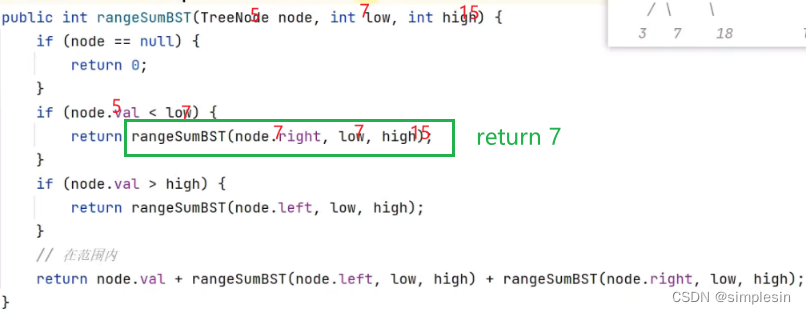



红色的是来,绿色的是回,紫色的是最后一步
136 二叉搜索树 e06 根据前序遍历结果建树1
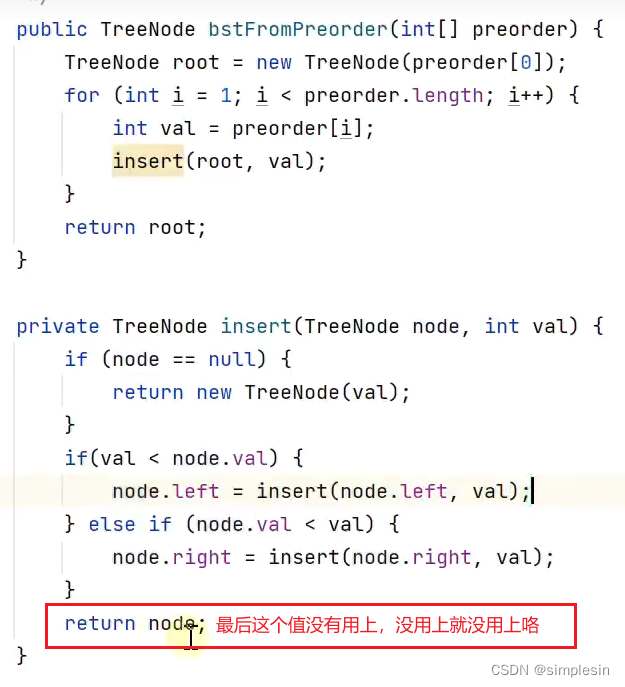
137 二叉搜索树 e06 根据前序遍历结果建树2



理解:
先拿个8过来,确立好的左限和右限,然后拿5。5小于8,可以做为8的左孩子。然后拿1,1小于5,可以做5的左孩子。然后拿7, 7大于5,因此,1的左右孩子为null,完毕。然后拿10。10超过了5的上限,因此5完毕。。以此类推。。

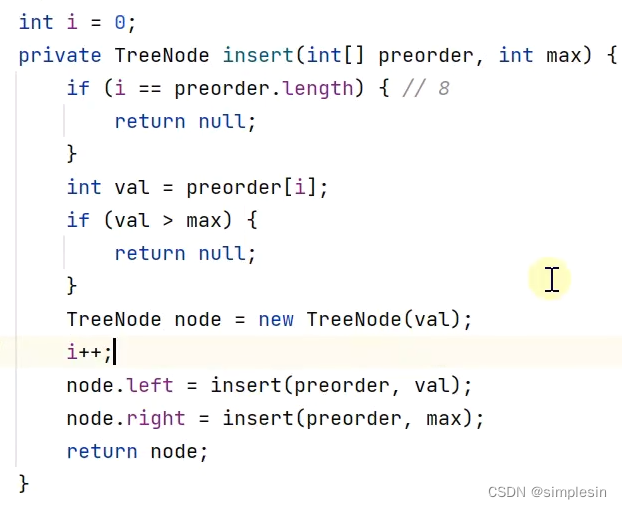
138 二叉搜索树 e06 根据前序遍历结果建树3

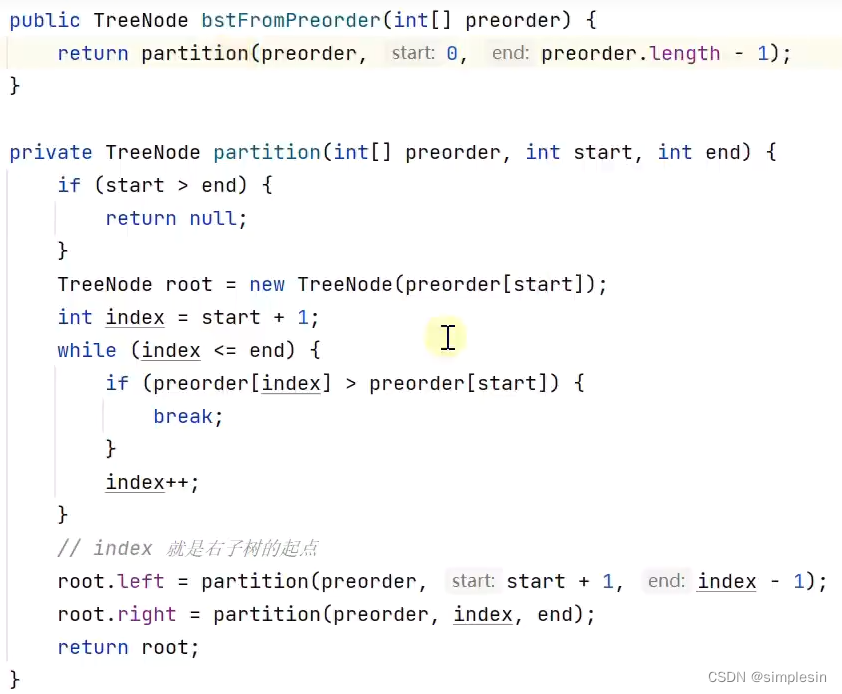
139 二叉搜索树 e07 最近公共祖先


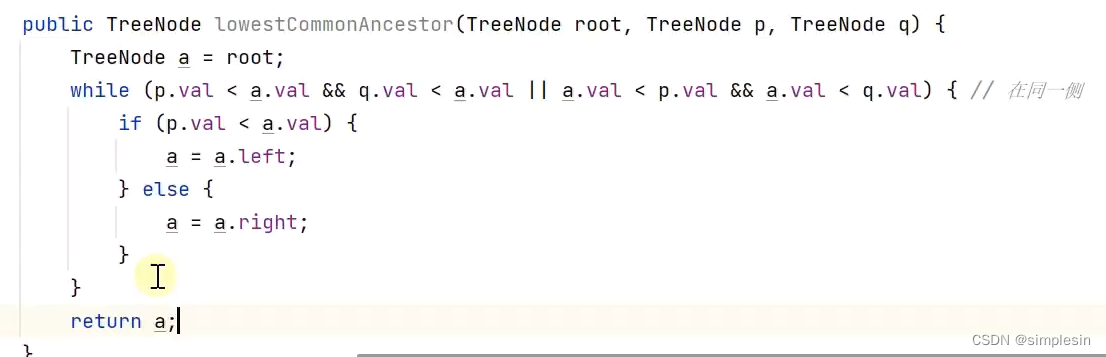
140 avl树 概述
![]()
导致失衡的原因:删除,添加。

141 avl树 高度和平衡因子
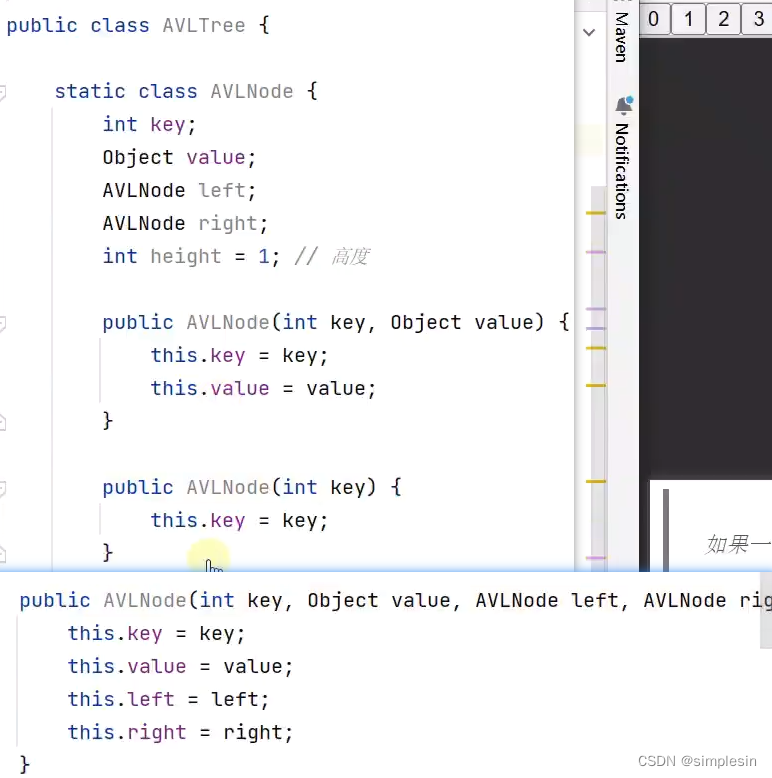
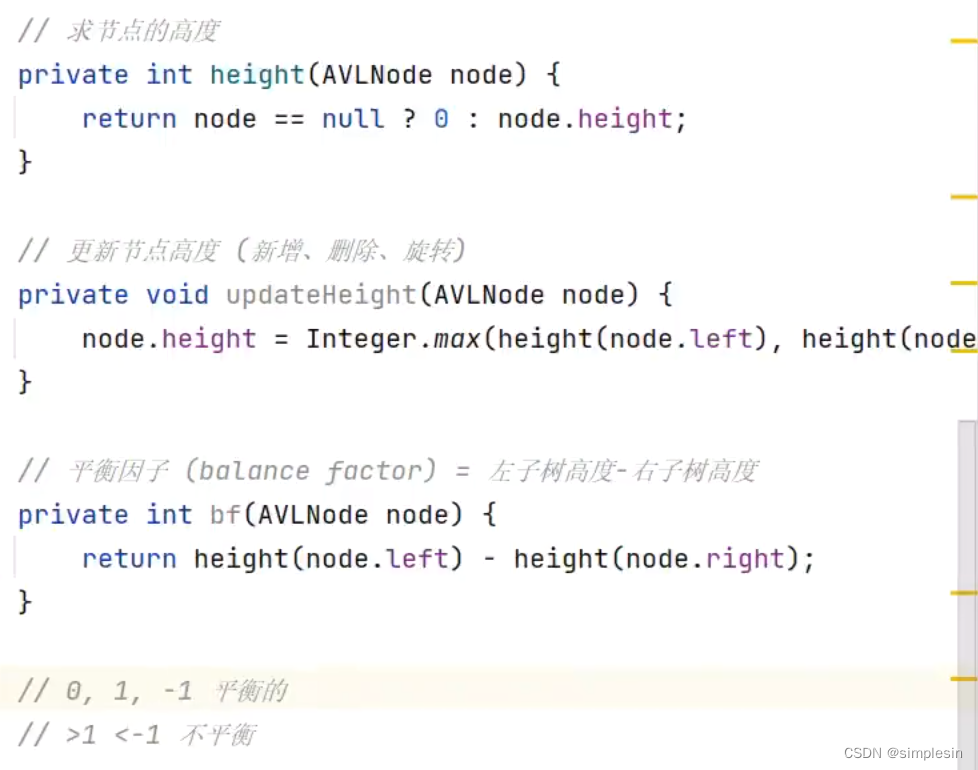

142 avl 四种失衡情况
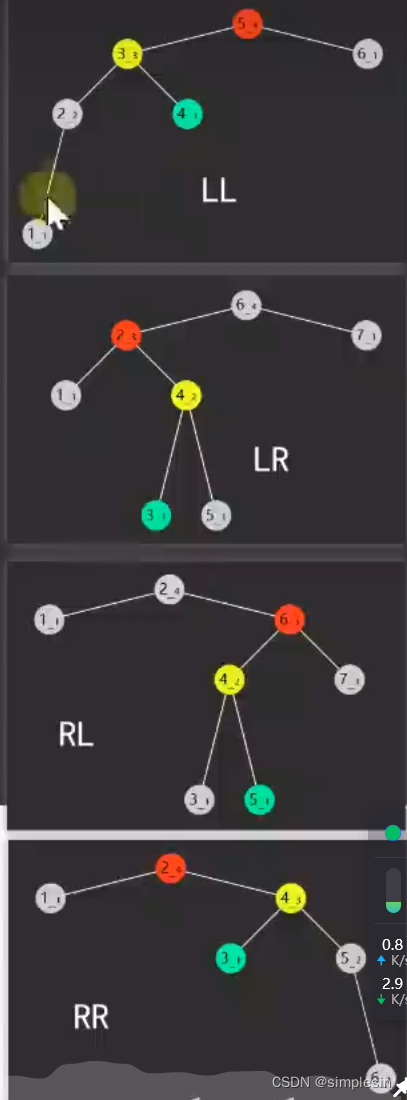

对于LL和RR只要做一次旋转:
LL:失衡点向右旋转一次
RR:失衡点向左旋转一次
对于LR和RL要做两次旋转:
LR:先让失衡点的右孩子左旋转,再让失衡点右旋转
RL:先让失衡点的左孩子右旋转,再让失衡点左旋转
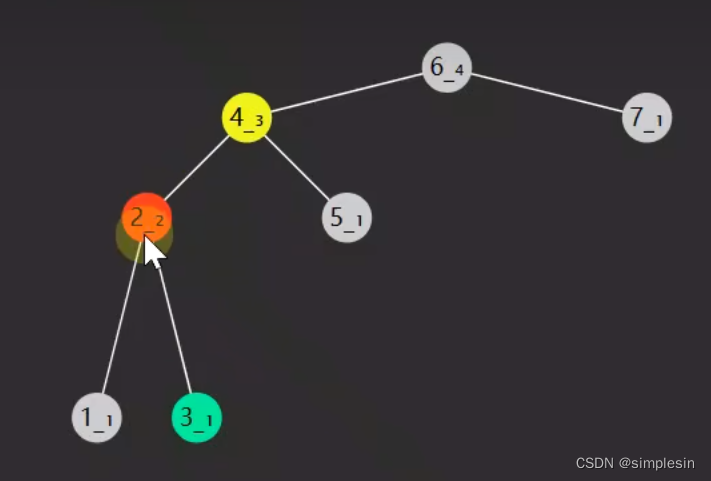
143 avl 旋转
要先更新红色节点才能更新黄色节点,要先将下面的高度算好,才可以算上面的高度,这样才会准确。




这篇关于12.14_黑马数据结构与算法笔记Java的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





