本文主要是介绍数组两端取数问题中的先手优势,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数组两端取数问题中的先手优势
一:问题背景
今天给大家分享一个LeetCode的算法题,其实不是出自于leetcode,出自我们ChallengeHub公众号同学的面试题目。
二:问题描述
已知任意一个正整数的数组nums,它满足两个条件:
a、元素的个数是偶数,b、所有数据的和为奇数
现在指定A,B两个人轮流从这个数组中取数,但是每个人只能从首或尾选择1个。两人依次拿完之后,各自将其手上所有的数字加起来,谁的和大谁取得胜利。
例子:
[5,3,4,5]
A先选择5,B也选择5,A再选择4,B再选择3。
最后A的总和是9,B的总和是8,因此A获得胜利
现在假设A,B都是理性人,以取得胜利为目标,请问这种游戏有没有先手优势,如果有的话,那么给定一个符合要求的数组,A手上的数总和最大可以领先B多少?
Input: [5,3,4,5]
out: 1
inpit [6,100,20,9]
out:83
这个问题是群内某个人在富途的面试中遇到的,个人感觉难度较大,问题描述简单,大家面试的时候很可能会遇到,于是分享给大家。该题由群内的ACM选手雪研完成(膜拜大佬)。代码如下:

如果基础很好的,或者喜欢磕代码的那么直接看代码就好了,如果发现难以理解的话,下面我会针对该代码进行讲解。
三:问题分析
当每个人取完一个数字之后,剩余的数组还是偶数的,如果我们可以把AB在剩余数组中取数的最优解求解出来,那么加上之前选取的2个数字之差,就是我们需要求得的最优解。于是,很容易想到可以采用动态规划的方法来倒推,用一个状态变量来表示剩余数组的最优解。因此我们可以采用如下的方法定义状态变量。
状态变量:
dp[i][j]:表示的是将子数组nums[i:j+1]交给AB两人选择最后的结果。
由于AB两人选择的结果一定是偶数,因此j+1-i也是偶数。dp[0][n-1]就是我们需要求的最终结果,n代表数组的长度。
比如数组[4,7,2,9,5,2],假如数组只有从[2,9]这一小段的话话,那我们的最终结果很容易得出来,dp[2][3]=7。同理dp[1][2]=5,dp[3][4]=4。
状态转移方程:
当j-i等于1的时候,那么dp[i][j]就自动等于abs(nums[i]-nums[j])了。如果j-i等于3时,有以下四种方法可以达到这种状态:
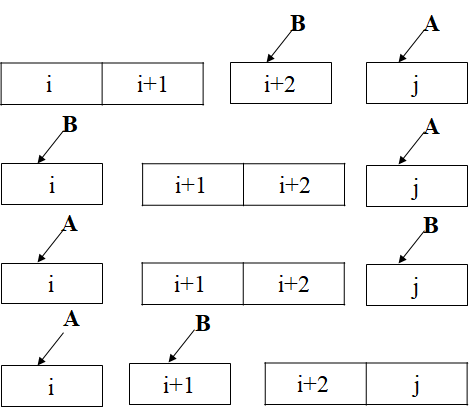
从上面可以看到,为了达到dp[i][j]这个状态,A有2种选择,针对A的每种选择B也有2种选择。
假如A选择了i,那么B势必要从可以达到状态dp[i][j]的两种方法种选择对自己更有利的方法:
1min(dp[i+1][i+2]+nums[i]-nums[j],
2 dp[i+2][j]+nums[i]-nums[i+1])当A选择的是j是那么同样B还是会选择对自己最有利的方法:
1min(dp[i][i+1]+nums[j]-nums[i+2],
2 dp[i+1][i+2]+nums[j]-nums[i])
当然A也知道B可能应对的方法,因此他也会选择对于自己最有利的方法,于是:
1dp[i][j]=max(
2 min(dp[i+1][i+2]+nums[i]-nums[j],
3 dp[i+2][j]+nums[i]-nums[i+1]),
4 min(dp[i][i+1]+nums[j]-nums[i+2],
5 dp[i+1][i+2]+nums[j]-nums[i])
6)
同理,去除j-i等于3这个条件,对于任意j-i-3=2k(k>=1)来说,状态转移方程为:
1dp[i][j]=max(
2 min(dp[i+1][j-1]+nums[i]-nums[j],
3 dp[i+2][j]+nums[i]-nums[i+1]),
4 min(dp[i][j-2]+nums[j]-nums[j-1],
5 dp[i+1][i+2]+nums[j]-nums[i])
6)
四:代码解读
关于状态变量和转移方程的讲解,就到此结束的,现在让我们来欣赏下大佬的代码:
1nums=[4,7,2,9,5,2]
2n=len(nums)
3dp=[[0 for col in range(n)] for raw in range(n)]
首先定义dp状态变量。
1if n%2==1:
2 for i in range(n):
3 dp[i][i]=nums[i]
4 lens=2
5else:
6 for i in range(n-1):
7 dp[i][i+1]=max(nums[i],nums[i+1])-min(nums[i]-nums[i+1])
8 lens=3
第二步,初始话状态变量,代码这里写多了,考虑了nums数组为奇数的情况。
1while lens<n:
2 for i in range(n-lens):
3 dp[i][i+lens]=max(min(nums[i]-nums[i+1]+dp[i+2][i+lens],
4 nums[i]-nums[i+lens]+dp[i+1][i+lens-1]),
5 min(nums[i+lens]-nums[i+lens-1]+dp[i][i+lens-2],
6 nums[i+lens]-nums[i]+dp[i+1][i+lens-1]))
7 lens+=2
第三步,更新状态变量,当n等于lens-1时,dp[0][lens-1]就是我们需要求的结果了。
以上就是该题目的所有的解答了,个人认为是一个比较好的题目,涉及到博弈论的动态规划问题,求解的时间空间复杂度均为O(n^2)。
五:问题拓展
群里的大佬看了这题之后,想到了另外一题,是ACM的某个题目,与此题有些类似。具体的问题描述如下所示:
同样是一个数组,长度不限,数组内可能存在负数,AB轮流取数,一个玩家只能从左边或者右边取,可以取任意数量的数(数量大于等于1),不能边都取,当所有的数被取完后即停止。统计各自手上数的和作为各自的得分,两个都是理性人,期望自己的分数尽可能地高,求最后AB得分之差。
input:[4,-10,-20,7]
out:7
解释:A先选取了4,然后B选取了7,A然后选取了-10,B选取了-20。
input: [1 2 3 4]
out:10
解释:A将1234全部取走了
问题分析:由于AB会将所有的数字全部取走,并且A是理性人,那么A选择完之后,为了防止B得分高,需要尽可能地让B的得分变得低。
假设dp[1][n]为A先手的得分,那么sum(nums)-dp[1][n]就是B的得分。A要想得到更高的分,那么B的得分就需要变低,因此我们可以得到:
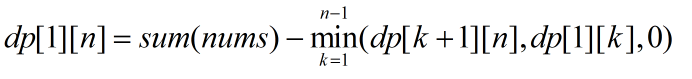
假设k=t时,dp[1][t]取得最小值,那么如果A把t+1到n的数字全部取了,那么等到B取的时候只剩下了1到t的,如此的话B就只能获得最小的值,反过来的话A就相当于获得了最大的值。如果dp[k+1][n],dp[1][k]都大于0的话,那么A就可以取走所有的数字。
通过上述的方程我们可以推广转移方程:
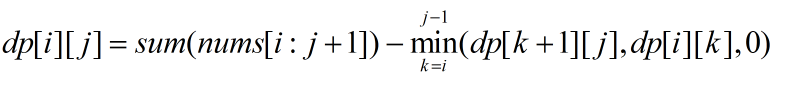
无论给A一串什么数组,只要留给B的保证B先手取得的结果是最小的就OK啦。
代码如下:
1nums=[-1,-2,-3,-4,-5,-6,-7,-8]2lens=len(nums)3vis=[[0 for _ in range(lens)] for _ in range(lens)]4dp=[[0 for _ in range(lens)] for _ in range(lens)]5sum=[0]*lens6for i in range(lens):7 sum[i]=sum[i-1]+nums[i]8def dfs(i,j):9 if vis[i][j]:
10 return dp[i][j]
11 vis[i][j]=1
12 m=0
13 for k in range(i,j):
14 m=min(m,dfs(i,k))
15 for k in range(i,j):
16 m=min(m,dfs(k+1,j))
17 if i==0:
18 dp[i][j]=sum[j]-m
19 else:
20 dp[i][j]=sum[j]-sum[i-1]-m
21 return dp[i][j]
22print(2*dfs(0,lens-1)-sum[-1])
六:尾言
关于两端取数的先手优势就到此结束,想了解更多算法,数据分析,数据挖掘等方面的知识,欢迎关注ChallengeHub公众号,添加微信进入微信交流群,或者进入QQ交流群。


这篇关于数组两端取数问题中的先手优势的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







