数据结构第六课 -----排序

2023-12-12 20:36
文章标签 数据结构 排序 第六课

本文主要是介绍数据结构第六课 -----排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

作者前言

🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂
​🎂 作者介绍： 🎂🎂
🎂 🎉🎉🎉🎉🎉🎉🎉 🎂
🎂作者id：老秦包你会， 🎂
简单介绍：🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂
喜欢学习C语言和python等编程语言，是一位爱分享的博主，有兴趣的小可爱可以来互讨 🎂🎂🎂🎂🎂🎂🎂🎂
🎂个人主页::小小页面🎂
🎂gitee页面:秦大大🎂
🎂🎂🎂🎂🎂🎂🎂🎂
🎂 一个爱分享的小博主 欢迎小可爱们前来借鉴🎂

排序

  • **作者前言**
  • 直接插入排序
  • 冒泡排序
  • 希尔排序
  • 直接选择排序
  • 堆排序
  • 快速排序
      • hoare版本
    • 优化点
      • 三数取中
    • 小区间优化
    • 挖坑法
    • 前后指针版本
  • 疑惑

直接插入排序

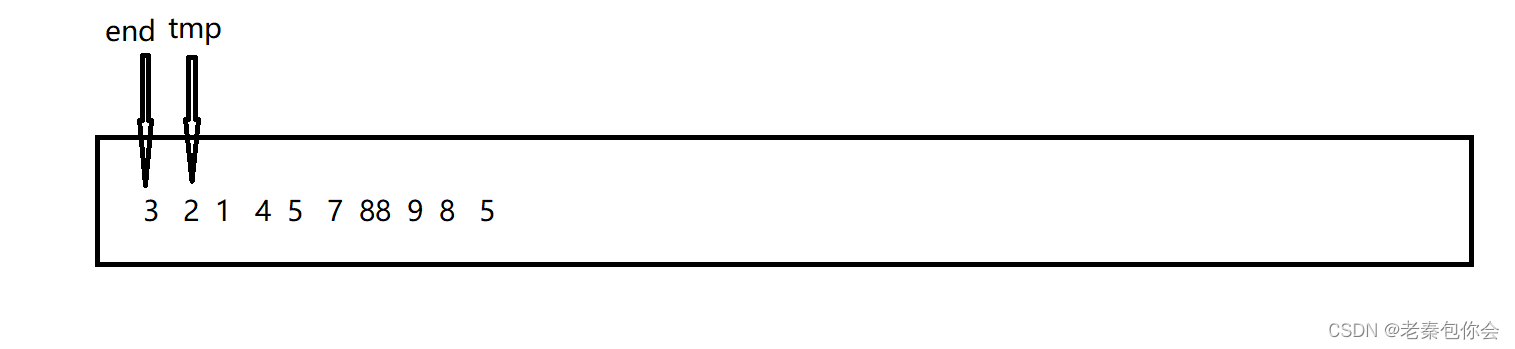
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

思路： 我们要记得[0,end]是有序的,我们要把tmp的值插入到[0,end]就要进行判断,直到tmp等于数组的长度结束,这个过程中我们要注意到我们把tmp插入到[0,end] 是要遍历[0,end]的当我们判断当前的元素大于tmp,就把这个元素往后移动,我们就要往后一个元素比较,直到碰见比tmp小的元素,并再该元素后面插入,如果碰见了在[0,end]都没有小于tmp的元素,我们就要在下标为0的地方插入,

void InsertSort(int* a, int n)
{//[0,end] int i = 0;for (i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){//往后移动a[end + 1] = a[end];end--;}else{break;}}//这个写法一箭双雕,一来可以防止end为-1的情况不用去判断,二来可以插入到a[end + 1]a[end + 1] = tmp;}
}

冒泡排序

在这里插入图片描述

// 冒泡排序
void Bubblisort(int* a, int n)
{int i = 0; for (i = 0; i < n - 1; i++){//如果该数组是一个有序数组,只需遍历一遍下面的就可以了,时间复杂度为O(N)bool excheng = false;int j = 0;for (j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]){int c = a[j];a[j] = a[j + 1];a[j + 1] = c;excheng = true;}}if (excheng == false)break;}
}

时间复杂度是O(N^2), 最好的情况就是O(N)

希尔排序

在这里插入图片描述

分成两步:
1.预排序 (接近有序)
2.直接插入排序
思路:
在这里插入图片描述
相同颜色的框进行插入排序,因为多少种颜色是有gap的数值决定的,每一种颜色对应的是整个数组的一部分

//预排序int gap = 3;int i = 0;//有gap个数组for (i = 0; i < gap; i++){//每个数组进行插入排序int sub = i;while (sub <= n - 1 - gap){int end = sub;int top = a[end + gap];while (end >= 0){if (top < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = top;sub += gap;}}

上面这种是一组组进行插入排序.如果是多组进行插入排序

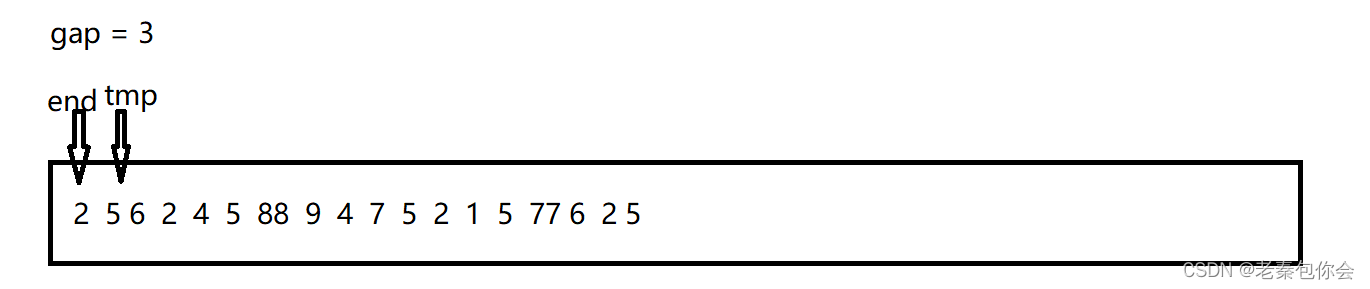
在这里插入图片描述
思路就是我们仍然采用上面的方法,但是我们是多组进行插入排序,仍然是相同颜色的进行插入排序

//预排序int gap = 3;int i = 0;//有gap个数组for (i = 0; i <= n - 1 - gap; i++){//每个数进行插入排序int end = i;int top = a[end + gap];while (end >= 0){if (top < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = top;}

预排序的特点:
gap越大,大的值更快调到后面,小的值可以更快的调到前面,越不接近有序
gap越小,跳得越慢,但是越接近有序,如果gap == 1就是直接插入排序
最终代码为

//希尔排序
void ShellSort(int* a, int n)
{//预排序int gap = 3;int i = 0;//有gap个数组for (i = 0; i <= n - 1 - gap; i++){//每个数进行插入排序int end = i;int top = a[end + gap];while (end >= 0){if (top < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = top;}//直接插入排序InsertSort(a, n);
}

但是我们可以简化一下
我们可以抓住gap=1为直接插入排序

//希尔排序
void ShellSort(int* a, int n)
{//预排序int gap = n;while (gap > 1){//一来gap等于1时,就是直接插入排序,二来就是gap是随n增大的,//再还有就是gap越小,就越接近有序gap = gap / 3 + 1;int i = 0;//有gap个数组for (i = 0; i <= n - 1 - gap; i++){//每个数进行插入排序int end = i;int top = a[end + gap];while (end >= 0){if (top < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = top;}}}

在这里插入图片描述
时间复杂度O（N ^1.3）,这个有点难算,我们只需要理解大概就行

直接选择排序

在这里插入图片描述
思路：从开头开始找，找到最小的，然后进行和开头交换，然后再从剩下的后面继续寻找最小的，依次往后插入
思路图1：这个思路是很多人能想出来的

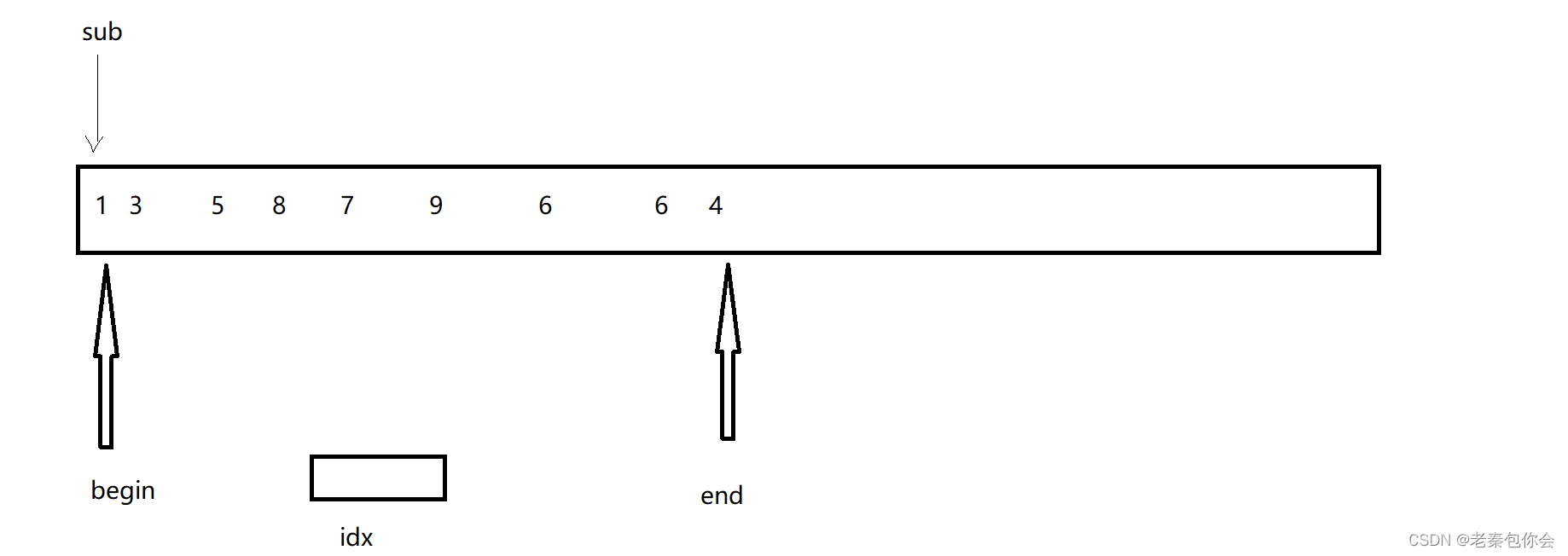
在这里插入图片描述
思路图2：

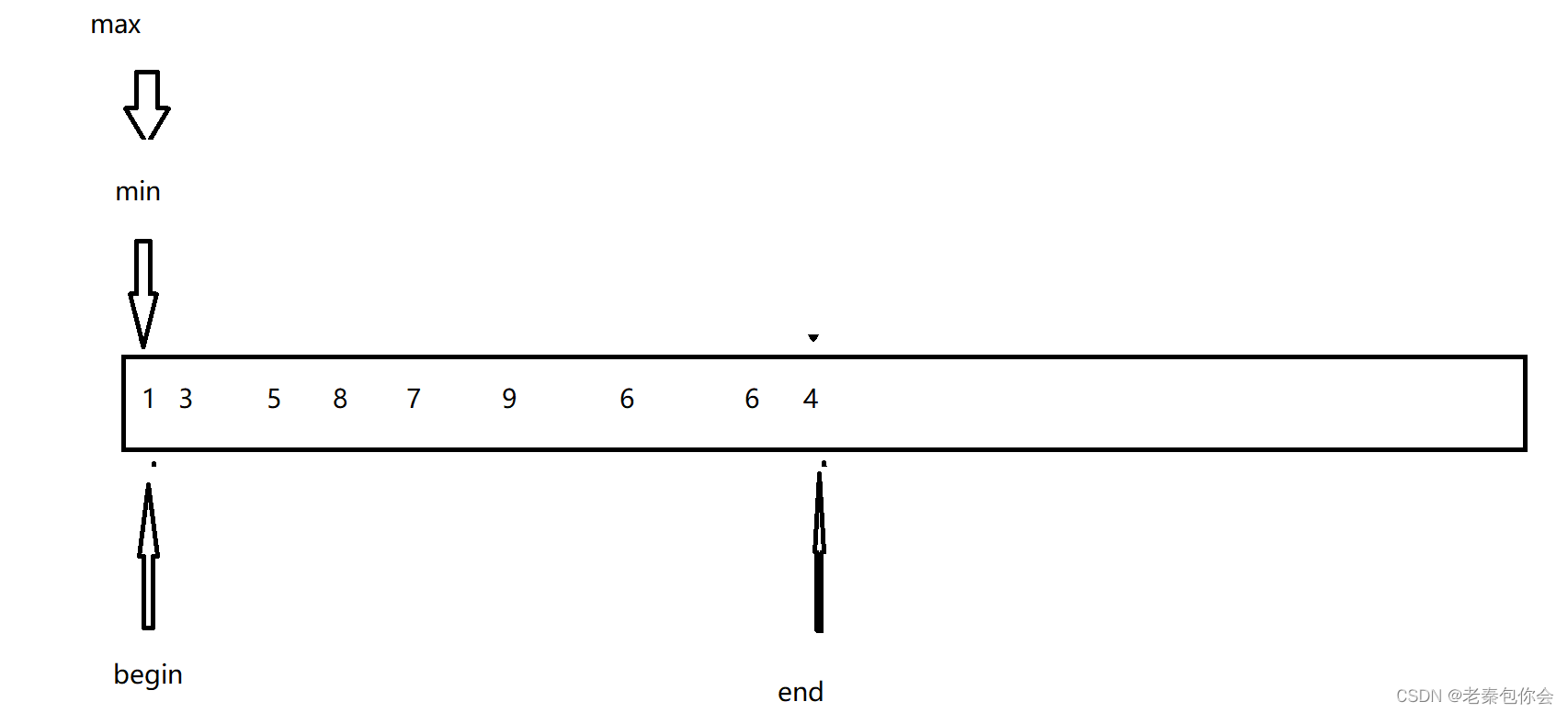
在这里插入图片描述

​这里我是使用了两边，左边插入最小的，右边插入最大的，插入好后，begin往前 ，end往后，直到begin等于end，就停止了

void excheng(int* a, int* b)
{int c = *a;*a = *b;*b = c;
}
//直接选择排序
void SelectSrot(int* a, int n)
{int min = 0, max = 0; //找出最大和最小int begin = 0, end = n - 1;// 在最大和最小的位置插入for (int i = begin + 1; i <= end; i++){int idx = i;while (idx <= end){//找出最小的值if (a[min] > a[idx])min = idx;//找到最大值if (a[max] < a[idx])max = idx;idx++;}excheng(&a[begin], &a[min]);//防止开头就是最大值,一旦最小值交换,就乱了if (max == begin)max = min;excheng(&a[end], &a[max]);begin++;end--;}
}

时间复杂度是 O（N^2）

堆排序

大家可以观看这部博客
堆排序
在这里插入图片描述

//堆排序
typedef int Heapdata;
void exchange(Heapdata* a, Heapdata* b)
{Heapdata e = *a;*a = *b;*b = e;
}
void Heapsort(Heapdata* heap, int size)
{//建大堆int i = 0;for (i = 1; i < size; i++){//向上调整int child = i;int parent = (child - 1) / 2;while (child > 0){if (heap[child] > heap[parent]){//交换exchange(&heap[child], &heap[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}}//开始升序排序while (size > 0){// 根节点和最后一个叶节点交换exchange(&heap[0], &heap[--size]);//向下调整int parent = 0;int child = parent * 2 + 1;while (child < size){if (child + 1 < size && heap[child] < heap[child + 1]){child += 1;}if (heap[child] > heap[parent])exchange(&heap[child], &heap[parent]);elsebreak;parent = child;child = parent * 2 + 1;}}}

快速排序

hoare版本

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止
在这里插入图片描述
这个图可能有点简陋
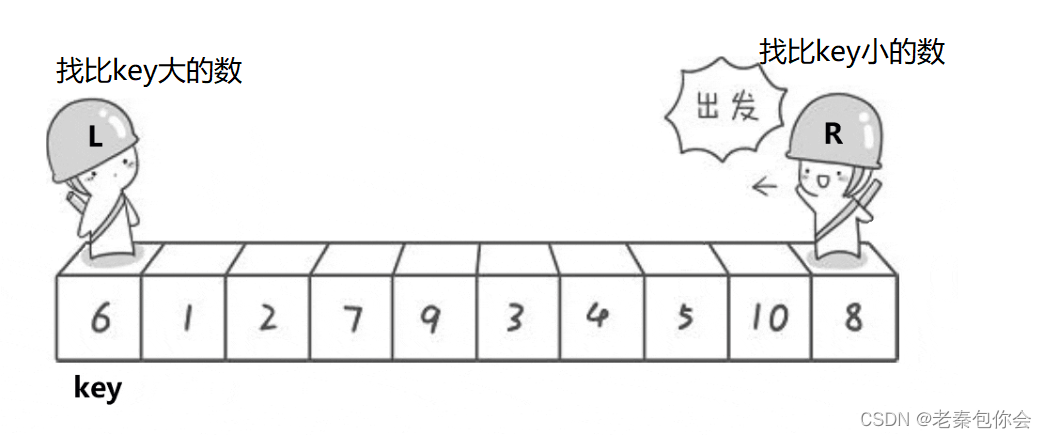
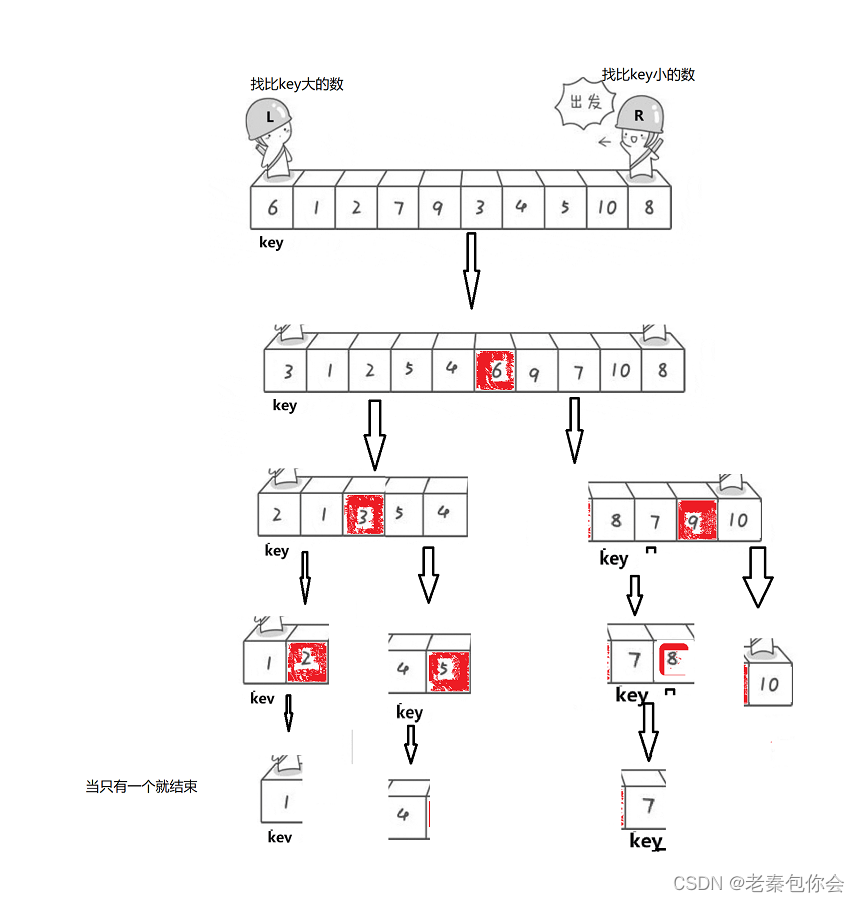
在这里插入图片描述
在这里插入图片描述
时间复杂度：每一次都会把当前数组的每个元素遍历一遍，然后再把key交换， 需要进行log（n）次递归
时间复杂度是：O(n*log(n))
在这里插入图片描述
复杂的话,就如同这个一样,这种情况就是有n层, 时间复杂度就是 1+2+3+…+n, 所以时间复杂度就是O(n^2)

//快速排序
void QuickSrot(int* a, int begin, int end)
{//当只有一个元素就不用进行了if (begin >= end)return;int key = begin;int left = begin;//这里不能begin加1 否则在遇到有序的时候就会排序出错int right = end;while (left < right){// 找最小while (left < right){if (a[right] < a[key]){break;}right--;}// 找最大while (left < right){if (a[left] > a[key]){break;}left++;}excheng(&a[right], &a[left]);}excheng(&a[right], &a[key]);//左QuickSrot(a, begin, right - 1);// 右QuickSrot(a, right + 1, end);
}

优化点

三数取中

思路:
我们可以在数组的前后和中间选取中位数,然后把中位数和开头进行交换,

int TriNum(int *a,int begin, int end)
{int mid = (begin - end) / 2 + end;if (begin > end){if (end > mid){return end;}else if(begin < mid){return begin;}return mid;}else{if (begin > mid){return begin;}else if (end < mid){return end;}elsereturn mid;}
}
//快速排序
void QuickSrot(int* a, int begin, int end)
{//当只有一个元素就不用进行了if (begin >= end)return;//三数取中int key = 0;key = TriNum(a, begin, end);exchange(&a[begin], &a[key]);key = begin;int left = begin;int right = end;//普通方法//int key = begin;//int left = begin;//这里不能begin加1 否则在遇到有序的时候就会排序出错//int right = end;while (left < right){// 找最小while (left < right){if (a[right] < a[key]){break;}right--;}// 找最大while (left < right){if (a[left] > a[key]){break;}left++;}excheng(&a[right], &a[left]);}excheng(&a[right], &a[key]);//左QuickSrot(a, begin, right - 1);// 右QuickSrot(a, right + 1, end);
}

小区间优化

当我们在使用快速排序的时候，一直排序知道递归到还剩下该数组的10%的数没有排序，我们如果使用递归就很对栈的空间浪费很大。那我们可以选择使用插入排序，

//快速排序
void QuickSrot(int* a, int begin, int end)
{//当只有一个元素就不用进行了if (begin >= end)return;if (end - begin  + 1 <= 10){//插入排序InsertSort(a + begin, end - begin + 1);//我们要清楚要从哪里开始插入排序}else{//三数取中int key = 0;key = TriNum(a, begin, end);excheng(&a[begin], &a[key]);key = begin;int left = begin;int right = end;//普通方法,有可能会栈溢出//int key = begin;//int left = begin;//这里不能begin加1 否则在遇到有序的时候就会排序出错//int right = end;while (left < right){// 找最小while (left < right){if (a[right] < a[key]){break;}right--;}// 找最大while (left < right){if (a[left] > a[key]){break;}left++;}excheng(&a[right], &a[left]);}excheng(&a[right], &a[key]);//左QuickSrot(a, begin, right - 1);// 右QuickSrot(a, right + 1, end);}}

挖坑法

在这里插入图片描述

//挖坑法
void QuickSrot2(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{//三数取中int key = TriNum(a, begin, end);excheng(&a[key], &a[begin]);//坑key = begin;int num = a[key];int left = begin;int right = end;while (left < right){//找小while (left < right){if (a[right] < num){a[key] = a[right];key = right;break;}right--;}//找大while (left < right){if (a[left] > num){a[key] = a[left];key = left;break;}left++;}}a[key] = num;//左QuickSrot(a, begin, right - 1);// 右QuickSrot(a, right + 1, end);}}

前后指针版本

在这里插入图片描述
思路:
cur遇见比key大的值,cur++
cur遇见比key小的值,prev++,交换prev和cur的值交换,然后cur++
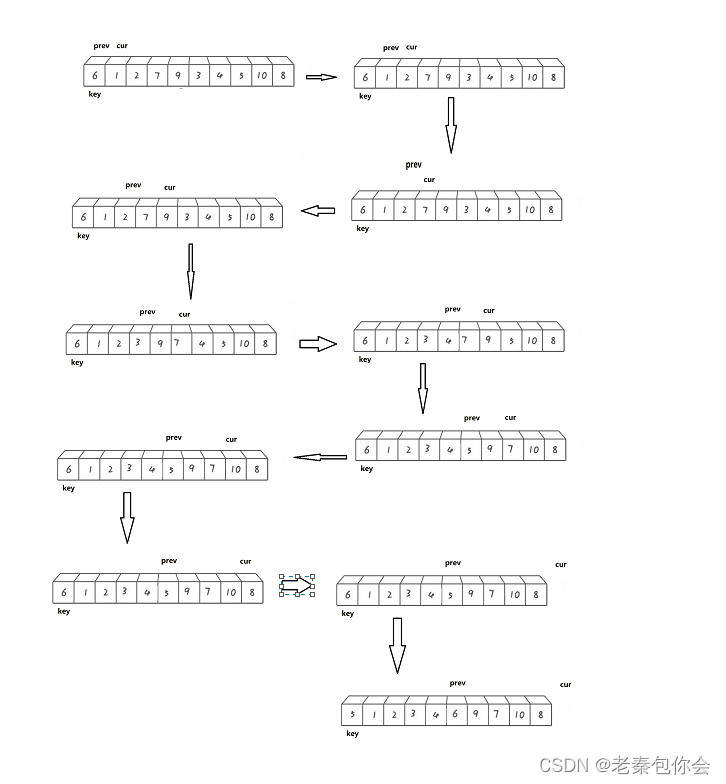
在这里插入图片描述

//前后指针版本
// 快速排序版本3
void QuickSrot3(int* a, int begin, int end)
{if (begin >= end)return;int key = TriNum(a, begin, end);excheng(&a[key], &a[begin]);key = begin;int prev = begin;int cur = begin + 1;while (cur <= end){//cur 比较if (a[cur] < a[key] && ++prev != cur)//增加++prev != cur可以有效解决相同位置进行交换{exchange(&a[cur], &a[prev]);}cur++;}exchange(&a[key], &a[prev]);//左QuickSrot(a, begin, prev - 1);// 右QuickSrot(a, prev + 1, end);
}

疑惑

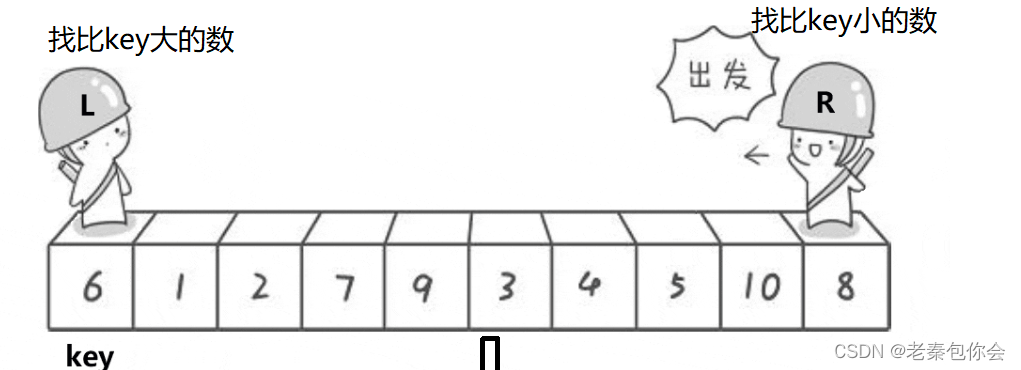
在这里插入图片描述

  1. 为什么相遇位置比key小
    原因:是right先走
    两种情况:
    (1).R遇见L —>(L和R交换后,R先走)R没有找到比key小的,一直走,直到R遇见L,(特殊情况除外)
    (2)L遇见R----->(R找到小了),然后L没有找到比key大的,一直走,直到L遇见R,(特殊情况除外)

这篇关于数据结构第六课 -----排序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/485853。

相关文章

【数据结构】线性表：顺序表

【数据结构】线性表：顺序表

文章目录 1. 线性表2. 顺序表2.1 概念及结构2.2 接口实现2.3 顺序表的问题及思考 1. 线性表 线性表是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串… 线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式
阅读更多...
数据结构9——排序

数据结构9——排序

一、冒泡排序 冒泡排序（Bubble Sort），顾名思义，就是指越小的元素会经由交换慢慢“浮”到数列的顶端。 算法原理 从左到右，依次比较相邻的元素大小，更大的元素交换到右边；从第一组相邻元素比较到最后一组相邻元素，这一步结束最后一个元素必然是参与比较的元素中最大的元素；按照大的居右原则，重新从左到后比较，前一轮中得到的最后一个元素不参4与比较，得出新一轮的最大元素；按照上述规则，每一轮结
阅读更多...
七种排序方式总结

七种排序方式总结

/*2018.01.23*A:YUAN*T:其中排序算法：冒泡排序，简单排序，直接插入排序，希尔排序，堆排序，归并排序，快速排序*/#include <stdio.h>#include <math.h>#include <malloc.h>#define MAXSIZE 10000#define FALSE 0#define TRUE 1typedef struct {i
阅读更多...
拓扑排序——C语言

拓扑排序——C语言

拓扑排序（Topological Sorting）是一种用于有向无环图（DAG）的排序算法，其输出是图中所有顶点的线性排序，使得对于每条有向边 (u, v)，顶点 u 在 v 之前出现。拓扑排序确定了项目网络图中的起始事件和终止事件，也就是顶点的执行顺序。         因为是有向无环图，所以拓扑排序的作用其实就是把先发生的排序在前面，后发生的排序到后面。 例如现在我们有一个
阅读更多...
算法与数据结构面试宝典——回溯算法详解（C#，C++）

算法与数据结构面试宝典——回溯算法详解（C#，C++）

文章目录 1. 回溯算法的定义及应用场景2. 回溯算法的基本思想3. 递推关系式与回溯算法的建立4. 状态转移方法5. 边界条件与结束条件6. 算法的具体实现过程7. 回溯算法在C#，C++中的实际应用案例C#示例C++示例 8. 总结回溯算法的主要特点与应用价值 回溯算法是一种通过尝试各种可能的组合来找到所有解的算法。这种算法通常用于解决组合问题，如排列、组合、棋盘游
阅读更多...
嵌入式学习——数据结构（哈希、排序）——day50

嵌入式学习——数据结构（哈希、排序）——day50

1. 查找二叉树、搜索二叉树、平衡二叉树 2. 哈希表——人的身份证——哈希函数 3. 哈希冲突、哈希矛盾 4. 哈希代码 4.1 创建哈希表 4.2  5. 算法设计 5.1 正确性 5.2 可读性（高内聚、低耦合） 5.3 健壮性 5.4 高效率（时间复杂度）时间复杂度越低，效率越高， 5.5 低储存（空间复杂度）空间复杂度越低，存储空间越少 6.排序算法 6.1 冒
阅读更多...
【数据结构与算法 经典例题】使用队列实现栈（图文详解）

【数据结构与算法 经典例题】使用队列实现栈（图文详解）

💓 博客主页：倔强的石头的CSDN主页               📝Gitee主页：倔强的石头的gitee主页    ⏩ 文章专栏：《数据结构与算法 经典例题》C语言                                   期待您的关注 ​​ 目录  一、问题描述 二、前置知识 三、解题思路 四、C语言实现代码 🍃队列实现代码：
阅读更多...
数据结构：二叉树详解 c++信息学奥赛基础知识讲解

数据结构：二叉树详解 c++信息学奥赛基础知识讲解

目录 一、二叉树的定义 二、二叉树的形态 三、二叉树的性质 四、二叉树的存储 五、二叉树的创建与遍历（递归） 六、二叉树实现 创建二叉树 展示二叉树 1、计算数的高度 2、计算数的叶子数量 3、计算数的宽度 4、层次遍历 5、前序遍历 递归写法 非递归写法 6、中序遍历 递归写法 非递归写法 7、后序遍历 递归写法 非递归写法 8、输出根节点到所有叶
阅读更多...
Java数据结构4-链表

Java数据结构4-链表

1. ArrayList的缺陷 由于其底层是一段连续空间，当在ArrayList任意位置插入或者删除元素时，就需要将后序元素整体往前或者往后搬移，时间复杂度为O(n)，效率比较低，因此ArrayList不适合做任意位置插入和删除比较多的场景。因此：java集合中又引入了LinkedList，即链表结构。 2. 链表 2.1 链表的概念及结构 链表是一种物理存储结构上非连续存储结构，数据元素
阅读更多...
大学生自救数据结构与算法（py实现）——01递归

大学生自救数据结构与算法（py实现）——01递归

目录 目录 递归 基本概念 工作原理 基本要素 优点 缺点 实现技巧 实例解析：计算阶乘 斐波那契数列 高效的斐波那契数列 python中的最大递归深度 二分查找 基本原理 性能分析 优化与变体 线性递归  元素序列的递归求和 二路递归 二路递归的基本概念 典型应用 工作原理 多重递归  示例：计算卡特兰数（Catalan Number） 尾递
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2