模糊控制算法的C++实现

2023-12-12 17:08
文章标签 算法 c++ 实现 模糊控制

本文主要是介绍模糊控制算法的C++实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

之前写过一篇关于使用样本数据获取模糊规则的博文，原文 的地址是：http://blog.csdn.net/shuoyueqishilove/article/details/71908410，大家可以参考，本篇文章适合对模糊控制算法有一定了解的人阅读，给大家提供一种如何用C++实现模糊控制的方法，仅供参考。
实现模糊控制器需要以下步骤：

  1. 确定模糊控制器的输入和输出量
  2. 设计模糊控制器的控制规则
  3. 确立模糊化和非模糊化的方法
  4. 选择模糊控制器的输入变量和输出变量的论域并确定模糊控制器的参数（如量化因子，比例因子等）
  5. 编制模糊控制算法的应用程序
  6. 合理选择模糊控制算法的采样时间

本模糊控制器采用双输入单输出的形式，输入变量为误差e和误差的变化率de,输出为控制量u；e,de,u的量化论域范围为[-3,-2,-1,0,1,2,3],划分的模糊子集为：[NB,NM,NS,ZO,PS,PM,PB].基本论域的范围选取需要根据实际情况来确定上限值emax,demax,umax.
量化因子:Ke=3/emax, Kde=3/demax,
输出缩放因子：Ku=umax/3
为了减少计算量，e,de,u的隶属度函数都选用三角形隶属度函数。如下图所示：
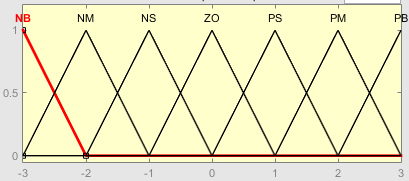
模糊集合划分
模糊控制最重要的是要确定模糊控制规则，它可以通过专家经验获得，也可以通过采样数据获得，这里使用的模糊控制规则表如下；
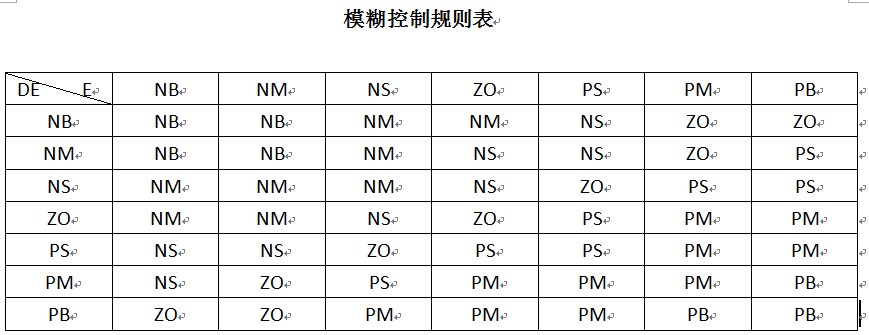
控制规则表
在微处理器中实现模糊控制的一般采用离线查表的方法。首先模糊化输入到控制器中的e和de，计算他们的在每个模糊子集中的隶属度值，然后找出激活的模糊子集，存储起来，最后使用加权平均的方法计算输出值。具体的公式如下：
公式1
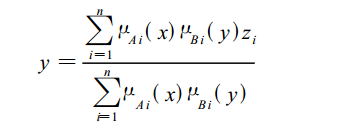
Zi为u的模糊隶属度函数的尖点所对应的横坐标值。
下面讲讲怎么用C++实现模糊控制器。
首先需要建立一个Fuzzy_controller的类：

class Fuzzy_controller
{
public:const static int N=7;//定义量化论域模糊子集的个数
private:float target;//系统的控制目标float actual;//采样获得的实际值float e;     //误差float e_pre; //上一次的误差float de;    //误差的变化率float emax;  //误差基本论域上限float demax; //误差辩化率基本论域的上限float umax;  //输出的上限float Ke;    //Ke=n/emax,量化论域为[-3,-2,-1,0,1,2,3]float Kde;   //Ke=n/demax,量化论域为[-3,-2,-1,0,1,2,3]float Ku;    //Ke=umax/n,量化论域为[-3,-2,-1,0,1,2,3]int rule[N][N];//模糊规则表string mf_t_e;   //e的隶属度函数类型string mf_t_de;  //de的隶属度函数类型string mf_t_u;   //u的隶属度函数类型float *e_mf_paras; //误差的隶属度函数的参数float *de_mf_paras;//误差的偏差隶属度函数的参数float *u_mf_paras; //输出的隶属度函数的参数public:Fuzzy_controller(float e_max,float de_max,float u_max);~Fuzzy_controller();float trimf(float x,float a,float b,float c);          //三角隶属度函数float gaussmf(float x,float ave,float sigma);          //正态隶属度函数float trapmf(float x,float a,float b,float c,float d); //梯形隶属度函数//设置模糊隶属度函数的参数void setMf(const string & mf_type_e,float *e_mf,const string & mf_type_de,float *de_mf,const string & mf_type_u,float *u_mf);void setRule(int rulelist[N][N]);                          //设置模糊规则float realize(float t,float a);              //实现模糊控制void showInfo();                                      //显示该模糊控制器的信息void showMf(const string & type,float *mf_paras);      //显示隶属度函数的信息
};

然后给出类方法的定义：

Fuzzy_controller::Fuzzy_controller(float e_max,float de_max,float u_max):
target(0),actual(0),emax(e_max),demax(de_max),umax(u_max),e_mf_paras(NULL),de_mf_paras(NULL),u_mf_paras(NULL)
{e=target-actual;e_pre=0;de=e-e_pre;Ke=(N/2)/emax;Kde=(N/2)/demax;Ku=umax/(N/2);mf_t_e="trimf";mf_t_de="trimf";mf_t_u="trimf";
}Fuzzy_controller::~Fuzzy_controller()
{delete [] e_mf_paras;delete [] de_mf_paras;delete [] u_mf_paras;
}
//三角隶属度函数
float Fuzzy_controller::trimf(float x,float a,float b,float c)
{float u;if(x>=a&&x<=b)u=(x-a)/(b-a);else if(x>b&&x<=c)u=(c-x)/(c-b);elseu=0.0;return u;}
//正态隶属度函数
float Fuzzy_controller::gaussmf(float x,float ave,float sigma) 
{float u;if(sigma<0){cout<<"In gaussmf, sigma must larger than 0"<<endl;}u=exp(-pow(((x-ave)/sigma),2));return u;
}
//梯形隶属度函数
float Fuzzy_controller::trapmf(float x,float a,float b,float c,float d)
{float u;if(x>=a&&x<b)u=(x-a)/(b-a);else if(x>=b&&x<c)u=1;else if(x>=c&&x<=d)u=(d-x)/(d-c);elseu=0;return u;
}
//设置模糊规则
void Fuzzy_controller::setRule(int rulelist[N][N])
{for(int i=0;i<N;i++)for(int j=0;j<N;j++)rule[i][j]=rulelist[i][j];
}//设置模糊隶属度函数的类型和参数
void Fuzzy_controller::setMf(const string & mf_type_e,float *e_mf,const string & mf_type_de,float *de_mf,const string & mf_type_u,float *u_mf)
{if(mf_type_e=="trimf"||mf_type_e=="gaussmf"||mf_type_e=="trapmf")mf_t_e=mf_type_e;elsecout<<"Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\""<<endl;if(mf_type_de=="trimf"||mf_type_de=="gaussmf"||mf_type_de=="trapmf")mf_t_de=mf_type_de;elsecout<<"Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\""<<endl;if(mf_type_u=="trimf"||mf_type_u=="gaussmf"||mf_type_u=="trapmf")mf_t_u=mf_type_u;elsecout<<"Type of membership function must be \"trimf\" or \"gaussmf\" or \"trapmf\""<<endl;e_mf_paras=new float [N*3];de_mf_paras=new float [N*3];u_mf_paras=new float [N*3];for(int i=0;i<N*3;i++)e_mf_paras[i]=e_mf[i];for(int i=0;i<N*3;i++)de_mf_paras[i]=de_mf[i];for(int i=0;i<N*3;i++)u_mf_paras[i]=u_mf[i];
}
//实现模糊控制
float Fuzzy_controller::realize(float t,float a)   
{float u_e[N],u_de[N],u_u[N];int u_e_index[3],u_de_index[3];//假设一个输入最多激活3个模糊子集float u;int M;target=t;actual=a;e=target-actual;de=e-e_pre;e=Ke*e;de=Kde*de;if(mf_t_e=="trimf")M=3;               //三角函数有三个参数else if(mf_t_e=="gaussmf")M=2;              //正态函数有两个参数else if(mf_t_e=="trapmf")M=4;              //梯形函数有四个参数int j=0;for(int i=0;i<N;i++){u_e[i]=trimf(e,e_mf_paras[i*M],e_mf_paras[i*M+1],e_mf_paras[i*M+2]);//e模糊化，计算它的隶属度if(u_e[i]!=0)u_e_index[j++]=i;                                              //存储被激活的模糊子集的下标，可以减小计算量}for(;j<3;j++)u_e_index[j]=0;if(mf_t_e=="trimf")M=3;              //三角函数有三个参数else if(mf_t_e=="gaussmf")M=2;              //正态函数有两个参数else if(mf_t_e=="trapmf")M=4;               //梯形函数有四个参数j=0;for(int i=0;i<N;i++){u_de[i]=trimf(de,de_mf_paras[i*M],de_mf_paras[i*M+1],de_mf_paras[i*M+2]);//de模糊化，计算它的隶属度if(u_de[i]!=0)u_de_index[j++]=i;                                                    //存储被激活的模糊子集的下标，可以减小计算量}for(;j<3;j++)u_de_index[j]=0;float den=0,num=0;for(int m=0;m<3;m++)for(int n=0;n<3;n++){num+=u_e[u_e_index[m]]*u_de[u_de_index[n]]*rule[u_e_index[m]][u_de_index[n]];den+=u_e[u_e_index[m]]*u_de[u_de_index[n]];}u=num/den;u=Ku*u;if(u>=umax)   u=umax;else if(u<=-umax)  u=-umax;e_pre=e;return u;
}
void Fuzzy_controller::showMf(const string & type,float *mf_paras)
{int tab;if(type=="trimf")tab=2;else if(type=="gaussmf")tab==1;else if(type=="trapmf")tab=3;cout<<"函数类型："<<mf_t_e<<endl;cout<<"函数参数列表："<<endl;float *p=mf_paras;for(int i=0;i<N*(tab+1);i++){cout.width(3);cout<<p[i]<<"  ";if(i%3==tab)cout<<endl;}
}
void Fuzzy_controller::showInfo()
{cout<<"Info of this fuzzy controller is as following:"<<endl;cout<<"基本论域e：["<<-emax<<","<<emax<<"]"<<endl;cout<<"基本论域de：["<<-demax<<","<<demax<<"]"<<endl;cout<<"基本论域u：["<<-umax<<","<<umax<<"]"<<endl;cout<<"误差e的模糊隶属度函数参数："<<endl;showMf(mf_t_e,e_mf_paras);cout<<"误差变化率de的模糊隶属度函数参数："<<endl;showMf(mf_t_de,de_mf_paras);cout<<"输出u的模糊隶属度函数参数："<<endl;showMf(mf_t_u,u_mf_paras);cout<<"模糊规则表："<<endl;for(int i=0;i<N;i++){for(int j=0;j<N;j++){cout.width(3);cout<<rule[i][j]<<"  ";}cout<<endl;}cout<<endl;cout<<"误差的量化比例因子Ke="<<Ke<<endl;cout<<"误差变化率的量化比例因子Kde="<<Kde<<endl;cout<<"输出的量化比例因子Ku="<<Ku<<endl;cout<<"设定目标target="<<target<<endl;cout<<"误差e="<<e<<endl;cout<<endl;
}

此模糊控制的类，允许用户使用不同的模糊隶属度函数，如三角型，正态分布型和梯形。但是需要相应的给出适当的函数参数。用户可以修改模糊控制规则表，以提高模糊控制器的性能。但是用户需要首先明确误差e，误差变化率de和输出u的最大范围，因为这里需要依据他们来确定量化因子和缩放因子，如果给出的范围不合适，则很难达到理想的控制效果。
下面是一个测试的例子，仅供参考：

#include<iostream>
#include"fuzzy_controller.h"
#define NB -3
#define NM -2
#define NS -1
#define ZO 0
#define PS 1
#define PM 2
#define PB 3int main()
{float target=600;float actual=0;float u=0;int ruleMatrix[7][7]={{NB,NB,NM,NM,NS,ZO,ZO},{NB,NB,NM,NS,NS,ZO,PS},{NM,NM,NM,NS,ZO,PS,PS},{NM,NM,NS,ZO,PS,PM,PM},{NS,NS,ZO,PS,PS,PM,PM},{NS,ZO,PS,PM,PM,PM,PB},{ZO,ZO,PM,PM,PM,PB,PB}};//模糊规则表float e_mf_paras[21]={-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};//误差e的隶属度函数参数，这里隶属度函数为三角型，所以3个数据为一组float de_mf_paras[21]={-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};//误差变化率de的模糊隶属度函数参数float u_mf_paras[21]={-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};//输出量u的隶属度函数参数Fuzzy_controller fuzzy(1000,650,500);//控制器初始化，设定误差，误差变化率，输出的最大值fuzzy.setMf("trimf",e_mf_paras,"trimf",de_mf_paras,"trimf",u_mf_paras);//设定模糊隶属度函数fuzzy.setRule(ruleMatrix);//设定模糊规则cout<<"num   target    actual"<<endl;for(int i=0;i<100;i++){u=fuzzy.realize(target,actual);actual+=u;cout<<i<<"      "<<target<<"      "<<actual<<endl;}fuzzy.showInfo();system("pause");return 0;
}

运行结果：
结果
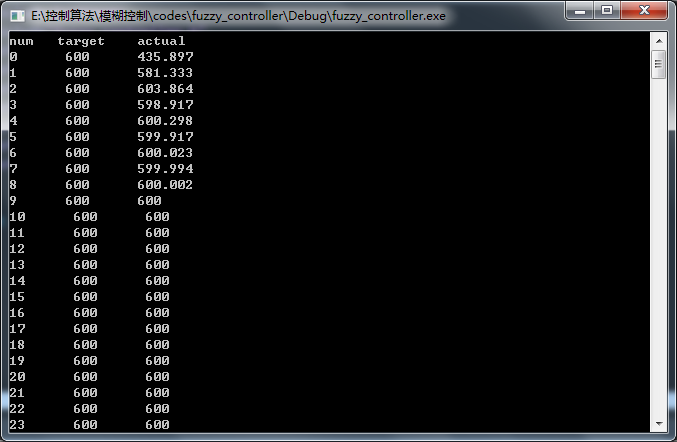
这里设定的目标值为600,可见，控制器在运行到9次时就稳定在了600,控制效果比较好。
代码已上传至我的CSDN，有兴趣的可以下载看看：
https://download.csdn.net/download/shuoyueqishilove/10433961

这篇关于模糊控制算法的C++实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/485341。

相关文章

python实现svg图片转换为png和gif

python实现svg图片转换为png和gif

《python实现svg图片转换为png和gif》这篇文章主要为大家详细介绍了python如何实现将svg图片格式转换为png和gif,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录python实现svg图片转换为png和gifpython实现图片格式之间的相互转换延展：基于Py
阅读更多...
Python利用ElementTree实现快速解析XML文件

Python利用ElementTree实现快速解析XML文件

《Python利用ElementTree实现快速解析XML文件》ElementTree是Python标准库的一部分,而且是Python标准库中用于解析和操作XML数据的模块,下面小编就来和大家详细讲讲... 目录一、XML文件解析到底有多重要二、ElementTree快速入门1. 加载XML的两种方式2.
阅读更多...
Java的栈与队列实现代码解析

Java的栈与队列实现代码解析

《Java的栈与队列实现代码解析》栈是常见的线性数据结构,栈的特点是以先进后出的形式,后进先出,先进后出,分为栈底和栈顶,栈应用于内存的分配,表达式求值,存储临时的数据和方法的调用等,本文给大家介绍J... 目录栈的概念（Stack）栈的实现代码队列（Queue）模拟实现队列(双链表实现)循环队列（循环数组
阅读更多...
C++如何通过Qt反射机制实现数据类序列化

C++如何通过Qt反射机制实现数据类序列化

《C++如何通过Qt反射机制实现数据类序列化》在C++工程中经常需要使用数据类,并对数据类进行存储、打印、调试等操作,所以本文就来聊聊C++如何通过Qt反射机制实现数据类序列化吧... 目录设计预期设计思路代码实现使用方法在 C++ 工程中经常需要使用数据类，并对数据类进行存储、打印、调试等操作。由于数据类
阅读更多...
Python实现图片分割的多种方法总结

Python实现图片分割的多种方法总结

《Python实现图片分割的多种方法总结》图片分割是图像处理中的一个重要任务,它的目标是将图像划分为多个区域或者对象,本文为大家整理了一些常用的分割方法,大家可以根据需求自行选择... 目录1. 基于传统图像处理的分割方法(1) 使用固定阈值分割图片(2) 自适应阈值分割(3) 使用图像边缘检测分割(4)
阅读更多...
Android实现在线预览office文档的示例详解

Android实现在线预览office文档的示例详解

《Android实现在线预览office文档的示例详解》在移动端展示在线Office文档（如Word、Excel、PPT）是一项常见需求,这篇文章为大家重点介绍了两种方案的实现方法,希望对大家有一定的... 目录一、项目概述二、相关技术知识三、实现思路3.1 方案一：WebView + Office Onl
阅读更多...
C# foreach 循环中获取索引的实现方式

C# foreach 循环中获取索引的实现方式

《C#foreach循环中获取索引的实现方式》：本文主要介绍C#foreach循环中获取索引的实现方式,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友参考下吧... 目录一、手动维护索引变量二、LINQ Select + 元组解构三、扩展方法封装索引四、使用 for 循环替代
阅读更多...
Spring Security+JWT如何实现前后端分离权限控制

Spring Security+JWT如何实现前后端分离权限控制

《SpringSecurity+JWT如何实现前后端分离权限控制》本篇将手把手教你用SpringSecurity+JWT搭建一套完整的登录认证与权限控制体系,具有很好的参考价值,希望对大家... 目录Spring Security+JWT实现前后端分离权限控制实战一、为什么要用 JWT？二、JWT 基本结构
阅读更多...
Java实现优雅日期处理的方案详解

Java实现优雅日期处理的方案详解

《Java实现优雅日期处理的方案详解》在我们的日常工作中,需要经常处理各种格式,各种类似的的日期或者时间,下面我们就来看看如何使用java处理这样的日期问题吧,感兴趣的小伙伴可以跟随小编一起学习一下... 目录前言一、日期的坑1.1 日期格式化陷阱1.2 时区转换二、优雅方案的进阶之路2.1 线程安全重构2
阅读更多...
Android实现两台手机屏幕共享和远程控制功能

Android实现两台手机屏幕共享和远程控制功能

《Android实现两台手机屏幕共享和远程控制功能》在远程协助、在线教学、技术支持等多种场景下,实时获得另一部移动设备的屏幕画面,并对其进行操作,具有极高的应用价值,本项目旨在实现两台Android手... 目录一、项目概述二、相关知识2.1 MediaProjection API2.2 Socket 网络
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2