本文主要是介绍博弈论(二): 车联网环境下一个基于 博弈论的十字路口智能 交通控制算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 问题描述
1、胆小鬼博弈

胆小鬼博弈(The game of chicken)又译懦夫博弈,是博弈论中一个影响深远的模型,逻辑就是“不要命的最大”。模型中,两名车手相对驱车而行,谁最先转弯的一方被耻笑为“胆小鬼”(chicken),让另一方胜出,因此这博弈模型在英文 中 称 为 The Game of Chicken(懦夫游戏),但如果两人拒绝转弯,任由两车相撞,最终谁都无法受益。其收益矩阵如图.1 所示。本方法受胆小鬼博弈启发。

该博弈只有两名玩家,#1决定车辆 2 和 4 的动作,而#2决定
车辆 1 和 3 的动作,如图 2 所示。每个玩家想要以这样的方式控制车辆以最小化它们在交叉路口的延迟并保证它们安全地(未发生碰撞)穿过十字路口。
每个玩家最三种可能的动作:加速(表示为1),减速(表示为−1)或以当前速度继续行驶(表示为0)。由于每个玩家有两辆车并且每辆车都有动作组,因此
玩家的动作是车辆动作的笛卡尔乘积。每辆汽车可以采取的动作是{1, 0,−1}, 则 每个 玩家 可 以 采 取 的 动 作 有 9 种,即 { 1 , 0 , −1 }×{ 1 , 0 , −1 } =
{ (1,1), (1,0) , (0,1) , (1, −1) , (−1,1), (0,0) , (0, −1) , (−1,0) , (−1, −1) } ,例如
#1的动作为(1,0)代表他命令 2 号车加速,3 号车保持当前速度行驶。
- 在给定车辆数据与玩家策略后可以运行驾驶模拟

3.1数据:
道路结构如图 3 所示。每次模拟中随机生成 4 辆车的数据,每辆车的数据的形式为(d, v),如图所示,为车辆距离停车线stop _line 的距离,范围为[0,90],v为车辆的当前速度,初始化范围为[20,40],规则是加速后速度不能超过40,减速下限无限制。
3.2根据车辆动作速度更新:
为简化计算过程,实验中加速(action = 1)直接将原速度提高 40%,减速(action = −1)直接将原速度减少 40%,保持当前速度则速度不变。速度的更新公式为:
3.3碰撞判定:
以图3中4号碰撞点为例,计算3号车与4号车到达碰撞点4的时间差,如时间差小于1s则判定为碰撞,否则判定为通过。
3.4博弈损失(通行时间)
一次模拟中 4 个碰撞点中有一个发生了碰撞则为博弈中双输的情况,该次博弈损失为无穷大( inf )。如未发生碰撞,则博弈损失为 4 辆车通过该十字路口的平均时间。一辆车( d, v )的通行时间为:
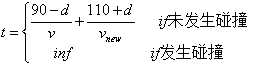
此处假设车辆经过一次速度调整后,在驶出路口前不再调整速度。
4.1计算博弈损失矩阵
遍历所有的决策组合,计算出博弈损失矩阵(通行时间),并给出最快通过时的玩家的决策:
|
| (1, 1) | (1, 0) | (1, -1) | (0, 1) | (0, 0) | (0, -1) | (-1, 1) | (-1, 0) | (-1, -1) |
| (1, 1) |
|
|
|
|
|
|
|
|
|
| (1, 0) |
|
|
|
|
|
|
|
|
|
| (1, -1) |
|
|
|
|
|
|
|
|
|
| (0, 1) |
|
|
|
|
|
|
|
|
|
| (0, 0) |
|
|
|
|
|
|
|
|
|
| (0, -1) |
|
|
|
|
|
|
|
|
|
| (-1, 1) |
|
|
|
|
|
|
|
|
|
| (-1, 0) |
|
|
|
|
|
|
|
|
|
| (-1, -1) |
|
|
|
|
|
|
|
|
|
通行时间最短:
Player #1 采取的策略 :
Player #2 采取的策略 :
4.2与传统方法对比
传统方法:先截断一个方向的车流,让另一个方向的车全部通行后在开流。例如先让车 2,4 通行,后让 1,3 通行。通行时间为

每次实验中,随机生成 4 辆车的数据,计算该数据在传统方法下的通行时间,再计算 4.1 中的矩阵,以矩阵中的最小值为博弈方法的通行时间。
进行 10 次实验,分别记录 10 次实验中博弈方法和传统方法的结果,书写实验报告。
- 实验结果
遍历所有的决策组合,计算出博弈损失矩阵(通行时间),并给出最快通过时的玩家的决策:
|
| (1, 1) | (1, 0) | (1, -1) | (0, 1) | (0, 0) | (0, -1) | (-1, 1) | (-1, 0) | (-1, -1) |
| (1, 1) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (1, 0) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (1, -1) | inf | inf | 7.3 | inf | inf | 7.7 | inf | inf | inf |
| (0, 1) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (0, 0) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (0, -1) | inf | inf | 7.5 | inf | inf | 7.9 | inf | inf | inf |
| (-1, 1) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (-1, 0) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| (-1, -1) | inf | inf | inf | inf | inf | inf | inf | inf | inf |
通行时间最短: 7.3s
Player #1 采取的策略 :[1, -1]
Player #2 采取的策略 :[1, -1]
传统时间: 13.7s
重复十次实验
|
| 最短通行时间 | 传统时间 |
| 1 | [[-1, 1], [1, 1]] 8.04 | 18.85 |
| 2 | [[1, 1], [0, 0]] 6.34 | 16.53 |
| 3 | [[0, -1], [1, -1]] 8.38 | 14.84 |
| 4 | [[0, 0], [0, 1]] 6.56 | 15.90 |
| 5 | [[-1, 0], [1, 1]] 6.23 | 13.52 |
| 6 | [[1, 1], [0, -1]] 7.57 | 17.08 |
| 7 | All accident | 17.25 |
| 8 | All accident | 15.90 |
| 9 | [[-1, 0], [1, 1]] 6.20 | 14.16 |
| 10 | All accident | 11.78 |
- 代码展示
import random
# 初始化一辆车
def init():v = random.uniform(20, 40)d = random.uniform(0, 90)return [d, v, 0]def cal_time(car):return (90-car[0])/car[1] + (110+car[0])/car[2]def tradition(car):car1, car2, car3, car4 = carreturn max(200/car1[1], 200/car3[1]) + max(200/car2[1], 200/car4[1])def game_run(player1, player2, car):# 初始化车辆car1, car2, car3, car4 = car# 速度更新car1[2] = car1[1] * (1 + player2[0] * 0.4)car2[2] = car2[1] * (1 + player1[0] * 0.4)car3[2] = car3[1] * (1 + player2[1] * 0.4)car4[2] = car4[1] * (1 + player1[1] * 0.4)# 碰撞分析accident = any([abs((car4[0] + 15) / car4[2] - (car1[0] + 5) / car1[2]) < 1, abs((car1[0] + 15) / car1[2] - (car2[0] + 5) / car2[2]) < 1, abs((car2[0] + 15) / car2[2] - (car3[0] + 5) / car3[2]) < 1, abs((car3[0] + 15) / car3[2] - (car4[0] + 5) / car4[2]) < 1]) return (cal_time(car1) + cal_time(car2) + cal_time(car3) + cal_time(car4)) / 4 + accident * 9999999def main():# 设置玩家行动# player1 = [1, 1] # player2 = [1, 1] action = [[1, 1], [1, 0], [1, -1], [0, 1], [0, 0], [0, -1], [-1, 1], [-1, 0], [-1, 1]]car = [init(), init(), init(), init()]print("init car:", car)min_t = 999min_t_action = Nonefor i in range(9):for j in range(9):t = game_run(action[i], action[j], car) # run(player1, player2)if t < 9999999:print("%.1f" % t, end=" ")if t < min_t:min_t = tmin_t_action = [action[i], action[j]]else:print("inf", end=" ")print()if min_t_action:print("min of game: ", min_t_action, "%.1f" % min_t)else:print("min of game: accident")print("tradition time: ", "%.1f" % tradition(car))if __name__ == "__main__":main()
这篇关于博弈论(二): 车联网环境下一个基于 博弈论的十字路口智能 交通控制算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









