本文主要是介绍博弈论(一) :极小节点覆盖,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 问题描述
可以验证:当雪堆博弈满足时,网络博弈的纳什均衡中的采用合作策略的节点构成极小节点覆盖。(自己编程序验证这个结论,网络自定,节点数目不少于 10)。
- 基本原理

- 实验结果
1、网络结构
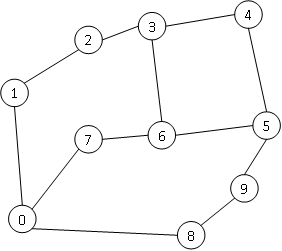
2、邻接矩阵
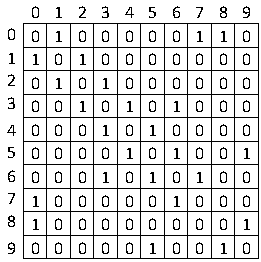
上表是该网络的邻接矩阵,0 表示不相邻,1 表示两个节点相邻。我们用一个矩阵 S 表示每个节点的策略集合。S=[1,0,1,0,1,0,1,0,0,0]
3、实验结果
S = [1 0 1 0 1 0 1 0 0 1]是该网络的极小覆盖。
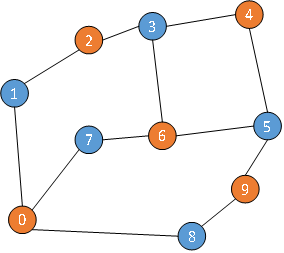
上图中红色表示选择合作策略,且所有红色节点构成极小节点覆盖。数字是每个节点的标号。
- 代码展示
import numpy as np
# 邻接矩阵
adj_matrix = np.array([[0, 1, 0, 0, 0, 0, 0, 1, 1, 0],[1, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 1, 0, 1, 0, 0, 1, 0, 0, 0],[0, 0, 1, 0, 1, 0, 0, 0, 0, 0],[0, 0, 0, 1, 0, 1, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 1, 0, 0, 0],[0, 0, 1, 0, 0, 1, 0, 1, 0, 1],[1, 0, 0, 0, 0, 0, 1, 0, 0, 0],[1, 0, 0, 0, 0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 0, 1, 0, 1, 0]])
b_C = np.zeros(10) # 当选取合作策略时的收益矩阵
b_D = np.zeros(10) # 当选取背叛策略时的收益矩阵
r = 0.1
s = np.array([1, 0, 0, 0, 1, 0, 1, 0, 1, 1]) # 初始化策略集合
adj_list = []
for i in range(10): # 统计每个节点邻点的标号list = []for j in range(len(adj_matrix[i])):if adj_matrix[i][j] == 1:list.append(j)adj_list.append(list)while (True):s_last = s.copy() # 保存上一次迭代的结果for i in range(len(s)):num_C = 0;num_D = 0for j in range(len(adj_list[i])):# 统计第 i 个节点邻点中合作性的节点个数 num_C# 以及背叛性的节点个数 num_Dif s[adj_list[i][j]] == 1:num_C += 1else:num_D += 1# 计算第 i 个节点取两种不同策略时的收益b_C[i] = num_C + num_D * (1 - r)b_D[i] = num_C * (1 + r)if b_C[i] > b_D[i]:s[i] = 1else:s[i] = 0if (s == s_last).all(): # 若本次迭代结果与上次一样则停止迭代输出结果print(s)break
这篇关于博弈论(一) :极小节点覆盖的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






