ACwing217. 绿豆蛙的归宿 218. 扑克牌

217. 绿豆蛙的归宿

题意：

给出一个有向无环的连通图，起点为 1，终点为 N，每条边都有一个长度。

数据保证从起点出发能够到达图中所有的点，图中所有的点也都能够到达终点。

绿豆蛙从起点出发，走向终点。

到达每一个顶点时，如果有 K 条离开该点的道路，绿豆蛙可以选择任意一条道路离开该点，并且走向每条路的概率为 1/K。

现在绿豆蛙想知道，从起点走到终点所经过的路径总长度的期望是多少？

分析：
求期望一般都用dp，不妨从这方面入手，设f[i]表示从i到终点的期望，则, 我们要求f[1], 显然终点f[N] = 0， 可以记忆化搜索一下，记忆化实际上就是dp的反向，相当于从终点往前推，即可解出该题。另外一种方式就是建反图，在反图上跑拓扑序进行dp。

记忆化代码：

# include <bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
const int M = 2e5 + 10;
const int INF = 0x3f3f3f3f;
const double INFF = 0x7f7f7f7f7f7f7f7f;
const int mod = 1e9 + 7;
int n, m;
int h[N], e[N], ne[N], idx, w[N];
double f[N];
int dout[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c ,ne[idx] = h[a], h[a] = idx ++;
}double dfs(int u)
{if(f[u] >= 0)return f[u];//期望大于等于0直接返回double res = 0;for(int i = h[u];i != -1;i = ne[i]){int j = e[i];res += (1.0 * w[i] + dfs(j))/ dout[u];}return f[u] = res;
}signed main()
{cin >> n >> m;memset(h, -1, sizeof h);while(m --){int a, b, c;cin >> a >> b >> c;add(a, b, c);dout[a] ++;//表示出边有多少}memset(f, -1, sizeof(f));//初始化一下，表示刚开始都不合法printf("%.2f", dfs(1));return 0;
}

218. 扑克牌

题意：

Admin 生日那天，Rainbow 来找 Admin 玩扑克牌。

玩着玩着 Rainbow 觉得太没意思了，于是决定给 Admin 一个考验。

Rainbow 把一副扑克牌(54 张)随机洗开，倒扣着放成一摞。

然后 Admin 从上往下依次翻开每张牌，每翻开一张黑桃、红桃、梅花或者方块，就把它放到对应花色的堆里去。

Rainbow 想问问 Admin，得到 A 张黑桃、B 张红桃、C 张梅花、D 张方块需要翻开的牌的张数的期望值 E是多少？

特殊地，如果翻开的牌是大王或者小王，Admin 将会把它作为某种花色的牌放入对应堆中，使得放入之后 E 的值尽可能小。

由于 Admin 和 Rainbow 还在玩扑克，所以这个程序就交给你来写了。

分析：
考虑dp，观察发现每个状态都有黑桃数量红桃数量梅花方块数量，和大小王的状态，不妨以此定义状态f[a][b][c][d][x][y], 表示目前卡片数量和大小王状态（0 1 2 3 4）4表示还没翻到. 

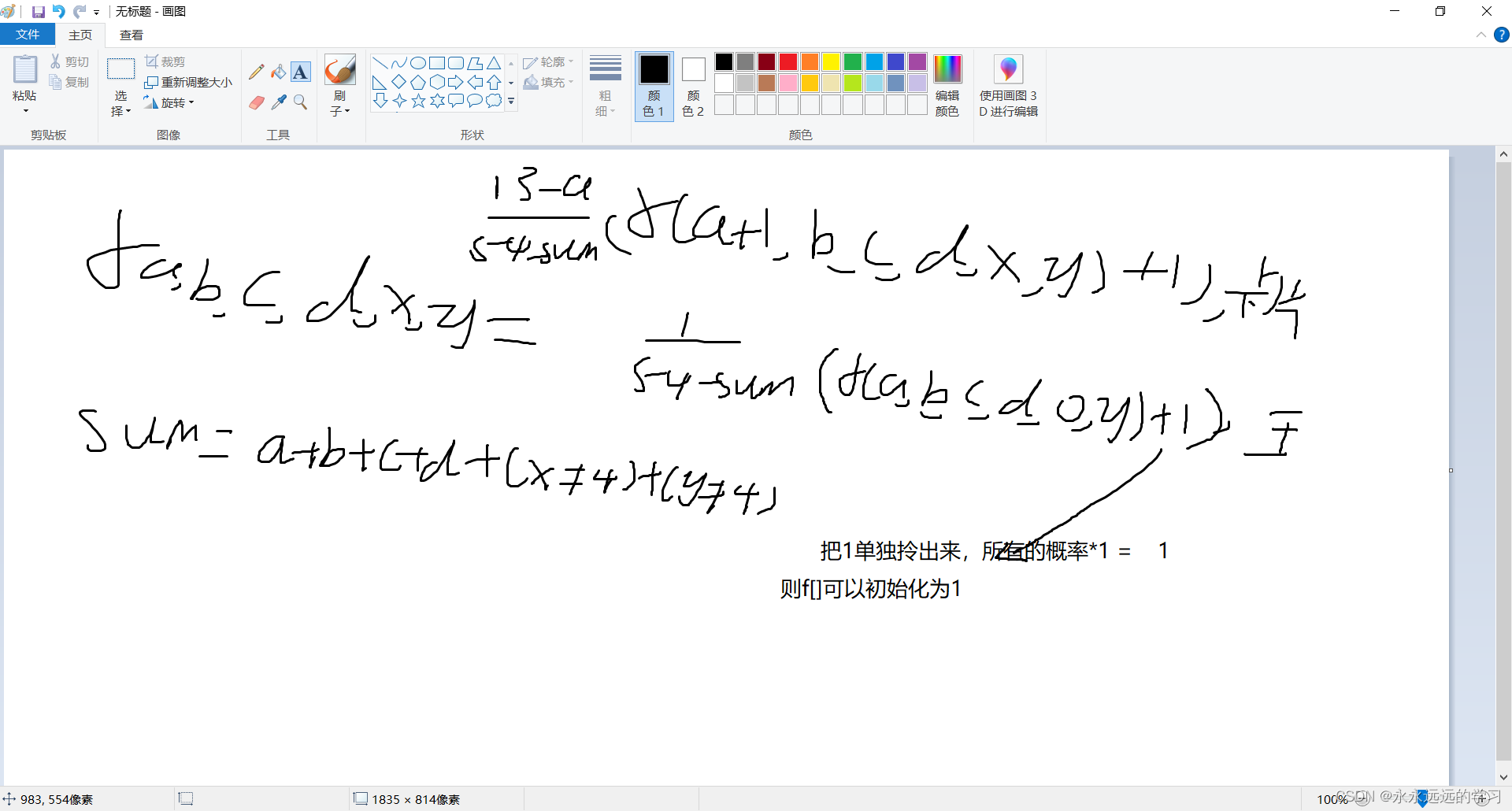代码：
 

# include <bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int N = 20;
const int M = 2e5 + 10;
const int INF = 0x3f3f3f3f;
const double INFF = 1e20;
const int mod = 1e9 + 7;
int A, B, C, D;
double f[N][N][N][N][5][5];double dfs(int a, int b, int c, int d, int x, int y)
{double & v =  f[a][b][c][d][x][y];if(v >= 0)return v;double res = 1;int as = a + (x == 0) + (y == 0), bs = b +(x == 1) + (y == 1);int cs = c + (x == 2) + (y == 2), ds = d + (x == 3) + (y == 3);int sum = a + b + c + d + (x != 4) + (y != 4);if(as >=A&&bs>=B&&cs>=C&&ds>=D)return v = 0;if(sum >= 54){return v = INFF;}if(a < 13){res += (13.0 - a)/(54-sum)*dfs(a + 1, b, c, d, x, y);}if(b < 13){res += (13.0 - b)/(54-sum)*dfs(a, b+1, c, d, x, y);}if(c < 13){res += (13.0 - c)/(54-sum)*dfs(a, b, c+1, d, x, y);}if(d < 13){res += (13.0 - d)/(54-sum)*dfs(a, b, c, d+1, x, y);}if(x == 4){res += min({1.0/(54-sum)*dfs(a, b, c, d, 0, y), 1.0/(54-sum)*dfs(a,b,c,d,1,y),1.0/(54-sum)*dfs(a,b,c,d,2,y),1.0/(54-sum)*dfs(a,b,c,d,3,y)});}if(y == 4){res += min({1.0/(54-sum)*dfs(a, b, c, d, x, 0), 1.0/(54-sum)*dfs(a,b,c,d,x,1),1.0/(54-sum)*dfs(a,b,c,d,x,2),1.0/(54-sum)*dfs(a,b,c,d,x,3)});}return v = res;
}signed main()
{cin >> A >> B >> C >> D;    memset(f, -1,sizeof(f));double ans = dfs(0, 0, 0, 0, 4, 4);if(ans > INFF/2)ans = -1;printf("%.3f", ans);return 0;
}