【精选】算法设计与分析（第四章蛮力法）

本文主要是介绍【精选】算法设计与分析（第四章蛮力法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

第四章蛮力法

1、蛮力法概念

2、蛮力法的优缺点

3、蛮力法设计算法分为两类

4、BF算法——字符串匹配

5、求a的最大连续子序列和

6、简要比较蛮力法和分治法

7、采用蛮力法求解时在什么情况下使用递归

结语

前言

总结算法设计与分析课程期末必记知识点。

第四章蛮力法

1、蛮力法概念

蛮力法基本思路是对问题的所有可能状态一一测试，直到找到解或将全部可能状态都测试为止。

2、蛮力法的优缺点

优点

逻辑清晰，编写程序简洁。
可以用来解决广域领域的问题。
对于一些重要的问题，它可以产生一些合理的算法。
可以解决一些小规模的问题。
可以作为其他高效算法的衡量标准。

缺点

效率不高。
不适用于大规模问题。

3、蛮力法设计算法分为两类

一类是采用基本穷举思路，另一类是在穷举中应用递归。

4、BF算法——字符串匹配

int BF(string s, string t)	//字符串匹配
{int i = 0, j = 0;while (i < s.length() && j < t.length()){if (s[i] == t[j])		//比较的两个字符相同时{i++;j++;}else                    //比较的两个字符不相同时{i = i - j + 1;		//i回退到原来i的下一个位置j = 0;				//j从0开始}}if (j == t.length())			//t的字符比较完毕return i - j;				//t是s的子串，返回位置elsereturn -1;					//返回-1
}

5、求a的最大连续子序列和

#include<stdio.h>
int maxSubSum3(int a[], int n)	//求a的最大连续子序列和
{int i, maxSum = 0, thisSum = 0;for (i = 0; i < n; i++){thisSum += a[i];if (thisSum < 0)			//若当前子序列和为负数，则重新开始下一个子序列thisSum = 0;if (maxSum < thisSum)		//比较求最大连续子序列和maxSum = thisSum;}return maxSum;
}

用蛮力法求解幂集问题的时间复杂度为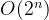 $O(2^n)$

用蛮力法求解全排列的时间复杂度为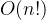 $O(n!)$

6、简要比较蛮力法和分治法

蛮力法是一种简单直接地解决问题的方法，适用范围广，是能解决几乎所有问题的一般性方法。
常用于一些非常基本、但又十分重要的算法(排序、查找、矩阵乘法和字符串匹配等)
蛮力法主要解决一些规模小或价值低的问题，可以作为同样问题的更高效算法的一个标准。
分治法采用分而治之思路，把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题直到问题解决。分治法在求解问题时，通常性能比蛮力法好。