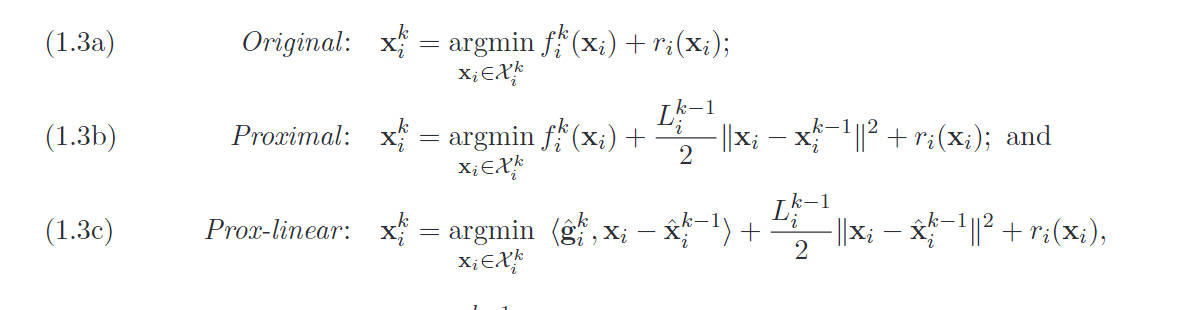本文主要是介绍Zero-Shot Hyperspectral Sharpening:基于Zero-Shot方法的高光谱锐化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Zero-Shot Hyperspectral Sharpening
论文链接:Zero-Shot Hyperspectral Sharpening
代码:
- ZSL_official
- ZSL_format
摘要
近年来CNN在光谱图像融合锐化效果出色,然而这些方法往往缺乏训练数据,泛化能力有限,于是提出了一种用于光谱图象的Zero-Shot学习方法。
具体而言,我们首先提出了一种高精度定量估计成像传感器空间和光谱响应的新方法。在训练过程中,我们根据估计的空间响应对MSI和HSI进行空间抽样,并使用下采样的HSI和MSI来推断原始HSI。这样,我们不仅可以利用HSI和MSI的固有信息,而且训练好的CNN也可以很好地泛化到测试数据中。
此外,我们在HSI上进行了降维,在不牺牲融合精度的情况下减少了模型尺寸和存储使用量。此外,我们为CNN设计了一个基于成像模型的损失函数,进一步提高了CNN的学习性能。
现阶段问题
问题:缺乏训练数据和泛化能力有限
- 图像数据少,难以生成:在实际应用中,难以获取同一场景的LR-HSI,HR-MSI和HR-HSI。为了解决这个训练数据少的问题,在图像去噪领域,Imamura提出对原始噪声图像进行加噪声生成训练数据。但是在全色锐化领域,无法简单通过这种方式进行数据生成。
- 成像模型不同导致CNN泛化性差:当训练数据和测试数据的光谱范围、光谱波段数、成像模型不同时,模型表现会受到影响。为了解决这个问题,Xie通过使用各种常见的成像方式生成训练数据,以尽可能的减小成像不同产生影响。
解决思路:
现阶段生成训练数据,都是假设我们预先知道了光谱响应函数(SRF)和传感器的点扩散函数 (PSF),但是在实际情况中,这两个参数都是难以预先知道的。因此,本文提出一种高精度定量估计光谱和空间响应的新方法。通过从测试数据预先计算SRF和PSF,然后将这两个参数用于生成训练数据,这样就在一定程度保证了训练数据和测试数据在成像模型上保持一致。
主要贡献
- 提出使用HSI锐化的Zero-Shot学习方法,一种高精度定量估计成像传感器空间和光谱响应的方法,用于Zero-Shot学习方法生成数据。
- 对HSI进行降维,提高模型的效率
- 基于子空间表示,设计一个基于成像模型的损失函数,由训练数据损失和成像模型损失组成。
HSI锐化成像模型
常见的将HR-HSI图像变为LR-HSI以及HR-MSI有如下关系,其中B为模糊核(表示空间响应,取决于传感器的点扩散函数 (PSF)),D为下采样因子,R为光谱响应函数(SRF)
X l r = ( X ∗ B ) D + N x , ∗ 为卷积 X_{lr} = (X ∗ B)D + N_x,*为卷积 Xlr=(X∗B)D+Nx,∗为卷积
Y = R X + N y Y = RX + N_y Y=RX+Ny
( Y ∗ B ) D = R X l r + N , \mathbf{(Y*B)D}=\mathbf{RX}_{lr}+\mathbf{N}, (Y∗B)D=RXlr+N,
model-based方法
通过(1),(2),我们可以通过求如下优化问题:
min X ∣ ∣ X l r − ( X ∗ B ) D ∣ ∣ F 2 + ∣ ∣ Y − R X ∣ ∣ F 2 + ϕ ( X ) , \min_\mathbf{X}||\mathbf{X}_{lr}-(\mathbf{X}*\mathbf{B})\mathbf{D}||_F^2+||\mathbf{Y}-\mathbf{R}\mathbf{X}||_F^2+\phi(\mathbf{X}), Xmin∣∣Xlr−(X∗B)D∣∣F2+∣∣Y−RX∣∣F2+ϕ(X),
其中 ϕ ( X ) \phi(X) ϕ(X)表示HR-HSI的先验信息,从上述优化问题我们也知道,必须要提前知道 B B B, R R R才能进行求解,然而 B , R B,R B,R一般都是未知的,只能进行定量估计。
cnn-based方法
通常,基于CNN的方法需要同一场景的LR-HSI,HR-MSI和对应的HR-HSI进行训练,然而这种训练数据是很难获取的,一般都是采用data simulation进行空间和光谱退化生成同一场景的HSI和MSI。
然而,这种方式忽略了模拟中的空间和光谱退化算子应该与测试数据一致,以达到良好性能,这种方法也通常是假设B和R在模拟实验中是完全已知,但在实际中是不成立的,因此,对B,R的定量估计也是只管重要的。
求解过程
由式子1,2,可以得到:
( Y ∗ B ) D = R X l r + N (Y*B)D=RX_{lr}+N (Y∗B)D=RXlr+N
优化问题可以变为:
min B , R ∣ ∣ ( Y ∗ B ) D − R X l r ∣ ∣ \min_{B,R}||(Y*B)D-RX_{lr}|| B,Rmin∣∣(Y∗B)D−RXlr∣∣
由于(6)是非凸的,解不唯一,因此利用先验知识规范化这个优化为题,对就模糊核B进行归一化,并让B,R满足非负约束。
min B , R ∣ ∣ ( Y ∗ B ) D − R X l r ∣ ∣ F 2 s . t . ∑ i , j B i , j = 1 , ∀ i , j , B i , j ≥ 0 , R i , j ≥ 0. \begin{gathered} \min_{\mathbf{B},\mathbf{R}}||(\mathbf{Y}*\mathbf{B})\mathbf{D}-\mathbf{R}\mathbf{X}_{lr}||_F^2\\s.t.\sum_{i,j}\mathbf{B}_{i,j}=1,\forall i,j,\mathbf{B}_{i,j}\geq0,\mathbf{R}_{i,j}\geq0. \end{gathered} B,Rmin∣∣(Y∗B)D−RXlr∣∣F2s.t.i,j∑Bi,j=1,∀i,j,Bi,j≥0,Ri,j≥0.
优化问题相对于B,R是凸的,采用交替最小化方案(alternating minimization scheme)
R ( k ) = argmin R ∣ ∣ H ( k ) − R X l r ∣ ∣ F 2 , s . t . ∀ i , j , R i , j ≥ 0 , \mathbf{R}^{(k)}=\underset{\mathbf{R}}{\text{argmin}}||\mathbf{H}^{(k)}-\mathbf{R}\mathbf{X}_{lr}||_{F}^{2},\:s.t.\:\forall i,j,\mathbf{R}_{i,j}\geq0,\\ R(k)=Rargmin∣∣H(k)−RXlr∣∣F2,s.t.∀i,j,Ri,j≥0,
B ( k ) = argmin B ∥ ( Y ∗ B ) D − E ( k ) ∥ F 2 , s . t . ∑ i , j B i , j = 1 a n d ∀ i , j , B i , j ≥ 0 , \begin{aligned} \mathbf{B}^{(k)}=\underset{\mathbf{B}}{\operatorname*{argmin}}\|&(\mathbf{Y}*\mathbf{B})\mathbf{D}-\mathbf{E}^{(k)}\|_{F}^{2},\\ &s.t.\sum_{i,j}\mathbf{B}_{i,j}=1\mathrm{~and~}\forall i,j,\mathbf{B}_{i,j}\geq0, \end{aligned} B(k)=Bargmin∥(Y∗B)D−E(k)∥F2,s.t.i,j∑Bi,j=1 and ∀i,j,Bi,j≥0,
其中 H k = ( Y ∗ B k − 1 ) D , E k = R k X l r H^{k}=(Y*B^{k-1})D,E^{k}=R^{k}X_{lr} Hk=(Y∗Bk−1)D,Ek=RkXlr

更新R
L ( R , K , L ) = ∣ ∣ H ( k ) − R X l r ∣ ∣ F 2 + μ ∥ R − K + L 2 μ ∥ F 2 + l ( K ) , \begin{aligned}L(\mathbf{R},\mathbf{K},\mathbf{L})&=||\mathbf{H}^{(k)}-\mathbf{R}\mathbf{X}_{lr}||_{F}^{2}\\&+\mu\left\|\mathbf{R}-\mathbf{K}+\frac{\mathbf{L}}{2\mu}\right\|_{F}^{2}+l(\mathbf{K}),\end{aligned} L(R,K,L)=∣∣H(k)−RXlr∣∣F2+μ R−K+2μL F2+l(K),
L L L是拉格朗日算子, l ( ⋅ ) l(\cdot) l(⋅) 是指示函数,当 K K K的所有元素大于0才为0。
l ( K ) = { 0 if ∀ i , j , K i j ≥ 0 , + ∞ otherwise \left.l(\mathbf{K})=\left\{\begin{matrix}0&\text{ if }\forall i,j,\mathbf{K}_{ij}\geq0,\\+\infty&\text{ otherwise}\end{matrix}\right.\right. l(K)={0+∞ if ∀i,j,Kij≥0, otherwise
方程(10)通过交替最小化更新 R , K , L R,K,L R,K,L. R , K R,K R,K根据如下方程更新
R = argmin R L ( R , K , L ) , K = argmin K L ( R , K , L ) \begin{aligned} &\mathbf{R}=\underset{\mathbf{R}}{\operatorname*{argmin}}L(\mathbf{R},\mathbf{K},\mathbf{L}),\\\\&\mathbf{K}=\underset{\mathbf{K}}{\operatorname*{argmin}}L(\mathbf{R},\mathbf{K},\mathbf{L})\end{aligned} R=RargminL(R,K,L),K=KargminL(R,K,L)
(12)的解如下:
R = ( H ( k ) X l r T + μ K − L 2 μ ) ( X l r X l T + μ I ) − 1 K = ( R + L 2 μ ) + R= \left ( \mathrm{H} ^{(k)} \mathbf{X} _{lr}^{T}+ \mu\mathbf{K} - \frac {\mathbf{L} }{2\mu}\right ) ( \mathbf{X} _{lr}\mathbf{X} _{l}^{T}+ \mu\mathbf{I} ) ^{- 1}\\ K=(R+\frac{\mathbf{L}}{2\mu})_+ R=(H(k)XlrT+μK−2μL)(XlrXlT+μI)−1K=(R+2μL)+
( ⋅ ) + (\cdot)_+ (⋅)+是将K的非0元素置0, I I I为单位矩阵
拉格朗日算子 L L L通过如下方式更新
L = L + 2 μ ( R − K ) \mathbf{L}=\mathbf{L}+2\mu(\mathbf{R}-\mathbf{K}) L=L+2μ(R−K)
更新B
( Y ∗ B ) D (Y * B)D (Y∗B)D表示模糊核B和步长的图像Y各波段的二维卷积,因此可以先将 Y Y Y进行分解,并使用stride为s进行下采样,优化问题变为:
min b ∑ i , j ∣ ∣ y i j T b − E i j ( k ) ∣ ∣ F 2 , s . t . ∑ i b i = 1 a n d ∀ i , b i ≥ 0 \operatorname*{min}_{\mathbf{b}}\sum_{i,j}||\mathbf{y}_{ij}^{T}\mathbf{b}-\mathbf{E}_{ij}^{(k)}||_{F}^{2},~~~~~s.t.\sum_{i}\mathbf{b}_{i}=1~~\mathrm{and}~\forall ~i,~~\mathbf{b}_{i}\geq0 bmini,j∑∣∣yijTb−Eij(k)∣∣F2, s.t.i∑bi=1 and ∀ i, bi≥0
令 v = b v=b v=b,同时引入了拉格朗日算子g
E ( b , v , g ) = ∑ i , j ∣ ∣ y i j T b − E i j ( k ) ∣ ∣ F 2 + μ ∣ ∣ b − v + g 2 μ ∣ ∣ F 2 + h ( v ) \begin{aligned} E(\mathbf{b},\mathbf{v},\mathbf{g})&=\sum_{i,j}||\mathbf{y}_{ij}^T\mathbf{b}-\mathbf{E}_{ij}^{(k)}||_F^2\\ &+\mu||\mathbf{b}-\mathbf{v}+\frac{\mathbf{g}}{2\mu}||_F^2+h(\mathbf{v}) \end{aligned} E(b,v,g)=i,j∑∣∣yijTb−Eij(k)∣∣F2+μ∣∣b−v+2μg∣∣F2+h(v)
指示函数如下:
h ( v ) = { 0 if ∀ i , v i ≥ 0 and ∑ i v i = 1 + ∞ otherwise \left.h(\mathbf{v})=\left\{\begin{matrix}0&\text{ if }\forall i,\mathbf{v}_i\geq0\text{ and }\sum_i\mathbf{v}_i=1\\+\infty&\text{ otherwise}\end{matrix}\right.\right. h(v)={0+∞ if ∀i,vi≥0 and ∑ivi=1 otherwise
b = arg min b E ( b , v , g ) = ( ∑ i , j y i j y i j T + μ I ) − 1 ( ∑ i , j E i j ( k ) y i j + μ v − g 2 ) b= \arg\min_bE\left ( \mathrm{b} , \mathrm{v} , \mathrm{g} \right ) \\ =\left(\sum_{i,j}\mathbf{y}_{ij}\mathbf{y}_{ij}^T+\mu\mathbf{I}\right)^{-1}\left(\sum_{i,j}\mathbf{E}_{ij}^{(k)}\mathbf{y}_{ij}+\mu\mathbf{v}-\frac{\mathbf{g}}{2}\right) b=argbminE(b,v,g)=(i,j∑yijyijT+μI)−1(i,j∑Eij(k)yij+μv−2g)
v = argmin v E ( b , v , g ) = argmin v ∣ ∣ b − v + g 2 μ ∣ ∣ F 2 + h ( v ) , \begin{aligned}\mathbf{v}&=\underset{\mathbf{v}}{\operatorname*{\operatorname{argmin}}}E(\mathbf{b},\mathbf{v},\mathbf{g})\\\\&=\underset{\mathbf{v}}{\operatorname*{\operatorname{argmin}}}\left|\left|\mathbf{b}-\mathbf{v}+\frac{\mathbf{g}}{2\mu}\right|\right|_F^2+h(\mathbf{v}),\end{aligned} v=vargminE(b,v,g)=vargmin b−v+2μg F2+h(v),
问题(19)下通过下述引理更新求解(对v的更新)
[63]为L. Condat, “Fast projection onto the simplex and the 1 ball,” Math. Program., vol. 158, no. 1/2, pp. 575–585, 2016.
拉格朗日算子更新:
g = g + 2 μ ( b − v ) g = g + 2μ(b − v) g=g+2μ(b−v)
迭代收敛判断
∥ B ( k + 1 ) − B ( k ) ∥ F ∥ B ( k ) ∥ F + ∥ R ( k + 1 ) − R ( k ) ∥ F ∥ R ( k ) ∥ F ≤ t o l \frac{\|\mathbf{B}^{(k+1)}-\mathbf{B}^{(k)}\|_F}{\|\mathbf{B}^{(k)}\|_F}+\frac{\|\mathbf{R}^{(k+1)}-\mathbf{R}^{(k)}\|_F}{\|\mathbf{R}^{(k)}\|_F}\leq tol ∥B(k)∥F∥B(k+1)−B(k)∥F+∥R(k)∥F∥R(k+1)−R(k)∥F≤tol
f ( R , B ) = Q ( R , B ) + l ( R ) + h ( B ) Q ( R , B ) = ∣ ∣ ( Y ∗ B ) D − R X l r ∣ ∣ F 2 f(R,B)=Q(R,B)+l(R)+h(B)\\ Q(R,B)=||(Y*B)D-RX_{lr}||_F^2 f(R,B)=Q(R,B)+l(R)+h(B)Q(R,B)=∣∣(Y∗B)D−RXlr∣∣F2
命题 1:
假设方阵 X l r X l r T X_{lr}X_{lr}^T XlrXlrT 和 ∑ i j y i j y i j T \sum_{ij}y_{ij}y_{ij}^T ∑ijyijyijT 具有满秩,并且 ( B ( k ) , R ( k ) ) k ∈ N (B^{(k)}, R^{(k)})_{ k\in \mathbb{N}} (B(k),R(k))k∈N,即由算法 1 生成的序列是有界的。在这种情况下,序列将收敛到函数 f f f 的临界点。
证明:
首先,函数 Q Q Q 是可微的,并且其梯度具有 Lipschitz 连续性(由于 ( B ( k ) , R ( k ) ) k ∈ N (B^{(k)}, R^{(k)})_{ k\in \mathbb{N}} (B(k),R(k))k∈N的有界性)。进一步假设方阵 X l r X l r T X_{lr}X_{lr}^T XlrXlrT和 ∑ i j y i j y i j T \sum_{ij}y_{ij}y_{ij}^T ∑ijyijyijT 具有满秩,这表明函数 Q Q Q 对于 B B B 和 R R R 分别是强凸的。除此之外, l ( R ) l(R) l(R) 和 h ( B ) h(B) h(B) 是凸集的指示函数,而 f : R s S × R m ⟶ R f: \mathbb{R}^ {sS} \times \mathbb{R}^m\longrightarrow \mathbb{R} f:RsS×Rm⟶R 满足 Kurdyka-Łojasiewicz(KL)不等式(详见引用 [64] 的2.2Kurdyka-Lojasiewicz inequality)并且具有下界。
基于这些假设和性质,通过直接应用引用 [64] 中的定理 2.8,可以证明序列收敛性。
在这里,假设Algorithm 1是 [64]中Algorithm 1的实例,使用(1.3a)进行更新。
在实际的 HSI 和 MSI 数据中,方阵 X l r X l r T X_{lr}X_{lr}^T XlrXlrT和 ∑ i j y i j y i j T \sum_{ij}y_{ij}y_{ij}^T ∑ijyijyijT 通常具有满秩,这符合上述假设条件。
(1.3a)
子空间表示降维
HSI具有较高的光谱分辨率和许多光谱波段,显著提高了CNN的计算负担和卷积滤波器的数量。为了减少计算负担和参数,我们建议将HSI分解为低维子空间和系数。
利用光谱波段相似度引起的HSI的低秩结构,可以很好地逼近许多真实的HSIs
X = S A X=SA X=SA
上式具体参见Non-local Meets Global: An Iterative Paradigm for Hyperspectral Image Restoration
因为其低秩结构,采用SVD奇异值分解估计光谱子空间
Y = U Σ V T S = U ( : , 1 : L ) Y=U\Sigma V^T\\ S=U(:,1:L) Y=UΣVTS=U(:,1:L)
子空间是半酉的, S S T = I SS^T=I SST=I
A l r = S T X l r , A d = S T X d , A d = ( A l r ∗ B ) D ^ A_{lr} = S^T X_{lr} ,\\ A_d = S^T X_d,\\ A_d=(A_{lr}*B)\hat{D} Alr=STXlr,Ad=STXd,Ad=(Alr∗B)D^
损失函数
l o s s = l o s s g + λ l o s s m = 1 M ∣ ∣ X l r − S A l r ∣ ∣ 1 + λ P ∣ ∣ ( S A l r ∗ B ) D − X d ∣ ∣ 1 + λ Q ∣ ∣ R S A l r − Y d ∣ ∣ 1 \begin{aligned} loss& =loss_g+\lambda loss_m \\ &=\dfrac{1}{M}||\mathbf{X}_{lr}-\mathbf{S}\mathbf{A}_{lr}||_1+\dfrac{\lambda}{P}||(\mathbf{S}\mathbf{A}_{lr}*\mathbf{B})\mathbf{D}-\mathbf{X}_d||_1 \\ &+\frac{\lambda}{Q}||\mathrm{RSA}_{lr}-\mathrm{Y}_{d}||_{1} \end{aligned} loss=lossg+λlossm=M1∣∣Xlr−SAlr∣∣1+Pλ∣∣(SAlr∗B)D−Xd∣∣1+Qλ∣∣RSAlr−Yd∣∣1
其中
-
l o s s g loss_g lossg为训练数据损失,估计的高分辨率 HSI 和地面实况之间的差异损失。
-
l o s s m loss_m lossm为成像损失,也就是通过计算得到的相应矩阵B,R对图像进行转换时的损失。
训练部分
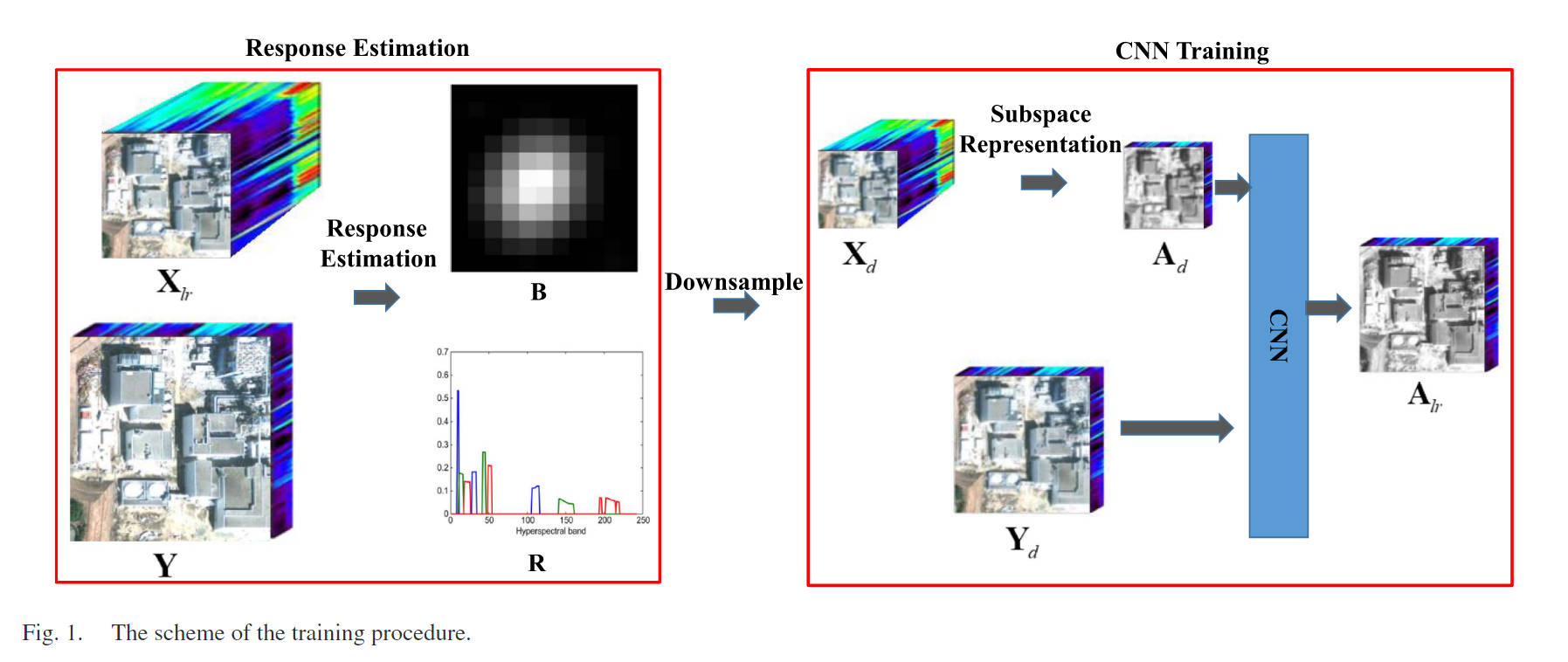
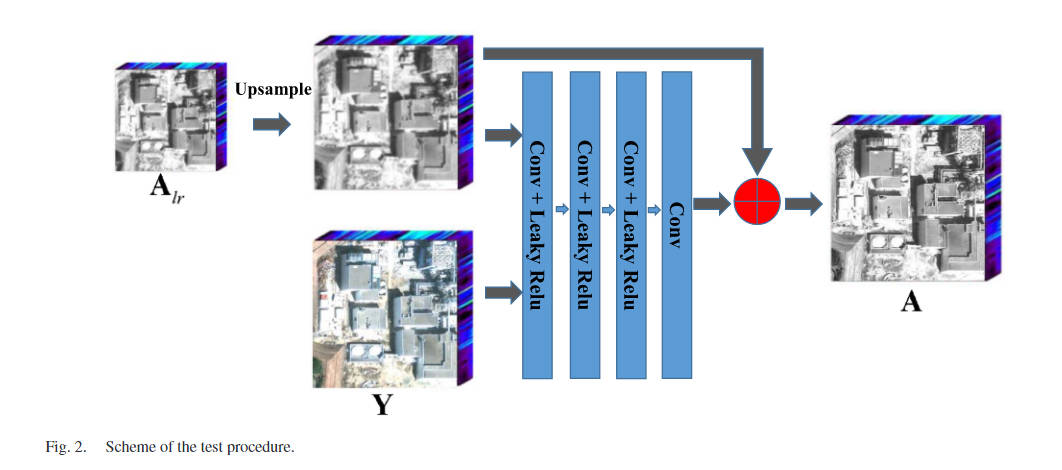
代码:采样 X l r X_{lr} Xlr
[HRHSI, R] = dataset_input(data2, downsample_factor)"""计算X_lr"""
# (X*B)D
HSI0 = Gaussian_downsample(HRHSI, PSF, downsample_factor)
# (X*B)D+N_x=X_lr
HSI0 = HSI0 + 0 * np.random.randn(HSI0.shape[0], HSI0.shape[1], HSI0.shape[2])"""计算y,用来给model提供channel数据"""
MSI0 = np.tensordot(R, HRHSI, axes=([1], [0]))"""子空间表示"""
HSI3 = HSI0.reshape(HSI0.shape[0], -1)
# 奇异值分解用来降维
U0, S, V = np.linalg.svd(np.dot(HSI3, HSI3.T))
# p为论文中的L,该奇异值分解保留了L个最大奇异值
U0 = U0[:, 0:int(p)]
# 论文中的A_lr
HSI0_Abun = np.tensordot(U0.T, HSI0, axes=([1], [0]))上方是针对数据模拟的,假设我们先已知了psf和R,然后从HR-HSI图像先去获取LR-HSI,HR-MSI
如果是实际情况,我们先获取到了HR-MSI和LR-HSI,则只需要以下
"""
模拟数据生成,假设已知psf和R,使用dataset_input
对于真实情况,如果是已知HR-MSI和LR-HSI,可以通过调用Kernal_estimation.m近似求出R和psf
然后将R,psf代入到下面的式子中直接进入子空间表示,降维部分,HSI0=LR-HSI接着对HSI0进行数据增强,然后在生成数据过程中,采样得到X_d,对于Y_d则是通过响应函数直接计算得到。
"""#HSI0=LR-HSI
#MSI:用来提供model初始化输入channel的数据
#psf,R=读取mat得到"""子空间表示,降维"""
HSI3 = HSI0.reshape(HSI0.shape[0], -1)
# 奇异值分解用来降维
U0, S, V = np.linalg.svd(np.dot(HSI3, HSI3.T))
# p为论文中的L,该奇异值分解保留了L个最大奇异值
U0 = U0[:, 0:int(p)]
# 论文中的A_lr
HSI0_Abun = np.tensordot(U0.T, HSI0, axes=([1], [0]))
数据生成
先对 X l r X_{lr} Xlr进行augmentation,此处已经使用降维后的数据代替HSI图像,Abun 表示降维后的。
augument = [0]
HSI_aug = []
HSI_aug.append(HSI0)
U = U0
train_hrhs = []
train_hrms = []
train_lrhs = []
for j in augument:# 垂直翻转HSI = cv2.flip(HSI0, j)HSI_aug.append(HSI)for j in range(len(HSI_aug)):HSI = HSI_aug[j]# MSI = MSI_aug[j]"""计算A_d"""HSI_Abun = np.tensordot(U.T, HSI, axes=([1], [0]))HSI_LR_Abun = Gaussian_downsample(HSI_Abun, PSF, downsample_factor)"""计算Y_d"""MSI_LR = np.tensordot(R, HSI, axes=([1], [0]))"""通过stride移位置遍历图像每一个区域,划分得到training_size尺寸的数值"""for j in range(0, HSI_Abun.shape[1] - training_size + 1, stride):for k in range(0, HSI_Abun.shape[2] - training_size + 1, stride):temp_hrhs = HSI[:, j:j + training_size, k:k + training_size]temp_hrms = MSI_LR[:, j:j + training_size, k:k + training_size]temp_lrhs = HSI_LR_Abun[:, int(j / downsample_factor):int((j + training_size) / downsample_factor), int(k / downsample_factor):int((k + training_size) / downsample_factor)]train_hrhs.append(temp_hrhs)train_hrms.append(temp_hrms)train_lrhs.append(temp_lrhs)#用于当标签
train_hrhs = torch.Tensor(np.array(train_hrhs))
#LR-LSI
train_lrhs = torch.Tensor(np.array(train_lrhs))
#HR-MSI
train_hrms = torch.Tensor(np.array(train_hrms))
matlab代码
demo_kernel_estimation.m:假设已知光谱相应R和通过fspecial求解出初始的psf(B),通过使用R,B对HR-HSI进行转换,得到LR-HSI和HR-MSI。再将LR-HSI和HR-MSI通过kernel_estimation.m进行求解得到R,B
实际应用中,我们一般知道LR-HSI和HR-MSI,然后通过这两个输入到kernel_estimation.m就能求解出相应R,B。然后通过R,B去对图像进行采样操作得到训练数据。
结论
本文介绍了一种新的基于 CNN 的 HSI 锐化方法。与现有方法不同的是,我们的方法基于HSI锐化的成像模型生成训练数据。具体来说,我们首先提出了一种新的方法来准确估计观测到的HSI和MSI的光谱和空间响应。然后,我们利用估计的响应来生成训练数据,可以利用HSI和MSI的固有信息并训练光图像自适应CNN。此外,提出了一种新的损失函数,它由训练数据和成像模型组成,以提高融合性能。此外,我们的方法在CNN的输入和输出中采用降维技术,即可以大大减少CNN的参数,提高计算效率。实验证明,我们的方法可以在不牺牲锐化图像的质量的情况下大大减少计算时间。在未来的工作中,我们还可以考虑利用 CNN 中的估计响应,这可能会进一步提高融合精度。
这篇关于Zero-Shot Hyperspectral Sharpening:基于Zero-Shot方法的高光谱锐化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!