【论文阅读】Reachability Queries on Large Dynamic Graphs: A Total Order Approach

本文主要是介绍【论文阅读】Reachability Queries on Large Dynamic Graphs: A Total Order Approach，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Andy Diwen Zhu, Wenqing Lin, Sibo Wang, and Xiaokui Xiao. 2014. Reachability queries on large dynamic graphs: a total order approach. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data (SIGMOD '14). Association for Computing Machinery, New York, NY, USA, 1323–1334. https://doi.org/10.1145/2588555.2612181

ABSTRACT

可达性查询是图形上的一种基本的查询类型，它可以在许多领域中找到重要的应用程序。尽管已经提出了大量针对可达性查询的技术，但大多数技术都要求输入图是静态的，也就是说，它们不适用于实践中经常遇到的动态图（如社交网络和语义网）。有一些技术可以处理动态图，但没有一种技术可以在不显著损失效率的情况下扩展到规模可观的图。为了解决这一缺陷，本文对大型动态图的可达性指数进行了一种新的研究。我们首先介绍了一个通用的索引框架，它总结了在现有的静态图技术中性能最好的可达性索引家族。然后，我们提出了在该框架下处理顶点插入和删除的通用和有效的算法。此外，我们还展示了我们的更新算法可以用于改进现有的静态图上的可达性技术，并提出了一种在我们的框架下从头开始构建可达性索引的新方法。我们在大量基准数据集上实验评估我们的解决方案，并证明我们的解决方案不仅支持动态图的有效更新，而且提供了比最先进的静态图技术更好的查询性能。

1. INTRODUCTION

给定一个有向图G和G中的两个顶点s和t，可达性查询问是否存在一个路径从s到t。可达性查询是一个基本操作图和有许多重要的应用程序，如查询处理在社交网络，语义Web，XML文档，道路网络和程序工作流程。设计可达性查询索引结构并不简单，因为它需要在预计算成本、索引大小和查询处理开销之间进行仔细的平衡。特别是，如果我们预先计算并存储所有顶点对的可达性结果，那么我们可以在O (1)时间内处理任何可达性查询，但预处理和空间的成本过高。另一方面，如果我们使用深度优先搜索（DFS）或宽度优先搜索（BFS）直接忽略了G上的索引和处理可达性查询，那么我们将最小化空间和预计算开销，但不能确保在大型图上的查询效率。
之前的工作[3-14、16、19、22-25、27-32]已经提出了许多索引技术，以有效地支持可达性查询，而不需要显著的空间和预计算开销。然而，大多数技术都假设输入图G是静态的，这使得它们不适用于实践中经常遇到的动态图。例如，Twitter的社交图谱不断变化，每天增加成千上万的新用户；语义网经常更新新的概念和关系；即使是道路网络也会因为道路封闭和建设而发生变化。有一些技术是为动态图设计的，但是正如我们在第3节和第8节中讨论的，这些技术都不能在不显著效率损失的情况下扩展到相当大的图。具体来说，[4,12,13,16,22,24]中的方法对具有超过100万个顶点的图产生了高昂的预处理成本。同时，[32]中的方法可以处理百万顶点图，但它提供的查询性能通常并不比简单的BFS方法好多少，正如我们的实验所示。
总之，目前没有一种方法能够有效地处理大型动态图上的可达性查询。在此基础上，我们提出了一个关于支持更新的可伸缩可达性指数的全面研究。我们首先介绍了一个总顺序标记（TOL）框架，它总结了用于在静态图上的可达性查询的三种最先进的方法[8,17,30]。TOL有两个重要的属性：(i)TOL下的每个可达性索引都唯一地对应于输入图中顶点的总顺序；（ii）总顺序仅决定了索引在预处理、空间和查询方面的性能。鉴于这些属性，我们研究的算法使我们能够在TOL索引中插入或删除一个顶点，而不改变其他顶点的顺序，也就是说，不会显著降低索引的性能。这就导致了处理TOL下索引上的插入和删除的一般算法。特别地，我们的插入算法是最优的，因为它导致插入后的索引大小最小。有趣的是，我们观察到，我们的更新算法可以通过调整与索引相关的总顺序，来降低TOL索引的空间消耗和查询成本。这就导致了一种改进TOL下的任何指数的一般方法，最先进的技术[8,17,30]。我们的调整方法的有效性表明，[8,17,30]中技术的总阶数留出了很大的增强空间，这促使我们设计新的方法来推导改进的TOL指数的总阶数。因此，我们提出了一个新的可达性索引，蝴蝶，它提供了比TOL [8,17,30]下的任何现有索引都更低的预处理、空间和查询成本。我们使用具有多达2000万个顶点的大量基准数据集来实验评估TOL，并证明了TOL对静态和动态图的替代解决方案的优越性。
综上所述，本文的贡献如下：
我们提出了通用和有效的算法，使TOL框架下的任何索引都能够支持大型动态图（第5节）。
我们开发了一种技术，可以对最先进的可达性指标[8,17,30]进行后处理，以显著提高它们在空间开销和查询效率方面的性能（第6节）。
我们设计了算法来推导TOL下改进的顶点排序，在此基础上我们提出了蝴蝶，一种新的可达性指数，它主导了目前的状态（第7节）。
我们在一组真实图和合成图上评估我们的解决方案，并证明我们的解决方案不仅支持对大型动态图的有效更新，而且提供了比静态图技术更好的查询性能（第8节）。

2. PRELIMINARIES

设G =（V，E）是一个有向图，有一组顶点和一组边。对于V中的任意两个顶点s和t，我们说s可以到达t（记为→），如果G中存在有一条从s开始到t结束的有向路径。给定s和t，可达性查询如果s→t返回TRUE，否则返回FALSE。我们将s和t分别称为查询的源顶点和终端顶点。
如果s→t和t→都成立，那么s和t是强连通的。因此，G的强连通分量（SCC）被定义为V的最大子集，其中任意两个顶点都是强连通的。观察一个顶点u可以到达另一个顶点v，如果以下条件之一成立： (i) u和v属于同一个SCC，或者（ii）有一个路径从包含u的SCC开始到包含v的SCC。鉴于这一观察结果，有一种简单的方法可以将G简化为一个更小的图G∗，以提高可达性查询的效率：
1.计算G.的所有SCCs(这可以在O（|V | + |E|）时间[26]内完成。
2.将每个SCC C映射到一个顶点f ©.对于任意两个SCCs C和C‘，，如果G包含一条边，从C的一个顶点开始，到C’，的一个顶点结束，那么构造一条从f ©到f的有向边（C‘）。将结果图表示为G∗。
3.给定G上从s到t的可达性查询，我们首先检索SSC S。包含s的G的T)。t).然后，当且仅当(i) S和T相同或（ii）f (S)可以达到f (T)时，我们为查询返回TRUE。
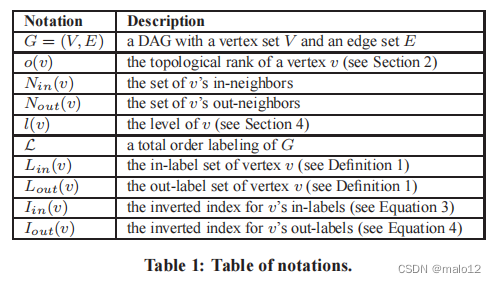
在本文的其余部分中，我们假设G已经用上述的约简方法进行了预处理，即G不包含任何具有多个顶点的强连通分量。（在现有的工作中也做出了同样的假设。）在这个假设下，G应该是一个有向无环图（DAG）。此外，还有：在v上存在一个总阶o，这样对于G中的任意两个顶点u和v，如果u→v，那么o(u)<o(v)（但不一定反之亦然）。这样的总阶数可以在G [8]上的线性时间内使用DFS推导出。我们将o称为拓扑序，将o (u)称为u的拓扑秩。为了便于参考，表1列出了本文中将经常使用的符号。

3. RELATED WORK

现有的关于可达性查询的工作大致可以分为三类（基于它们的查询处理方案）：修剪深度优先搜索、传递闭包检索和双跳标签匹配。下面，我们介绍静态图的技术，然后讨论动态图上的现有方法。
修剪深度优先搜索。这类技术[6,27,31]使用G上的DFS对每个恢复查询进行处理，但它们预先计算G上的某些辅助信息，以修剪DFS的搜索空间，有助于提高查询效率。这类算法中最先进的算法是GRAIL [31]。它通过给每个顶点分配一个区间来对G进行预处理，这样，对于任何两个顶点u和v，如果u的区间不完全包含v的区间，那么uv必须成立。给定这样的间隔，GRAIL使用来自源顶点的DFS回答任何可达性查询，并且它避免访问任何间隔不覆盖终端顶点间隔的顶点。GRAIL的预处理和空间开销很小，但它的查询效率通常比其他两类方法中的方法要差得多。
瞬态闭合检索。顶点的传递关闭u被定义为所有顶点的集合，你可以达到g.方法基于传递闭包检索[3,7,8,10,14,19,25,28,29]预先计算和压缩每个顶点的传递闭包g.给定任何可达性查询，他们首先检索的传递闭包源顶点，将它解压，然后检查终端顶点是否包含在传递关闭。这种方法对于查询处理通常是有效的，但由于在推导和存储传递闭包时存在大量的预计算和空间开销，它们不能扩展到大型图。
2-Hop标签匹配。这类技术[5,8-11,23,30]预处理G，通过为每个顶点v构造两组标签，即外标签集Lout (v)和标签内集Lin (v)。具体来说，Lout (v)中的每个标签都是G中一个v可以到达的顶点，而Lin (v)包含了G中一个可以到达v的顶点的子集。标签集的创建方式是这样的，对于任意两个顶点→和→，我们有s→t当且仅当Lout(t)∩Lin(t)=∅。换句话说，任何可达性查询都可以通过简单地取源顶点的外标签集和终端顶点的标签内集的交集来回答。当标签集很小时，这将导致较高的查询效率。
Cohen等人[11]提出了关于2跳标记技术的第一个研究。他们证明了使标签集的总大小最小化通常是np困难的，并提出了一个（log|V|）近似解。然而，近似解需要O（|V|·|E|log（|V|2/|E|））的预处理时间，这使得它不适用于相当大的图。基于此，许多启发式技术[2、5、8-10、15、18、23、30]被提出，以提高2跳标记的实际效率，尽管抛弃了Cohen等人的方法的近似保证)。在这些技术中，最先进的是TF-Label [8]、分布标记（DL）[17]和修剪地标标记（PLL）[30]，因为它们比其他现有方法（包括基于修剪DFS或传递闭合检索的方法）提供更好的整体性能。在第4节中，我们将介绍一个总结TF-Label、DL和PLL的框架。
动态图形的方法。虽然上述技术都集中在静态图上，但也有一些关于动态图的可达性指数的研究[4,12,13,16,21,22,24]。特别是，[12,13,21,22]提出了在动态图上逐步维护传递闭包的算法。然而，这些算法不能扩展到具有超过几千个顶点的图，如克罗姆米迪亚斯等人的[20]所示。还有两种方法[4,24]扩展了Cohen等人。他的2跳标记方法[11]来处理更新。然而，[24]中的方法仅限于XML图，而[4]无法处理我们实验中使用的百万节点图中的任何一个。此外，[16]提出了一种对可达性索引进行更新的算法，但该索引本身在大型图上产生了巨大的预处理成本。最近，伊尔迪林等人提出了Dagger [32]，这是一个支持动态图的GRAIL [31]的扩展。然而，正如我们在第8节中所展示的，Dagger的查询性能比本文中的解决方案差107倍，而且通常并不比简单的BFS方法好不了多少。

4. TOTAL ORDER LABELING

本节介绍了总顺序标记（TOL），这是一个可达性索引框架，可以实例化到各种2跳标记索引中。TOL的实例化需要两个输入参数，即DAG G =（V，E）和严格的总阶l。我们把l称为水平序。对于任何顶点v，我们将l (v)∈[1，|V |]定义为v在l中的秩，并将l (v)称为v的水平。此外，我们说v有一个更高的值。如果l(v)<l(u)(对应。l (v) > l (u)).
TOL索引的定义。给定G和l，TOL在G上唯一地定义了一个2跳标记索引L，如下：定义1（总顺序标记L）。给定一个DAG G =（V，E）和一个水平阶l，一个TOL索引L是一个2跳标记索引，其中每个顶点与一个标签内集Lin (v)和一个外标签集Lout (v)相关联，这样Lin (v) (resp。Lout (v))包含满足以下所有约束条件的每个顶点u：
可达性约束：u→v(回复。v → u);
等级约束：l (u) < l (v)；
路径约束：从u到v没有一个简单的路径。从v到u)包含一个顶点w与l (w) < l (u)。
我们用下面的例子来说明定义1。
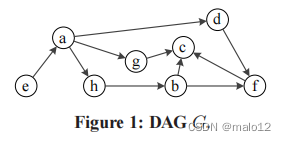
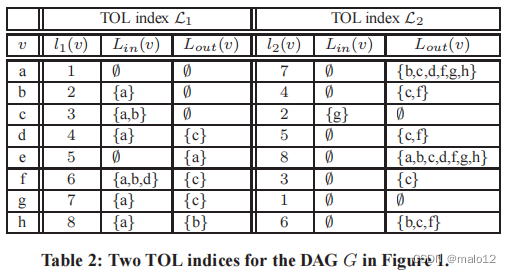
示例1。给定图1所示的DAG G，表2显示了G上的两个指数（即l1和L2）的TOL指数，水平阶分别为l1和l2。考虑G中的顶点g。它在L1中的标签内集合包含a，因为(i) a可以达到g，（ii）a具有高于g的级别，并且（iii）G只包含从a到g的一条简单路径，并且该路径不包含任何级别高于a的顶点。此外，g的标签内集不包含除a以外的任何顶点，因为从任何其他顶点到g的路径必须通过a，而a在l1中具有最小的级别，即，将任何其他顶点添加到Lin (g)违反了定义1中的路径约束。
相比之下，L2中g的标签内设置是∅。这是因为g在l2中具有最小的级别，因此我们不能在不违反定义1中的级别约束的情况下，将任何顶点添加到g的标签内集中。一般来说，由于l1和l2之间的差异，l1的标签集与l2的标签集有很大的不同。
如示例1所示，用于实例化TOL的水平阶l对所得到的可达性指数有深远的影响。因此，如果我们要获得一个高效的TOL指数，我们就必须选择一个适当的水平阶l。在第5节和第7节中，我们将讨论如何为动态图导出和逐步保持良好的级别顺序。为方便起见，我们将TOL索引L的大小定义为L中标签集的总大小，即：



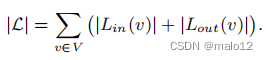
查询算法。给定一个从一个顶点s到另一个顶点t的可达性查询，一个TOL索引L就会像处理其他2跳标记方法一样处理该查询。特别地，L首先检索s的外标签集和t的标签内集，然后按如下方法计算一个见证集：

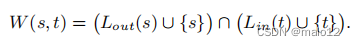
如果见证集为空，则L为查询返回FALSE；否则，L返回TRUE。下面的引理显示了上述查询处理方法的正确性。
引理1。给定任意两个顶点s和t，在s→t中有W（s，t）=∅。
证明。我们首先证明了W（s，t）=∅意味着s→t。注意，当W（s，t）=∅时，至少有以下三种情况中的一种必须成立： (i) t∈Lout (s)、（ii）s∈Lin (t)和（iii）Lin (t)∩Lout (s) =∅。根据定义1，∈Lout (s)和∈Lin (t)都表示。同时，如果Lout(s)∩Lin(t)=∅，然后对于任何∈（Lout）∩Lin (t)，我们有→和→，这导致→。
接下来，我们证明如果→，那么W（→，→）=∅。考虑g中从s到t的所有简单路径的集合。设v是这些路径上所有顶点中级别最高的顶点。我们区分了三种情况： (i) v = t，（ii）v = s，和（iii）v = s和v = t。如果v = t，那么根据定义1，我们有t∈（∈），在这种情况下W（∈，t）包含t，即W（∈，t）=∅。同时，如果v=，那么s∈Lin (t)成立，则得到W（s，t）⊇{s} =∅。最后，如果v=和v = t，那么=必须同时出现在Lout (s)和Lin (t)中，在这种情况下，W（s，t）⊇{v} =∅。
有趣的是，任何TOL索引L中的标签集都是最小的，因为在不影响TOL查询处理算法的正确性的情况下，不能删除任何标签：
引理2。设L是G上的TOL索引，其级别排序为L。对于任何一个顶点u，如果我们从Lout (u)中移除一个顶点v1，那么W（u，v1）=∅but u→v1。同时，如果我们从Lin (u)中移除一个顶点v2，那么W（v2，u）=∅，但是v2→u。
证明。考虑顶点v1。给定v1∈Lout (u)，我们通过定义1有u→v1和l (u) > l（v1）。由于l (u) > l（v1），我们在定义1中的水平约束下有u/∈Lin（v1）。
相反，假设在v1从Lout (u)中移除后，W（u，v1）=∅。然后，根据方程1和u/∈Lin（v1），必须存在一个顶点w∈Lout (u)∩Lin（v1）。在这种情况下，G必须包含一个从u到w到v1的简单路径，并且w必须有一个比u和v1都更高的级别。这与定义1中的路径约束相矛盾，因为v1∈Lout (u)最初成立。顶点v2的情况也可以用类似的方式来建立。
TOL的现有安装程序。根据定义1，TOL定义了一系列满足可达性、级别和路径约束的2跳标记方法。这个索引家族不包括所有现有的2跳标记方法（因为它们中的许多违反了上述的约束条件），但它捕获了三种最先进的2跳标记技术，即TF-Label [8]、DL [17]和PLL [30]。特别地，TF-Label利用了G中顶点的拓扑顺序o（o的定义见第2节）。它以这样的方式构建索引：(i)一个顶点v的标签集只包含具有o (v) < o (u)的顶点u，并且（ii）标签集是最小的。它可以显示TF-Label对应于一个TOL索引，该TOL索引使用o作为级别顺序（当多个顶点在o中具有相同的秩时，将任意打破绑定）。
同时，DL将G中的顶点按度的降序排序，并按照排序的顺序检查G中的顶点，并相应地构造标签集。具体来说，每次它检查一个顶点v时，它都使用G上的两个受约束的BFSs来识别一些(i)连接到v和（ii）按排序顺序排名低于v的顶点；然后，它将v添加到这些顶点的标签集中。可以证明DL等价于一个TOL索引，其中层序将顶点按其度的降序排列。最后，由于PPL与DL [17]等价，它也是TOL的一个实例。
值得注意的是，如果我们修改DL中的顶点顺序，并使用修改后的顺序基于DL的预处理算法构造可达性索引，那么得到的索引等效于采用相同修改顺序的TOL索引。换句话说，任何TOL索引都可以使用DL的预计算算法的修改版本来获得。然而，描述DL [17]的论文并没有总结出支撑TOL的可达性、级别和路径约束（见定义1）。在我们的论文中，对这些约束条件的总结是至关重要的，因为它们在我们分析如何逐步更新TOL指数时是非常必要的（见第5节）。

5. INCREMENTAL UPDATES

在本节中，我们将研究当一个顶点被插入或从g中删除时，TOL索引L如何被增量更新。我们的目标是双重的：
1.L在任何更新后都应该保持一个TOL索引，也就是说，它应该始终满足定义1中的约束条件。这是为了保证L的查询算法的正确性和L的标签集的最小性。
2.插入或删除一个顶点不应改变其他顶点上的级别顺序l。直观地说，这减少了L的标签集中所需的更改量，并有助于在更新后保留L的性能，因为TOL索引的标签集（因此，它的性能）完全是由其级别顺序决定的。

5.1 Insertion Algorithm

考虑我们在G中插入一个新的顶点v，并将v与G中一些现有的顶点连接起来。让G=（V，E）是插入后得到的图。根据之前的工作[4,32]，我们假设G也是一个DAG。当G不是一个DAG的情况下，可以通过逐步维护G中的强连接组件来处理，如在[32]中所讨论的。设L是G上的TOL索引，水平阶为L。如前所述，我们的目标是将L更新为G上的L，级别为，，这样对于任意两个顶点u1，u2∈V，l（u1）< l（u2）iff l（u1）<（u2）。
简而言之，我们的插入算法分两个步骤运行：在步骤1中，它决定l(v)的值，然后为G中的任意顶点u设置l(u)如下：

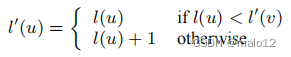
然后，在步骤2中，根据L，更新L中的标签集，将L转换为L.为了便于说明，我们将首先详细说明步骤2，假设l已经构造了。

5.1.1 Step 2: Updating Label Sets

给定G，L和l，，我们的插入算法的第二步进一步分为两个子步骤。在步骤2.1中，我们为新的顶点v创建标签集(v)中的L和Lout(v)，并将v插入到其他顶点的标签集中。然后，在步骤2.2中，我们进一步细化了V中顶点的标签集，从而将L转换为L.在整个算法过程中，对于每个顶点u，我们保持两个反向列表Iin (u)和Iout (u)，这样一来

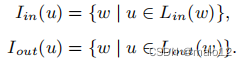
换句话说，如果你出现在标签内(回复。然后w被记录在倒置的列表Iin (u)中。Iout (u)).这些倒置的列表使我们能够有效地识别受任何顶点u影响的标签集。此外，它们可以很容易地维护关于标签集的更改。

步骤2.1。算法1显示了第一步的伪代码。该算法首先创建一个候选集Cin(v)（第1-4行)，然后将其细化为v(（第5-10行）的(v)中的标签内集L。特别地，候选集Cin (v)包含v的所有内邻（即指向v的边的起始顶点），以及这些内邻的标签内集（Line 3-4）。
根据定义1，Cin (v)是L.中v的标签内的超集为了解释，考虑一个顶点u，它是L.中v的标签内根据可达性约束，在G.中存在一个从u到v的路径P设w是冯·p的内邻，那么，你可以到达w。此外，l (u) < l (w)；否则，w是P上一个级别高于u的顶点，这违反了路径约束。最后，从u到w的所有路径应该只包含级别低于u的顶点；否则，u首先不应该是v的标签内。以上这些都表明u是w的标签内，因为它满足了定义1中的三个约束。因此，Cin (v)是L.中v的内标签的超集。
为了将Cin (v)细化为(v)中的L，算法1删除了Cin (v)中违反定义1（第5-10行）中的任何水平和路径约束的顶点。（可达性约束被忽略，因为Cin (v)中的所有顶点都可以达到v）具体地说，算法检查Cin (v)中的顶点按级别值的升序。对于每个具有l(u)<l(v)（即u满足水平约束），如果(v) =∅中的Lout(u)∩L，算法将u添加到(v)中的L中。其原理是，如果在(v) =∅中Lout (u)∩L，那么没有一个高于l (u)的顶点可以连接到v，在这种情况下u填充路径约束。同时，如果Lout在(v) =∅中的Lout (u)∩L，但是l(u)>l(v)，那么我们将v添加到u的外标签集Lout (u)中。在创建了(v)中的L后，算法1构造了Lout(v)（第11-13行），然后终止。我们省略了关于Lout(v)的讨论，因为它类似于(v)中的L的情况。

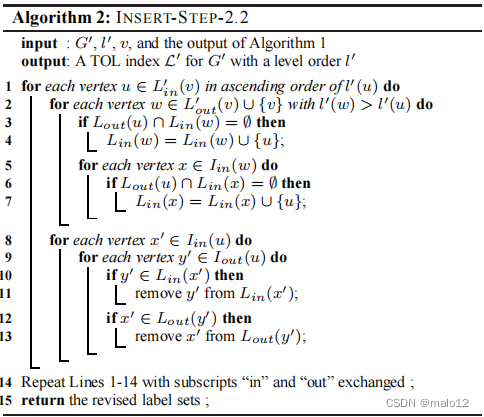
步骤2.2。给定步骤2.1的输出，我们的算法的步骤2.2继续细化L中的标签集，如算法2所示。其基本原理是，由于V的插入在V中的顶点之间创建了新的路径，因此我们可能需要调整L中的标签集，以确保L仍然是一个TOL索引。具体来说，算法2首先检查(v)中的L中的顶点，按其级别值的升序排列（第1行）。对于每个顶点u，该算法检查Lout(v)∪{v)中的每个顶点w，其级别低于u（行2）。注意，对于每一对这样的顶点u和w，v的插入会创建一个从v从u到w的新路径。因此，如果Lout (u)∩Lin (w) =∅，即如果将u插入到Lin (w)中不违反定义1（第3-4行）中的路径约束，则该算法将u添加到w的标签内集Lin (w)中。类似地，该算法还将u插入到Lin (x)中，对于任何顶点x∈Iin (w)，即任何以w作为标签内的顶点x（第5-7行）。
之后，算法继续检查第2-7行中的操作是否产生了不必要的标签（第8-13行）。特别地，它检查每一对顶点x∈Iout (u)和y∈Iin (u)，也就是说，x有u作为外标签，y有u作为内标签。对于每一对x和y，，算法检查y是否出现在x；的外标签中，如果是，它从Lout（x）中删除y，因为(i) u的级别比x和y都高，并且（ii）u连接x到y，，这导致违反路径约束。类似地，如果x在y，的外标签集中，那么它将被删除。
一旦完成上述嵌套循环，算法2进入另一个嵌套循环，其中(i)外环线性扫描每个顶点uL(v)水平值的升序，和（ii）内部循环检查每个顶点wL(v)∪{v}与l(u) < l(w)。这个嵌套循环补充了前一个嵌套循环，因为前一个处理(v)中的L和Lout(v)中的顶点对，后者忽略。最后，算法2终止并返回修正后的标签集，这构成了L.

5.1.2 Step 1: Deciding Vertex Level

我们在第5.1.1节中的算法要求确定新顶点v的水平l(v)。一个简单的方法是设置l(v) = |V | + 1，即给出v个可能的最低级别。这导致了相对较小的更新开销，因为当l(v)最大化时，我们不需要将v插入到任何其他顶点的标签集中（由于定义1中的级别约束）。然而，就空间开销和查询效率而言，设置l(v) = |V | + 1可能比其他选择l(v)非常次优。为了解决这个问题，我们提出了一种替代解决方案，它将l(v)设置为一个尽量减少标签集的总大小的值。这样的l(v)也有可能提高查询效率，因为在TOL索引上的可达性查询的成本与源和终端顶点的标签集的大小是线性的。
设Lk为用l(v) = k将v插入到L中得到的TOL索引。为了识别使L最小化的k的值，我们检查了所有可能的k∈[1，|V |+ 1]，但避免重复使用算法1和算法2来构造所有的L∈。相反，我们提出了一种轻量级的衍生方法

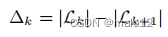
对于任何k∈[1，|V |]。一旦计算出了Δk，我们就可以很容易地确定l(v)的最优值。
我们的方法背后的关键观察结果如下。当我们将l(v)从k更改为k−1时，所有顶点的能级阶保持不变，除了v和l (u) = k−1（因为u和v之间的阶会颠倒）。因此，Lk和Lk−1之间的大小差异只取决于与u和v相关的标签集。直观地说，跟踪这些标签集中的变化比从中创建TOL索引要简单得多因此，推导出Δk可以比构造Lk更有效。
算法3显示了我们的方法的伪代码。它首先设置l(v) = |V | + 1，并应用算法1计算v的两个标签集L在(v)和Lout(v)和两个反向列表在(v)I和Iout(v)（行1-2）。该算法的后续部分包括|V |迭代（第3-14行）。在（||−k+1）迭代中，算法考虑l(v)从k + 1变为k的情况，并计算标签集中相应的变化，以此推导Δk。
具体来说，算法首先设置Δk = 0，用l (u) = k检查顶点u，即当l(v)从k + 1降低到k时，级别与v交换的顶点。请注意，如果u和v之间的交换导致某些标签集的变化，那么(v)∪Lout(v)中的u∈L应该成立。原因是，当u/∈L在(v)中，(i)u和v之间没有路径，或者（ii）u和v之间的所有路径都包含至少一个水平高于u和v的顶点。在任何一种情况下，在u和v之间切换级别都不会导致违反任何标签集中的可达性、级别或路径约束。因此，如果u/∈L在(v)∪L在(v)中，那么交换u和v的级别将不会影响标签集。基于此分析，每当(v)∪Lout(v)中的u/∈L（第4-13行）时，算法3将Δk的最终值设置为0。
现在考虑一下u∈LL在(v)中的。在我们交换u和v的水平后，u应该从(v)中的L中移除，v应该成为u的外标签。这就解释了算法3中的第7行。同时，对于(v)中的任何顶点w∈I（即，w有v作为标签内），我们检查u是否是w的标签内（第8行）。如果u∈Lin (w)，那么在u和v的水平被交换后，由于路径约束，u应该从Lin (w)中移除，这将Lin (w)的大小减小1。因此，算法3对每个这样的顶点w（第9行）减少Δk 1。此外，对于任何顶点w∈out(u)（即，u是w的外标记），我们检查v是否不是w（第10行）。如果v/∈Lout（w），那么在我们交换u和v的级别后，v将成为w，的外标记，即Lout（w）的大小增加1。因此，对于每个这样的顶点，，算法3将Δk增加1，并将w插入Iout(v)（第11和12行）。可以验证的是，除了上述标签集外，任何其他标签集都不会受到u和v之间的交换的影响。
虽然上面的讨论假设了u在(v)中的∈L，但它可以很容易地扩展到当u∈Lout(v)时的情况（第13行）。Once all Δk are obtained, Algorithm 3 derives |V | + 1 variables θ1, θ2,…,θ|V |+1, such that θ|V |+1 = 0 and θk = θk+1 + Δk (k ∈ [1, |V |]).根据Δk的定义，最小化θk的k值也应该最小化|Lk|。因此，算法3通过返回argmink{θk}（第18行）来终止。

5.1.3 Correctness and Complexity

我们首先在引理3中证明了插入算法的正确性，然后分析了其复杂度。
引理3。给定G和一个新的顶点v，算法1和算法2在G，上产生一个TOL索引，算法3计算出v的一个级别，使其最小化L.的标签大小。
证明。我们首先证明了算法1和算法2产生的指数L是G.上的TOL指数特别地，我们首先展示了算法1和算法2中的第1-7行创建的标签集是G，上TOL中相应标签集的超集，然后展示了算法2中的第8-13行删除了所有冗余标签。
回想一下，我们已经证明了在第5.1.1节中由算法1创建的(v)中的L和Lout(v)的正确性。下面，我们证明了，对于除了v之外的任何顶点u，算法2中的第1-7行创建了一个标签内集，它是G.上TOL中u的标签内集的超集给定两个顶点u和x，根据定义1，v的插入使u成为x的标签内，只有当以下所有条件都成立： (i) l(u)<l(x)；（ii）u可以在G中达到v，v可以在G；（iii）从u到x的简单路径不包含比u高的顶点。因此，在第1行中，我们省略了(v)中不在L中的任何顶点u。这是因为如果u不在(v)中的L中，那么对于从u到v的所有路径中级别最高的顶点z，我们有z = u。此外，z也在从u到v可以到达的任何x的路径上。在这种情况下，条件（iii）被违反，因此，u将永远不会成为G.中任何顶点的标签内。
接下来，考虑由第2行消除的任何顶点x。如果x的级别高于u，那么它应该被消除，因为它违反了条件(i)。另一方面，如果x的水平低于u，那么x就不在Lout(v)∪{v}中。在这种情况下，对于从v到x be z的所有路径中级别最高的顶点z，我们有z∈Lout(v)。如果l(z)>l(u)，那么当w = z时，在循环中检查x。如果l(z)<l(u)，那么有一个从u到x的路径，它包含一个顶点（即z），违反了条件（iii）。此外，第3行和第6行还保证新创建的标签不违反条件（iii）。总之，第1-7行只省略了永远不会导致标签创建的顶点，因此，在第1-7行中创建的标签内集集是G.上TOL中相应的标签内集的超集。
将u添加到Lin (x)后，一些与x相关的现有标签可能会变得多余。根据定义1，现有标签的级别约束和可达性约束都不会受到影响，也就是说，唯一可能的违反是在路径约束。特别是，你可能是一个顶点y的标签，这样y是一个标签的x或x是一个标签的y，这导致违反路径约束因为(i)有一个路径从y到x，和（ii）u水平高于y和x。为了解决这个问题，算法2枚举了第8行和第9行中所有相关的x和y，并删除了第10-13行中的冗余标签。
在此之后，我们重复上面的过程（第14行），交换“in”和“out”，以更新可以到达v的顶点的标签内集，以及v可以到达的顶点的标签外集。总结以上讨论，算法1和算法2在G.上产生了一个TOL
最后，由于算法3精确地评估了v的连续级别之间的大小差异，即Δi，i=1，…，|V|（如第5.1.2节所示），它确定了v的级别k，从而使结果索引的大小最小化。

复杂性分析。为了分析我们的算法，我们一步一步地考虑了复杂度。在步骤1中，给定一个顶点v进行插入，算法3检查(v)∪Lout(v)中的所有顶点u∈L，并通过计算所有顶点w∈∈(u)∪∈(u)得到Δk，每个顶点都有一个集合操作，即第8行和第10行。设β为一个集合操作的代价，则步骤1的复杂度以O（|V | 2β）为界。在步骤2.1中，算法1导致第6行||(v)|+|Cout(v)|集合操作的|数，因此，其成本以C2 = O（（|Cin (v)| + |Cout (v)|）β）为界。在步骤2.2中，算法2在最坏的情况下对每对顶点执行集合操作，导致复杂度为O（|V | 2β）。请注意，第9-14行检查Iin (u)∩Lin（x）和Iout (u)∩Lout（y）中的顶点，这也可以在集合操作中实现。因此，我们的整个插入算法的复杂度是O（|V | 2β）。

5.2 Deletion Algorithm

接下来，我们讨论我们的算法处理删除G.让G=（V，E）图获得从删除一个顶点vG.插入的情况下，我们假设G是一个达，我们的目标是转换LL指数LG，L和L排序的顶点在V以相同的顺序。
算法4给出了我们的删除方法的伪代码。它首先从它出现的每个标签集（第1-第4行）中删除v。然后，它改进了L中的标签集，并将其转换为L（第5-22行）。特别地，它首先检索v可以到达的所有顶点的集合B+(v)，使用一个来自v的BFS，它跟随每个顶点的输出边。然后，对B+(v)中的顶点进行拓扑秩的升序检查（见第2节），并重建每个顶点的标签内集。（请注意，这些顶点的外标签集不受删除v.的影响。）
对于每个顶点u∈B+(v)，算法首先创建一个候选集Cin(u)（第8行）。然后，对于每个u的内邻z，即z = v，算法将z的内标签插入Cin(u)（第9-10行）。可以证明Cin (u)是L.中u的内标签的一个超集为了将Cin (u)细化为u的标签内集，该算法以lin(u)的升序检查Cin (u)中的每个顶点w。如果l (w) < l (u)和Lout (w)∩Lin (u) =∅，那么我们将w识别为L（第14行）中u的标签内。随后，我们删除了由于将w插入到Lin (u)中而变得多余（第15-17行）的标签。特别地，对于每个顶点s都是一个外标签，如果u也在s的外标签集中，那么我们从s的外标签中删除u。
一旦B+(v)中的所有顶点被处理，算法通过应用从v开始的每个顶点的BFS，得到可以到达v的顶点的集合B−(v)。在此之后，它重建了B−(v)中每个顶点的外标签集，其方式类似于B+(v)的情况（第18-21行）。最后，它返回所有期望v的顶点的修改标签集，即形成L.的标签集。
正确性证明。引理4证明了我们的删除算法的正确性。
引理4。给定G和一个要删除的顶点，算法4产生的更新的标记L是G.上的TOL
证明。我们首先证明了在第8-10行中生成的候选集Cin (u)是(u)中的L的一个超集。然后，我们证明了在(u)中的冗余标签在第12-19行的L中被删除。

考虑每个顶点x，它是u的一个更新的标签内（即(u)中的x∈L）。通过定义1中的可达性约束和路径约束，我们知道在G，中有一个从x到u的路径，并且x是该路径上的最高级顶点。设z是路径上u的标签内。然后，x = z或x是z的更新标签内（即，(z)中的x∈L）。为了理解这一点，相反地假设(z)中的x = z和x/∈L。然后，必须有一个从x到z的路径P，它包含一个比x和z都高的顶点。考虑一个路径P，它通过P从x到z，然后从z到u。观察到P连接x到u，并包含一个级别高于x的顶点。这与路径约束相矛盾，因为x∈L在(u)。综上所述，对于(u)中L中的任何顶点x，它要么是u的内邻，要么是u的内邻的标签内邻。因此，第8-10行通过组合u的所有内邻以及这些内邻的内标签来构建候选集Cin (u)。此外，由于我们在(u)中构造L以o (u)的升序构造，我们确保u的内邻集在Cin (u)的标签内构造之前更新，这保证了Cin (u)是(u)中L的超集。
接下来，对于Cin (u)中的每个顶点w，我们将它加入到(u)<(u)和(u)∩Lout (w)∩(u) =∅中的L中。这就保证了对级别和路径的约束。由于可达性约束在候选集的构造中已经得到了保证，所以我们知道在(u)中的L中添加w并不会影响TOL属性。然而，一些与w和u相关的现有标签可能会变得多余。根据定义1，级别约束和可达性约束都不会受到影响，唯一可能的违反是关于路径约束。特别地，如果w也是一个顶点s的外标记，如果u在s的外标记中，那么u违反了路径约束，因为有一个从s到u的路径包含w，并且w的级别比u高于u。另一方面，s是u的一个内标签的情况永远不会发生，因为我们以l (w)的升序在(w)中将w加到L中。
总结上面的讨论，对于每个顶点u，我们首先在(u)中生成一个L的超集，然后通过从超集中添加顶点来构造(u)中的L。此外，对于在(u)中添加到L中的每一个w，我们动态地删除了由w引起的所有冗余标签。因此，算法4在G.上产生了一个TOL。
复杂性分析。计算B+(v)和B−(v)的复杂度相当于G中BFS的复杂度，即O（|E|）。接下来，考虑B+(v)中的一个顶点u的计算代价。在第9-10行中，当我们合并u的内邻的更新的标签内集以形成u的候选集时，复杂度以|V |β为界，其中β是集合操作的复杂度。然后，对于候选集Cin (u)中的每个顶点x，需要恒定数量的集操作将x添加到Lin (u)并删除冗余标签。因此，u上的总计算代价以O（|V |β）为界。因此，删除算法的复杂度为O（|V | 2β）。

6. ITERATIVE LABEL REDUCTION

第5节中的更新算法保留了G中顶点上的级别顺序，如前所述，这有助于确保L的性能在更新后不会显著下降。但是，由于在更新期间保留了初始级别的顺序l，因此必须仔细选择l。否则，如果l使L效率低下，那么这种低效率很可能即使在更新之后也会持续存在。
选择初始l的一个简单的解决方案是枚举所有可能的级别顺序（即V中所有顶点的排列），然后根据每个顺序构造一个TOL索引，最后选择一个优化性能的索引。然而，由于有大量可能的级别订单，这种方法远不实用。作为一种替代解决方案，可以使用一些启发式方法（例如，使用现有的TOL实例[8,17,30]）选择初始阶l，然后调整初始阶l来改进l。有趣的是，我们的更新算法可以用于调整l。
具体来说，给定L，我们可以首先使用算法4移除一个顶点v，然后使用第5.1节中的插入算法将v向回插入。插入算法的属性，当v重新插入时，其水平l (v)设置为一个值最小化|L|，例如，标签集的总大小l因此，|L|可能减少（永远不会增加）后删除和重新插入v。通过对每个顶点v重复这个过程，我们可以得到一个改进版本的L，并且（大大）减少了总大小。|L|的减少不仅减少了空间消耗，而且提高了查询效率（如L通过扫描标签集来处理查询）。在第8节中，我们通过实验表明，这种标签缩减方法可以显著提高现有TOL实例化[8,17,30]的性能。

7. CONSTRUCTION OF INITIAL L

虽然标签约简算法提高了L的性能，但我们从实验中观察到，它在大图上产生了大量的计算成本。这促使我们研究更有效的方法来选择一个好的初始水平阶l。下面，我们首先提出了一个构造初始l的新算法（第7.1节），然后讨论了给定l的l的构造（第7.2节）。

7.1 Deciding Vertex Level

给定一个G和一个顶点v∈，设Sin（∈，G）是在G中可以达到∈的顶点集合，而Sout（∈，G）是v在G中可以达到的顶点集合。假设我们设置v的水平高于Sin（v，G）∪Sout（v，G）中任何顶点的水平。然后，在相应的TOL索引中，我们需要将v添加到Sin（v，G）中的顶点的标签内集，以及Sout（v，G）中的顶点的标签外集。在这种情况下，v在L中贡献了|Sin（v，G）| + |Sout（v，G）|标签。
另一方面，如果我们将v的级别设置为比Sin（v，G）∪Sout（v，G）中的所有顶点更低的级别，那么我们需要(i)将Sin（v，G）中的每个顶点添加到Lin (v)中，以及（ii）将Sout（v，G）中的每个顶点添加到Lout (v)中。此外，如果v恰好是唯一一个将Sin（v，G）中的顶点与Sout（v，G）中的顶点连接起来的顶点，那么在最坏的情况下，我们必须将Sout（v，G）中的每个顶点添加到Sin（v，G）中每个顶点的外标签集中。在这种情况下，v在L中贡献了|Sin（v，G）|·|Sout（v，G）|+|Sin（v，G）|+|Sout（v，G）|标签。
我们将|Sin（v，G）|和|Sout（v，G）|分别定义为v的内分和外分。此外，我们还定义了一个分数函数f，如下所示：

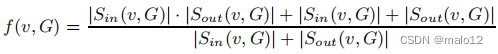
在病理病例中，当|Sin（v，G）| + |Sout（v，G）| = 0时，我们定义了f（v，G）=0。直观地说，如果f(G)很大，那么v应该给出一个更高的顶点罪(G)∪鼻子(G)，以避免最坏情况的空间成本|罪(G)|·|鼻子(G)|+|罪(G)|+|Sout(G)|。
基于以上直觉，我们可以设计一个算法来推导一个好的水平阶l。给定G，我们首先确定使f（v1，G）最大化的顶点v1，然后设置l（v1）=1，即，我们将v1分配到最高水平。在此之后，我们从G中删除v1，并继续识别在修改后的G中使f（v2，G）最大化的顶点v2，然后设置l（v2）=2。我们重复这个过程，直到从G中删除所有的顶点，也就是说，直到每个顶点都给定一个级别。
虽然上面的算法是直观的，很难有效地实现，(i)f（v，G）的计算要求我们获得的得分和得分v使用BFS（或DFS）G，和（ii）一个顶点的得分和得分需要重新计算当另一个顶点从G。解决这个缺陷，我们建议近似的得分和得分的顶点G。
设Sin(v)和Sout(v)分别是一个顶点v的近似得分和得分。对于G中没有内邻居的每个顶点w。外邻)，我们在(w)=0中设置S。Sout(w)=0)到零；注意，这也是确切的输入分数。超过)的w。然后，基于这些顶点w，我们递归计算每个剩余顶点v的近似分数和分数如下：

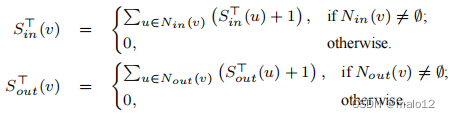
其中，Nin (v)和Nout (v)分别表示v的内邻和外邻的集合。可以验证(v)中的S和Sout(v)分别是v的得分和分的上界。作为一种替代解决方案，我们还考虑使用v的分数的下限。，在(v)中表示为S⊥。S⊥out (v))，用于近似。特别是，如果v没有内邻，则⊥在(v)=0，如果v没有外邻，则⊥out (v)=0。对于任何其他的顶点，我们都有：


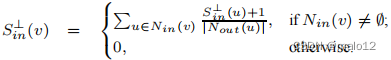
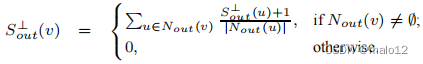
注意，我们可以为G中所有顶点v的线性扫描计算(v)中的S，使用顶点的线性扫描。具体地说，我们按照其拓扑秩o (v)的升序检查顶点v（见第2节）。由于G是一个DAG，排名最小的顶点必须没有内邻，因此，对于这些顶点中的任何一个，我们在(u)=0中都有S。根据拓扑秩的定义，当我们检查任何其他顶点w时，必须计算出w的内邻值中的S。因此，在(w)中的S可以很容易地推导出来。综上所述，我们可以计算O（|V |+|E|）时间内所有顶点v的(v)中的S。同样的算法可以很容易地扩展到(v)中的S⊥。同时，我们可以利用G中的顶点按降序对Sout (v)和所有顶点v的Sout (v)和S⊥out (v)进行线性扫描。

7.2 Labeling Algorithm

如第4节中所讨论的，级别阶l唯一地决定TOL索引l。在本节中，我们介绍一种构造给定使用7.1节中的方法计算的级别阶l的算法。在[2,17]中也对TOL的特定实例化（具有特定级别的排序）提出了类似的方法，但其中的正确性分析并不立即适用于一般的TOL框架。因此，为了完整性，我们提出了我们的算法和分析。
算法算法5给出了我们的方法(称为蝴蝶构造L，给定L的级别为l。算法首先创建一个G的副本（称为G1），然后在|V |迭代中运行。在第k次迭代中，它从Gk中删除带有l (v) = k的顶点v，并将v插入到其他顶点的标签集中。特别地，我们首先得到Gk中v可以到达的顶点的集合B+(v)，使用v中跟随每个顶点的出边的BFS。然后，对于每个顶点w∈B+(v)，如果Lout (v)∩Lin (w) =∅，那么我们将v加到Lin (w)中。在此之后，我们根据每个顶点的输入边从v开始对Gk执行一个BFS，以识别在Gk中可以达到v的顶点的集合B−(v)。对于每个u∈B−(v)，我们将v插入到Lout (u)中，如果Lout (u)∩Lin (v) =∅。在迭代结束时，我们从Gk中删除v，并将结果图表示为Gk+1。在那之后，我们继续进行（k+1）次迭代。一旦所有的迭代都完成了，算法5返回所构建的标签集，它在G上形成一个TOL索引L。
正确性和复杂性。我们通过以下引理证明了算法5的正确性。

引理5。给定一个DAG G =（V，E）和一个顶点水平，算法5输出一个TOL索引为G。
证明。请注意，对于任意两个顶点u和v，算法5将u插入到标签内(中。只有当l (u) < l (v)和u可以达到v（v可以到达u）时。因此，算法5构建的索引从未违反定义1中的可归性或水平约束。
通过矛盾，假设算法5的输出不是一个TOL索引。然后，存在两个顶点u和v，这样(i) u在v的标签内或标签外标签中，并且（ii）u违反了路径约束。我们首先讨论u在v的标签内的情况，即u→v，同样的讨论也可以扩展到另一种情况。
由于u不满足路径约束，所以在从u到v的路径中存在一个顶点w，使得w的水平高于u和v的水平。如果存在好几条这样的路径，我们让w是在所有这些路径中级别最高的顶点。由于w的水平高于u和v的水平，所以w在去除u和v之前被删除。然后，当算法5删除w时，它必须将w添加到u的外标签集和v的标签内集中。现在注意到，当算法5删除u时，它将u添加到v的标签内集中，只有当Lout (u)∩Lin (v) =∅。然而，由于w已经被插入到Lout (u)和Lin (v)中，Lout (u)∩Lin (v) =∅。这说明你不应该在Lin (v)中，这导致了矛盾。
现在我们将讨论算法5的复杂性。设Gk =（Vk，Ek）为第k次迭代的输入图，用v表示Gk中顶点水平最高的顶点。正向和后向BFS的复杂度以|Ek|为界，B−(v)和B+(v)的总大小以|Vk|为界。此外，在第k次迭代中，任何顶点的标签内或标签外标签的大小最多为k，因为只有级别高于v的顶点被添加到当前标签中。因此，每个操作的复杂性，交集或加法，可以以O (k)为限制。总之，我们将k次迭代时的复杂度约束为O（|Ek| + k|Vk|）。注意，当我们在第k次迭代结束时从Gk中移除一个顶点时，用于计算的图就会变得越来越小，也就是说，当第k次迭代增加时，第k次迭代的复杂度显著降低。

8. EXPERIMENTS

本节通过实验来评估我们的解决方案。我们在C++中实现了我们的算法，并且我们采用了由其作者提供的所有竞争对手的C++实现。我们所有的实验都是在一台配备了IntelXeon2.4 GHz CPU和48GB内存的机器上进行的，运行着Ubuntu 12.4。在每个实验中，我们测量每种方法的性能5次，并报告平均测量值。如果一个方法需要超过24小时或超过48GB的RAM来预处理一个数据集D，我们将在D上的实验中省略该方法。
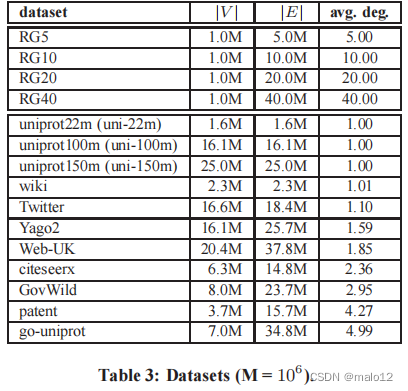
数据集和查询。表3显示了我们在实验中使用的数据集。其中，RG5、RG10、RG20和RG40是在[8]实验中使用该方法生成的合成的DAGs，将顶点的平均程度从5改变到40，将拓扑级别设置为8（详见[8]）。其他11个数据集是文献中采用的最大的dag。特别是22米，100米，150米，维，城市，和专利来自[8,17]，而GovWild、Yago2、推特和Web-英国则用于[25]。

在每个数据集G上，我们生成一组106个可达性查询。特别地，我们首先推导出G中顶点上的拓扑顺序。然后，对于每个查询q，我们从G中随机选择两个顶点，并选择具有较低的顶点。以拓扑秩作为源。顶点。t).这种查询生成方法确保了不可以通过简单地检查终端顶点是否具有低于源顶点1的拓扑秩来回答任何查询。
对于G上更新的每个实验，我们从G中随机删除104个顶点，并测量每种方法的平均删除时间。之后，我们将被删除的顶点插入回G中，其顺序与删除它们的顺序相反。在此过程中，我们计算了每个算法的平均插入时间。
动态图的实验。我们的第一组实验根据现有的动态图技术来评估我们的解决方案。如第3节中所述，有一些方法[4,12,13,16,22,24,32]用于处理可达性索引的更新。其中，[12,13,22]被限制为最多有几千个顶点[20]的小图，而[24]只处理XML图。我们测试了其余的方法，并发现在我们的实验中，只有Dagger [32]能够在多个数据集中运行。因此，我们选择匕首作为我们的竞争对手。此外，我们评估了我们的解决方案的两个版本，即蝴蝶U（BU）和蝴蝶L（BL），这样BU采用Sin和Sout作为其评分函数，BL采用S⊥in和S⊥out（见第7节）。
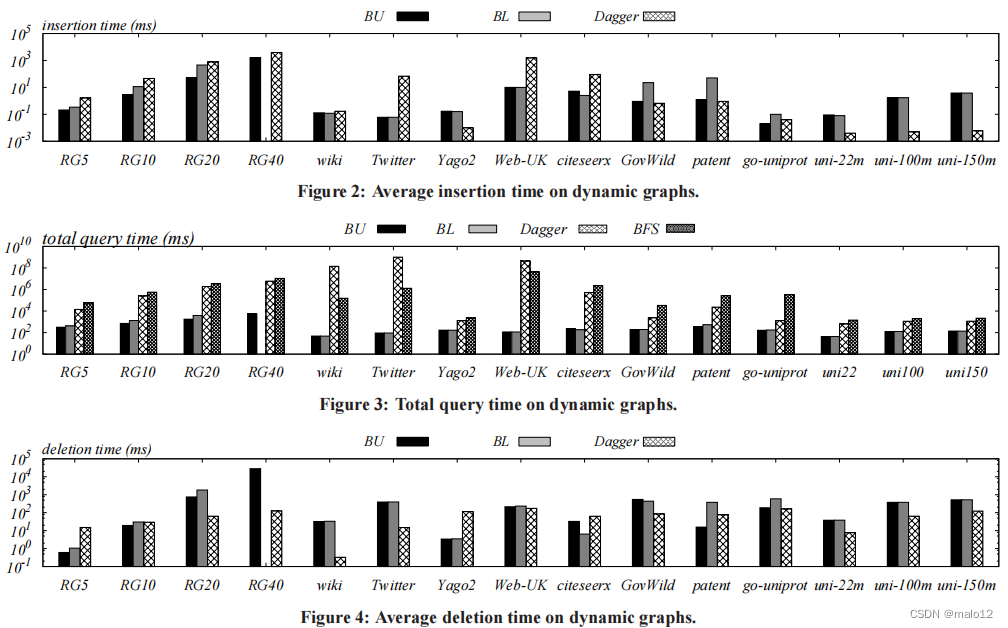
图2为BU、BL和Dagger的平均插入时间。请注意，在大多数情况下，BU比匕首更有效。特别是在推特上，Twitter的插入时间比Dagger低四个数量级。同时，BL的效率明显低于BU，尽管它在一半的数据集上仍然优于Dagger。（请注意，我们省略了RG40上的BL，因为它在图上导致了过多的内存消耗。）BU与BL之间的性能差距表明，BU采用的顶点排序优于BL。与此同时，Dagger在22米、100米和150米的水平上都显著优于BU和BL(i)这三个图中的每一个都是一个树，并且（ii）Dagger对树[32]特别有效。
图3说明了BU、BL、Dagger的总查询时间（对于处理106个查询），以及一个简单的基线方法。特别地，给定图G上的可达性查询q，基线方法从q的源顶点（跟随每个顶点的出边）执行BFS，以及从q的终端顶点执行BFS（跟随每个顶点的入边）执行BFS。两个BFSs轮流遍历G中的顶点，直到两个BFSs都访问了一个共同的顶点（即，当找到从源顶点到终端顶点的路径时）。如图3所示，BU的性能始终优于Dagger和BFS方法，并且BL的查询时间一般比BU的略差。另一方面，Dagger在大多数数据集上只比BFS方法稍微好一些，并且超过了900个方法。比Wiki上的速度慢700倍。在推特上的)。这表明Dagger不是处理动态图更新的有利方法，因为它比BFS方法产生了高得多的更新开销，但没有提供更好的查询性能。（请注意，BFS方法需要零更新成本，因为它不维护任何索引。）
最后，图4显示了每种方法的平均删除时间。除了RG40和wiki外，BU和BL的性能一般与Dagger相当。BU在删除方面的性能略差，这是因为它在插入和查询方面的效率更优越。

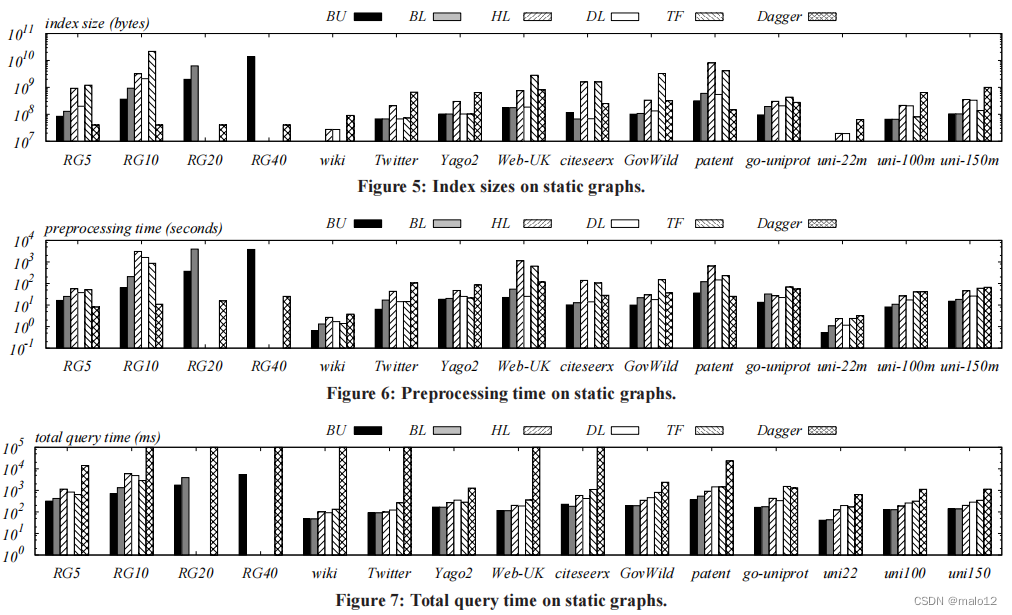
静态图的实验。我们的第二组实验比较了BU和BL与三种最先进的静态图方法，即TF-label（TF）[8]、层次标记（HL）[17]、分布标记（DL）[17]。为了完整起见，我们在实验中还加入了匕首。图5说明了每种方法的空间消耗情况。观察到BU和BL一般都优于TF和DL。为了解释，请记住BU、BL、TF和DL都是TOL框架的实例化。因此，它们的性能完全由它们所采用的顶点顺序决定。DL中的顶点排序。然而，它只是简单地根据顶点的程度（拓扑等级）来对顶点进行排序。相比之下，BU和BL都基于考虑到输入图特征的高级评分函数对顶点进行排序。因此，BU和BL所采用的顶点排序优于TF和DL，从而导致索引尺寸更小。特别是在RG10上，BU的空间开销比DL小5倍。同时，HL的空间代价总是高于DL，这与[17]的实验结果一致。
图6说明了每种方法的预处理时间。BU、BL、TF、HL、DL的相对性能与图5的情况相似，因为索引尺寸越小，说明标签集中的标签越少，因此标签集的建设成本一般较小。我们省略了RG20和RG40上的HL和DL，因为它们在这些图上的内存消耗超过了48GB。在RG10上，HL、DL和TF的预处理成本至少比BU高一个数量级，说明前者对输入图的平均度更为敏感。图7绘制了每个算法对106个随机查询的总查询时间。同样，由于BU和BL的顶点顺序有所改进，它们始终优于TF和DL。特别是在RG10上，BU的查询时间为4。是TF的7倍。分升同时，HL的查询成本与DL相当。

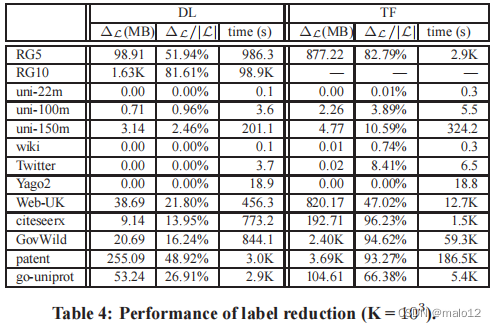
标签减少实验。我们的最后一组实验评估了在第6节中提出的标签缩减方法。具体来说，我们首先使用DL和TF来构建可达性索引然后在L上应用我们的标签缩减算法，得到一个改进的指标L∗。然后，我们测量L的∗和L的大小之间的差值ΔL，然后我们将ΔL除以L的大小来得到空间缩减的比率。观察到DL和TF的空间减少率分别为81.61%和96.23%。这证明了我们的标签减少方法的有效性。然而，标签减少过程在一些图形（例如，专利）上产生了显著的计算开销。这表明，人们不应该过度依赖标签缩减方法来提高TOL指数的性能，而是应该采用一个良好的初始顶点顺序（例如，BU和BL所采用的顺序）。注意，RG10上的TF没有结果，因为标签减少过程在图上花费了过多的时间。此外，我们在实验中省略了RG20和RG40，因为DL和TF在这两个数据集上都产生了禁止的内存消耗。

9. CONCLUSIONS

本文对大型动态图上的可达性查询进行了一种新的研究。我们提出了处理可达性指数上的顶点插入和删除的一般和有效的算法，并证明了我们的算法也可以用于提高现有的静态图技术的性能。此外，我们还设计了一种新的算法，从头开始在输入图上构造一个有效的可达性索引。我们在一大批的真实图和合成图上评估了我们的解决方案，并证明了我们的解决方案不仅支持对大型动态图的有效更新，而且还提供了比最先进的静态图技术更好的查询性能。据我们所知，我们是文献中第一个提出可达性索引，可以有效地处理更新，同时提供优越的查询性能。在未来的工作中，我们计划研究如何将我们的解决方案扩展到不适合主存的大量图。

这篇关于【论文阅读】Reachability Queries on Large Dynamic Graphs: A Total Order Approach的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---