本文主要是介绍【数据结构第 6 章 ③】- 用 C 语言实现邻接表并简单介绍十字链表和邻接多重表,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、邻接表
1.1 - ALGraph.h
1.2 - ALGraph.c
1.3 - Test.c
二、十字链表
三、邻接多重表
一、邻接表
邻接表(Adjacency List)是图的一种链式存储结构。在邻接表中,对图中每个顶点建立一个单链表,第 i 个单链表中的结点表示依附于顶点 vi 的边(对有向图是以顶点 vi 为尾的弧)。每个结点由 3 个域组成,其中邻接顶点域(adjVexPos)指示与顶点 vi 邻接的顶点在图中的位置,链域(nextEdge)指示下一条边(或弧)的结点;数据域(info)存储和边(或弧)相关的信息,如权值等。
在表头结点中,除了设有链域(firstEdge)指向链表中的第一个结点之外,还设有存储顶点 vi 的名称或其他有关信息的数据域(vertex)。这些表头结点通常以顺序结构的形式存储,以便随机访问任一顶点的边链表。
下图 (a) 和 (b) 所示为图一中 G1 和 G2 的邻接表。

在无向图的邻接表中,顶点 vi 的度恰为第 i 个链表中的结点数;而在有向图中,第 i 个链表中的结点个数只是顶点 vi 的出度,为求入度,必须遍历整个邻接表。在所有链表中,其邻接顶点域的值为 i 的结点个数是顶点 vi 的入度。有时,为了便于确定顶点的入度,可以建立一个有向图的逆邻接表,即对每个顶点 vi 建立一个链接所有进入 vi 的边的表。
下图 (c) 所示为图一中有向图 G1 的逆邻接表。

1.1 - ALGraph.h
注意:下面是以无向图为例的。
#pragma once#define DEFAULT_CAPACITY 10typedef char VertexType;typedef struct EdgeNode
{int adjVexPos;struct EdgeNode* nextEdge;
}EdgeNode;typedef struct VertexNode
{VertexType vertex;EdgeNode* firstEdge;
}VertexNode;typedef struct ALGraph
{VertexNode* vertices;int vSize;int eSize;int capacity;
}ALGraph;// 基本操作
void ALGraphInit(ALGraph* pg); // 初始化void ShowAdjList(ALGraph* pg); // 显示邻接表int GetVertexPos(ALGraph* pg, VertexType v); // 获取顶点的位置void InsertVertex(ALGraph* pg, VertexType v); // 插入顶点
void InsertEdge(ALGraph* pg, VertexType v1, VertexType v2); // 插入边void EraseVertex(ALGraph* pg, VertexType v); // 删除顶点
void EraseEdge(ALGraph* pg, VertexType v1, VertexType v2); // 删除边int GetFirstAdjVexPos(ALGraph* pg, VertexType v); // 获取 v 的第一个邻接顶点的位置
int GetNextAdjVexPos(ALGraph* pg, VertexType v, VertexType w);
// 获取 v 的(相对于 w)的下一个邻接顶点的位置void ALGraphDestroy(ALGraph* pg); // 销毁1.2 - ALGraph.c
-
初始化:
void ALGraphInit(ALGraph* pg) {assert(pg);pg->vSize = pg->eSize = 0;pg->capacity = DEFAULT_CAPACITY;pg->vertices = (VertexNode*)malloc(sizeof(VertexNode) * pg->capacity);assert(pg->vertices);for (int i = 0; i < pg->capacity; ++i){pg->vertices[i].firstEdge = NULL;} } -
显示邻接表:
void ShowAdjList(ALGraph* pg) {assert(pg);for (int i = 0; i < pg->vSize; ++i){printf("%d %c:>", i, pg->vertices[i].vertex);EdgeNode* cur = pg->vertices[i].firstEdge;while (cur){printf("%d-->", cur->adjVexPos);cur = cur->nextEdge;}printf("NULL\n");} } -
获取顶点的位置:
int GetVertexPos(ALGraph* pg, VertexType v) {assert(pg);for (int i = 0; i < pg->vSize; ++i){if (pg->vertices[i].vertex == v)return i;}return -1; } -
插入顶点:
void InsertVertex(ALGraph* pg, VertexType v) {assert(pg);// 考虑是否需要扩容if (pg->vSize == pg->capacity){VertexNode* tmp = (VertexNode*)realloc(pg->vertices, sizeof(VertexNode) * 2 * pg->capacity);assert(tmp);pg->vertices = tmp;for (int i = pg->capacity; i < 2 * pg->capacity; ++i){pg->vertices[i].firstEdge = NULL;}pg->capacity *= 2;}// 插入顶点pg->vertices[pg->vSize++].vertex = v; } -
插入边:
void InsertEdge(ALGraph* pg, VertexType v1, VertexType v2) {assert(pg);int pos1 = GetVertexPos(pg, v1);int pos2 = GetVertexPos(pg, v2);if (pos1 == -1 || pos2 == -1)return;// 插入 (v1, v2)EdgeNode* p = (EdgeNode*)malloc(sizeof(EdgeNode));assert(p);p->adjVexPos = pos2;// 头插p->nextEdge = pg->vertices[pos1].firstEdge;pg->vertices[pos1].firstEdge = p;// 插入 (v2, v1)p = (EdgeNode*)malloc(sizeof(EdgeNode));assert(p);p->adjVexPos = pos1;// 头插p->nextEdge = pg->vertices[pos2].firstEdge;pg->vertices[pos2].firstEdge = p;++pg->eSize; // 注意:边数只需要加 1 } -
删除顶点:
// 删除顶点 void EraseVertex(ALGraph* pg, VertexType v) {assert(pg);int pos = GetVertexPos(pg, v);if (pos == -1)return;// 第一步:删除和顶点 v 相关联的边EdgeNode* cur = pg->vertices[pos].firstEdge;while (cur){// 找到邻接顶点 v2, 先删除 (v2, v)int pos2 = cur->adjVexPos;EdgeNode* prev2 = NULL;EdgeNode* cur2 = pg->vertices[pos2].firstEdge;while (cur2 && cur2->adjVexPos != pos){prev2 = cur2;cur2 = cur2->nextEdge;}if (cur2){if (prev2 == NULL)pg->vertices[pos2].firstEdge = cur2->nextEdge;elseprev2->nextEdge = cur2->nextEdge;free(cur2);}// 再删除 (v, v2)pg->vertices[pos].firstEdge = cur->nextEdge;free(cur);cur = pg->vertices[pos].firstEdge;--pg->eSize; // 注意不要遗漏}// 第二步:删除顶点 vpg->vertices[pos].vertex = pg->vertices[pg->vSize - 1].vertex;pg->vertices[pos].firstEdge = pg->vertices[pg->vSize - 1].firstEdge;cur = pg->vertices[pos].firstEdge;while (cur){int pos2 = cur->adjVexPos;EdgeNode* cur2 = pg->vertices[pos2].firstEdge;while (cur2){if (cur2->adjVexPos == pg->vSize - 1){cur2->adjVexPos = pos;break;}cur2 = cur2->nextEdge;}cur = cur->nextEdge;}--pg->vSize; // 注意不要遗漏 } -
删除边:
void EraseEdge(ALGraph* pg, VertexType v1, VertexType v2) {assert(pg);int pos1 = GetVertexPos(pg, v1);int pos2 = GetVertexPos(pg, v2);if (pos1 == -1 || pos2 == -1)return;// 删除 (v1, v2)EdgeNode* prev = NULL;EdgeNode* cur = pg->vertices[pos1].firstEdge;while (cur && cur->adjVexPos != pos2){prev = cur;cur = cur->nextEdge;}if (cur == NULL) // 说明 (v1, v2) 不存在 return;if (prev == NULL)pg->vertices[pos1].firstEdge = cur->nextEdge;elseprev->nextEdge = cur->nextEdge;free(cur);// 删除 (v2, v1)// 注意:此时 (v2, v1) 一定存在prev = NULL;cur = pg->vertices[pos2].firstEdge;while (cur->adjVexPos != pos1){prev = cur;cur = cur->nextEdge;}if (prev == NULL)pg->vertices[pos2].firstEdge = cur->nextEdge;elseprev->nextEdge = cur->nextEdge;free(cur);--pg->eSize; // 注意不要遗漏 } -
获取 v 的第一个邻接顶点的位置:
int GetFirstAdjVexPos(ALGraph* pg, VertexType v) {assert(pg);int pos = GetVertexPos(pg, v);if (pos == -1)return -1;EdgeNode* cur = pg->vertices[pos].firstEdge;if (cur)return cur->adjVexPos;elsereturn -1; } -
获取 v 的(相对于 w)的下一个邻接顶点的位置:
int GetNextAdjVexPos(ALGraph* pg, VertexType v, VertexType w) {assert(pg);int pos1 = GetVertexPos(pg, v);int pos2 = GetVertexPos(pg, w);if (pos1 == -1 || pos2 == -1)return -1;EdgeNode* cur = pg->vertices[pos1].firstEdge;while (cur && cur->adjVexPos != pos2){cur = cur->nextEdge;}if (cur && cur->nextEdge)return cur->nextEdge->adjVexPos;elsereturn -1; } -
销毁:
void ALGraphDestroy(ALGraph* pg) {assert(pg);for (int i = 0; i < pg->vSize; ++i){EdgeNode* cur = pg->vertices[i].firstEdge;while (cur){// 头删pg->vertices[i].firstEdge = cur->nextEdge;free(cur);cur = pg->vertices[i].firstEdge;}}free(pg->vertices);pg->vertices = NULL;pg->vSize = pg->eSize = pg->capacity = 0; }
1.3 - Test.c
#include "ALGraph.h"
#include <stdio.h>int main()
{ALGraph g;ALGraphInit(&g);InsertVertex(&g, 'A');InsertVertex(&g, 'B');InsertVertex(&g, 'C');InsertVertex(&g, 'D');InsertVertex(&g, 'E');InsertEdge(&g, 'A', 'B');InsertEdge(&g, 'A', 'D');InsertEdge(&g, 'B', 'C');InsertEdge(&g, 'B', 'E');InsertEdge(&g, 'C', 'D');InsertEdge(&g, 'C', 'E');ShowAdjList(&g);printf("\n");EraseVertex(&g, 'C');ShowAdjList(&g);printf("\n");EraseEdge(&g, 'A', 'B');ShowAdjList(&g);printf("\n");printf("%d\n", GetFirstAdjVexPos(&g, 'A')); // 3printf("%d\n", GetNextAdjVexPos(&g, 'A', 'D')); // -1ALGraphDestroy(&g);return 0;
}
二、十字链表
十字链表(Orthogonal List)是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中,对应于有向图中的每一条弧有一个结点,对应于每个顶点也有一个结点。这些结点的结构如下图所示。

在弧结点中有 5 个域:其中尾域(tailvex)和头域(headvex)分别指示弧尾和弧头这两个顶点在图中的位置,链域 hlink 指向弧头相同的下一条弧,而链域 tlink 指向弧尾相同的下一条弧,info 域指向该弧的相关信息。弧头相同的弧在同一链表上,弧尾相同的弧也在同一链表上。
它们的头结点即为顶点结点,它由 3 个域组成:其中 data 域存储和顶点相关的信息,如顶点的名称等;firstin 和 firstout 为两个链域,分别指向以该顶点为弧头或弧尾的第一个弧结点。
例如下图 (a) 中所示的图的十字链表如下图 (b) 所示。

三、邻接多重表
邻接多重表(Adjacency Multilist)是无向图的另一种链式存储结构。虽然邻接表是无向图的一种有效的存储结构,在邻接表中容易求得顶点和边的各种信息,但是在邻接表中每一条边 有两个结点,分别在第 i 个和第 j 个链表中,这给某些图的操作带来不便,例如在某些图的应用问题中需要对边进行某种操作,如对已被搜索过的边做记号或删除一条边等,此时需要找到表示同一条边的两个结点。因此,在进行这一类操作的无向图的问题中采用邻接多重表更为适宜。
邻接多重表的结构和十字链表类似,在邻接多重表中,每一条边用一个结点表示,它由下图 (a) 所示的 6 个域组成。其中 mark 为标志域,可用以标记该条边是否被搜索过;ivex 和 jvex 为该边依附的两个顶点在图中的位置;ilink 指向下一条依附于顶点 ivex 的边;jlink 指向下一条依附于顶点 jvex 的边,info 为指向和边相关的各种信息的指针域。
每个顶点也用一个结点表示,它由下图 (b) 所示的 2 个域组成。其中,data 域存储和该顶点相关的信息;firstedge 域指示第一条依附于该顶点的边。

例如下图所示为图一中无向图 G2 的邻接多重表。
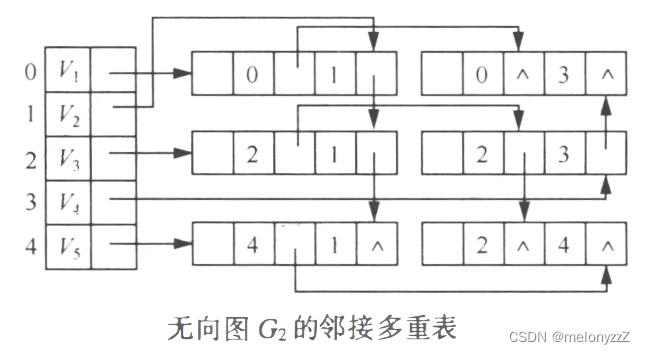
在邻接多重表中,所有依附于同一顶点的边串联在同一链表中,由于每条边依附于两个顶点,则每个边结点同时链接在两个链表中。可见,对于无向图而言,其邻接多重表和邻接表的差别,仅仅在于同一条边在邻接表中用两个结点表示,而在邻接多重表中只有一个结点。因此,除了在边结点中增加一个标志域外,邻接多重表所需的存储量和邻接表相同。
这篇关于【数据结构第 6 章 ③】- 用 C 语言实现邻接表并简单介绍十字链表和邻接多重表的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






