本文主要是介绍【进程代数学习笔记】4:[CSP]进程间的通道通信,管道与活锁避免,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 记号
1.1 通道和数据
同系统分析与验证课上学的Channel system记号类似,CSP中用序偶 c . v c.v c.v(参见笔记一的2.14)表示在通道 c c c上传送数据 v v v。则进程 P P P能够在通道 c c c上通信的数据记为:
α c ( P ) = { v ∣ c . v ∈ α P } \alpha c(P) = \{v \ | \ c.v \in \alpha P \} αc(P)={v ∣ c.v∈αP}
用 c h a n n e l ( ) channel() channel()和 m e s s a g e ( ) message() message()分别表示取通道名和取数据:
c h a n n e l ( c . v ) = c m e s s a g e ( c . v ) = v channel(c.v) = c \\ message(c.v) = v channel(c.v)=cmessage(c.v)=v
1.2 数据上通道
一进程将数据 v ∈ α c ( P ) v \in \alpha c(P) v∈αc(P)发送到通道 c c c上,接下来执行 P P P,记为:
( c ! v → P ) = ( c . v → P ) (c!v \to P) = (c.v \to P) (c!v→P)=(c.v→P)
1.3 从通道取数据
一进程从通道 c c c取下一个数据 x x x,并根据收到的 x x x的不同决定接下来的执行 P ( x ) P(x) P(x),记为:
( c ? x → P ( x ) ) = ( y : { y ∣ c h a n n e l ( y ) = c } → P ( m e s s a g e ( y ) ) ) (c?x \to P(x)) = (y: \{y \ | \ channel(y) = c \} \to P(message(y)) \ ) (c?x→P(x))=(y:{y ∣ channel(y)=c}→P(message(y)) )
式中 y y y表示通道 c c c上传递 m e s s a g e ( y ) message(y) message(y)的序偶,如 c . 7 c.7 c.7。
例如,拷贝一比特数据的进程 C O P Y B I T COPYBIT COPYBIT,可理解成从 i n in in通道取 v ∈ { 0 , 1 } v \in \{0,1\} v∈{0,1},再发送到 o u t out out通道上:
C O P Y B I T = μ X ⋅ ( i n ? x → ( o u t ! x → X ) ) COPYBIT = \mu X \cdot (in?x \to (out!x \to X)) COPYBIT=μX⋅(in?x→(out!x→X))
其中 α i n ( C O P Y B I T ) = α o u t ( C O P Y B I T ) = { 0 , 1 } \alpha in(COPYBIT) = \alpha out (COPYBIT) = \{0,1\} αin(COPYBIT)=αout(COPYBIT)={0,1}。
1.4 进程间使用通道通信
这里要注意和系统分析课使用的记号不同,这里就是用普通的并发" ∣ ∣ || ∣∣"记号, P ∣ ∣ Q P||Q P∣∣Q当 P P P发送数据到通道 c c c(即 c ! v c!v c!v),而 Q Q Q从通道 c c c上取数据(即 c ? x c?x c?x)时,两进程就会发送通信。例如发送的数据是7,即是说 P P P执行的动作是 c ! 7 c!7 c!7, Q Q Q推进的动作是 c ? 7 → Q ( 7 ) c?7 \to Q(7) c?7→Q(7)。
总是要求通道两侧的进程在通道上传值的字母表一致,即 α c ( P ) = α c ( Q ) \alpha c(P) = \alpha c(Q) αc(P)=αc(Q),不妨记为 α c \alpha c αc。
通道通信中的字母表是关于通道名称的字母表!
2 几个例子
在CSP里的通信模型中,进程的下标表达了进程状态的互递归关系,其指示的是进程收到的通道中的值(还未传出去的那些)。
2.1 数据处理单元
这个例子用于理解在引入通道通信后,进程如何表达数据处理单元。这里是直接将数据乘以2:
D O U B L E = μ X ⋅ ( l e f t ? x → r i g h t ! ( x + x ) → X ) DOUBLE = \mu X \cdot (left?x \to right!(x+x) \to X) DOUBLE=μX⋅(left?x→right!(x+x)→X)
2.2 序列拆分
从 l e f t left left通道一次性读入长度为80的数据,从 r i g h t right right通道一次输出一个(队头):
α l e f t = { s ∣ s ∈ α r i g h t ∗ ∧ # x = 80 } U N P A C K = P ⟨ ⟩ P ⟨ ⟩ = l e f t ? s → P s P ⟨ x ⟩ = r i g h t ! x → P ⟨ ⟩ P ⟨ x ⟩ ⌢ s = r i g h t ! x → P s \begin{aligned} \alpha left &= \{s \ | \ s\in \alpha right^* \wedge \#x = 80 \} \\ UNPACK &= P_{\langle \rangle} \\ \\ P_{\langle \rangle} & = left?s \to P_s \\ P_{\langle x \rangle} & = right!x \to P_{\langle \rangle} \\ P_{\langle x \rangle^\smallfrown s} & = right!x \to P_s \end{aligned} αleftUNPACKP⟨⟩P⟨x⟩P⟨x⟩⌢s={s ∣ s∈αright∗∧#x=80}=P⟨⟩=left?s→Ps=right!x→P⟨⟩=right!x→Ps
2.3 序列合并
从 l e f t left left通道每次读入一个数据,到125个时从 r i g h t right right通道一次性输出:
α r i g h t = { s ∣ s ∈ α l e f t ∗ ∧ # s = 125 } P A C K = P ⟨ ⟩ P s = r i g h t ! s → P ⟨ ⟩ i f # s = 125 P s = l e f t ? x → P s ⌢ ⟨ x ⟩ i f # s < 125 \begin{aligned} \alpha right & = \{s \ | \ s \in \alpha left^* \wedge \#s = 125 \} \\ PACK & = P_{\langle \rangle} \\ \\ P_s & = right!s \to P_{\langle \rangle} & if \ \#s=125 \\ P_s & = left?x \to P_{s^\smallfrown \langle x \rangle} & if \ \#s<125 \end{aligned} αrightPACKPsPs={s ∣ s∈αleft∗∧#s=125}=P⟨⟩=right!s→P⟨⟩=left?x→Ps⌢⟨x⟩if #s=125if #s<125
2.4 子串替换
这个例子有点编译器的味道,就是把" ∗ ∗ ** ∗∗“输出成” ↑ \uparrow ↑",其它都不变,显然要在输入了一个" ∗ * ∗"时检查下一个输入:
α l e f t = α r i g h t − { " ↑ " } S Q U A S H = μ X ⋅ l e f t ? x → i f x ≠ " ∗ " t h e n ( r i g h t ! x → X ) e l s e l e f t ? y → i f y = " ∗ " t h e n ( r i g h t ! " ↑ " → X ) e l s e ( r i g h t ! " ∗ " → r i g h t ! y → X ) ) \begin{aligned} \alpha left & = \alpha right - \{"\uparrow"\} \\ SQUASH & = \mu X \cdot left?x \to \\ if \ x & \neq "*" \ then \ (right!x \to X) \\ else \ &left?y \to \\ & if \ y="*" \ then \ (right!"\uparrow" \to X) \\ & else \ (right!"*" \to right!y \to X)) \end{aligned} αleftSQUASHif xelse =αright−{"↑"}=μX⋅left?x→="∗" then (right!x→X)left?y→if y="∗" then (right!"↑"→X)else (right!"∗"→right!y→X))
2.4 可选输入
一个双输入管道,但每次只选其一,然后就原样输出的进程:
α l e f t 1 = α l e f t 2 = α r i g h t M E R G E = ( l e f t 1 ? x → r i g h t ! x → M E R G E ∣ l e f t 2 ? x → r i g h t ! x → M E R G E ) \begin{aligned} \alpha left1 = & \alpha left2 = \alpha right \\ MERGE =& (left1?x \to right!x \to MERGE \\ & | \ left2?x \to right!x \to MERGE) \end{aligned} αleft1=MERGE=αleft2=αright(left1?x→right!x→MERGE∣ left2?x→right!x→MERGE)
显然,输出可以是两个输入序列的任一Interleaving。
2.5 一位寄存器
总是可以读入一个数据将当前数据覆盖掉,或者输出寄存的数据而不会因输出导致丢失数据:
α l e f t = α r i g h t V A R = l e f t ? x → V A R x V A R x = ( l e f t ? y → V A R y ∣ r i g h t ! x → V A R x ) \begin{aligned} \alpha left & = \alpha right \\ VAR & = left?x \to VAR_x \\ VAR_x & = (left?y \to VAR_y \ | \ right!x \to VAR_x) \end{aligned} αleftVARVARx=αright=left?x→VARx=(left?y→VARy ∣ right!x→VARx)
2.6 多参数计算单元
从 u p up up通道读入prod,从 l e f t left left通道读入sum,计算 s u m + v × p r o d sum+v \times prod sum+v×prod的进程:
N O D E ( v ) = μ X ⋅ ( u p ? s u m → l e f t ? p r o d → d o w n ! ( s u m + v × p r o d ) → X ) NODE(v) = \mu X \cdot (up?sum \to left?prod \to down!(sum+v \times prod) \to X) NODE(v)=μX⋅(up?sum→left?prod→down!(sum+v×prod)→X)
2.7 无限容量的队列
注意2.7和2.8模拟栈和队列都是在用进程模拟,而不是在用通道模拟。通道本身就是一个队列,在CSP里忽视通道的容量。
读入元素放到队尾,出队时去除队头元素:
B U F F E R = P ⟨ ⟩ P ⟨ ⟩ = l e f t ? x → P ⟨ x ⟩ P ⟨ x ⟩ ⌢ s = ( l e f t ? y → P ⟨ x ⟩ ⌢ s ⌢ ⟨ y ⟩ ∣ r i g h t ! x → P x ) \begin{aligned} BUFFER & = P_{\langle \rangle} \\ \\ P_{\langle \rangle} & = left?x \to P_{\langle x \rangle} \\ P_{\langle x \rangle^\smallfrown s} & = (left?y \to P_{\langle x \rangle^\smallfrown s^\smallfrown \langle y \rangle} \ | \ right!x \to P_x) \end{aligned} BUFFERP⟨⟩P⟨x⟩⌢s=P⟨⟩=left?x→P⟨x⟩=(left?y→P⟨x⟩⌢s⌢⟨y⟩ ∣ right!x→Px)
2.8 无限容量的栈
读入元素放到栈顶,出栈时去除栈顶元素:
S T A C K = P ⟨ ⟩ P ⟨ ⟩ = l e f t ? x → P ⟨ x ⟩ P ⟨ x ⟩ ⌢ s = ( l e f t ? y → P ⟨ y ⟩ ⌢ ⟨ x ⟩ ⌢ s ∣ r i g h t ! x → P x ) \begin{aligned} STACK & = P_{\langle \rangle} \\ \\ P_{\langle \rangle} & = left?x \to P_{\langle x \rangle} \\ P_{\langle x \rangle^\smallfrown s} & = (left?y \to P_{\langle y \rangle^\smallfrown \langle x \rangle^\smallfrown s} \ | \ right!x \to P_x) \end{aligned} STACKP⟨⟩P⟨x⟩⌢s=P⟨⟩=left?x→P⟨x⟩=(left?y→P⟨y⟩⌢⟨x⟩⌢s ∣ right!x→Px)
3 通道满足规范(specification)
3.1 简述
定义迹 t r tr tr中在有关通道 c c c的所有动作的值 v v v组成的迹:
t r ↓ c = m e s s a g e ∗ ( t r ↾ α c ) tr \downarrow c = message^*(tr \upharpoonright \alpha c) tr↓c=message∗(tr↾αc)
输入通道和输出通道的迹之间往往可以存在序关系(一方是另一方的前缀):
t r ↓ r i g h t ≤ t r ↓ l e f t tr \downarrow right \leq tr \downarrow left tr↓right≤tr↓left
简写成 r i g h t ≤ l e f t right \leq left right≤left。所以:
s ≤ n t = ( s ≤ t ∧ # t ≤ # s + n ) s \leq^n t = (s \leq t \wedge \# t \leq \# s+n) s≤nt=(s≤t∧#t≤#s+n)
这表示,通道 s s s(的trace)是通道 t t t(的trace)的前缀,并且 t t t(的trace)最多比 s s s(的trace)长n。这可导出如下性质:
- s ≤ 0 t ≡ ( s = t ) s \leq^0 t \equiv (s = t) s≤0t≡(s=t)
最多长0说明一样长,又是前缀说明它们的trace就是一样的。 - s ≤ n t ∧ t ≤ m u ⇒ s ≤ n + m u s \leq^n t \wedge t \leq^m u \Rightarrow s \leq^{n+m} u s≤nt∧t≤mu⇒s≤n+mu
这是由前缀的传递性和不等式的合并。 - s ≤ t ≡ ∃ n ⋅ s ≤ n t s \leq t \equiv \exists n \cdot s \leq^n t s≤t≡∃n⋅s≤nt
前缀关系总是会有长度关系的界。
3.2 例子
在1.3中的 C O P Y B I T COPYBIT COPYBIT满足:
C O P Y B I T s a t r i g h t ≤ 1 l e f t COPYBIT \ sat \ right \leq^1 left COPYBIT sat right≤1left
右边总是左边的前缀,且左边比右边最多长1,仅当刚输入还没开始输出时取等号。
在2.1中的 D O U B L E DOUBLE DOUBLE满足:
D O U B L E s a t r i g h t ≤ 1 d o u b l e ∗ ( l e f t ) DOUBLE \ sat \ right \leq^1 double^*(left) DOUBLE sat right≤1double∗(left)
这在本质上和上一个是一样的,式中" d o u b l e ∗ ( ) double^*() double∗()"仅仅是一个将传入的trace中每个数字乘2的符号变换而已。
在2.2中的 U N P A C K UNPACK UNPACK满足:
U N P A C K s a t r i g h t ≤ 80 ⌢ / l e f t UNPACK \ sat \ right \leq^{80} \smallfrown / left UNPACK sat right≤80⌢/left
其中 ⌢ / \smallfrown / ⌢/后接一个序列,作用是将其中的所有元素连接成一个合乎规格的普通trace:
⌢ / ⟨ s 0 , s 1 , . . . , s n − 1 ⟩ = s 0 ⌢ s 1 ⌢ . . . ⌢ s n − 1 \smallfrown / \langle s_0, s_1, ... , s_{n-1} \rangle = s_0^\smallfrown s_1^\smallfrown ... ^\smallfrown s_{n-1} ⌢/⟨s0,s1,...,sn−1⟩=s0⌢s1⌢...⌢sn−1
上面是课本中的写法,意思就是trace里包含trace,实际上在这个例子和下一个例子里都只包含一个 s 0 s_0 s0,这里 # s 0 = 80 \# s_0 = 80 #s0=80,下个例子里 # s 0 = 125 \# s_0 = 125 #s0=125。
在2.3中的 P A C K PACK PACK满足:
P A C K s a t ( ( ⌢ / r i g h t ≤ 125 l e f t ) ∧ ( # ∗ r i g h t ∈ { 125 } ∗ ) ) PACK \ sat \ (( \smallfrown / right \leq^{125} left) \wedge ( \#^* right \in \{125\}^*)) PACK sat ((⌢/right≤125left)∧(#∗right∈{125}∗))
4 通信(Communication)
4.1 简述
进程间可以依靠通道上发送和接受值来实现通信:
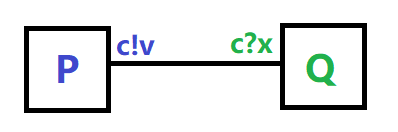
如上图中若 v = 7 v=7 v=7,则进程 Q Q Q也就收到 x = 7 x=7 x=7,然后执行 Q ( 7 ) Q(7) Q(7)。
-
L1: ( c ! v → P ) ∣ ∣ ( c ? x → Q ( x ) ) = c ! v → ( P ∣ ∣ Q ( v ) ) (c!v \to P) \ || \ (c?x \to Q(x)) = c!v \to (P \ || \ Q(v)) (c!v→P) ∣∣ (c?x→Q(x))=c!v→(P ∣∣ Q(v))
传递的信息 v v v决定后续动作。 -
L2: ( ( c ! v → P ) ∣ ∣ ( c ? x → Q ( x ) ) ) \ C = ( P ∣ ∣ Q ( v ) ) \ C ((c!v \to P) \ || \ (c?x \to Q(x))) \backslash C = (P \ || \ Q(v)) \backslash C ((c!v→P) ∣∣ (c?x→Q(x)))\C=(P ∣∣ Q(v))\C
这是将通道上的通讯动作屏蔽掉,其中通道动作集合 C = { c . v ∣ v ∈ α c } C = \{c.v \ | \ v\in \alpha c\} C={c.v ∣ v∈αc}。
4.2 例子

P = ( l e f t ? x → m i d ! ( x × x ) → P ) Q = ( m i d ? y → r i g h t ! ( 173 × y ) → Q ) \begin{aligned} P & = (left?x \to mid!(x \times x) \to P) \\ Q & = (mid?y \to right!(173 \times y) \to Q) \end{aligned} PQ=(left?x→mid!(x×x)→P)=(mid?y→right!(173×y)→Q)
其中, P P P和 Q Q Q各自满足的规格:
P s a t ( m i d ≤ 1 s q u a r e ∗ ( l e f t ) ) Q s a t ( r i g h t ≤ 1 173 × m i d ) \begin{aligned} P \ & sat \ (mid \leq^1 square^*(left)) \\ Q \ & sat \ (right \leq^1 173 \times mid) \end{aligned} P Q sat (mid≤1square∗(left))sat (right≤1173×mid)
两进程并发,所有满足的规格要取合取:
( P ∣ ∣ Q ) s a t ( r i g h t ≤ 1 173 × m i d ) ∧ ( m i d ≤ 1 s q u a r e ∗ ( l e f t ) ) (P \ || \ Q) \ sat \ (right \leq^1 173 \times mid) \wedge (mid \leq^1 square^*(left)) (P ∣∣ Q) sat (right≤1173×mid)∧(mid≤1square∗(left))
从而:
r i g h t ≤ 173 × s q u a r e ∗ ( l e f t ) right \leq 173 \times square^*(left) right≤173×square∗(left)
5 管道(Pipes)
5.1 简述
管道是一系列进程的顺序组合,这些进程之间通信的通道被屏蔽掉,即外部无法看到管道内部的具体通信过程,如将4.1中两进程间的通信过程隐藏:
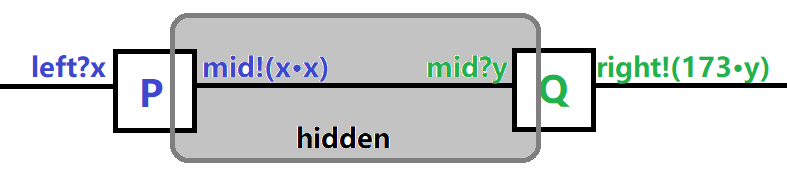
记为 P > > Q P>>Q P>>Q,管道的字母表:
α ( P > > Q ) = α l e f t ( P ) ∪ α r i g h t ( P ) \begin{aligned} \alpha(P>>Q) & = \alpha left(P) \cup \alpha right(P) \\ \end{aligned} α(P>>Q)=αleft(P)∪αright(P)
5.2 例子
通过组合不同的进程,可以构造出具有各式各样功能的管道。
-
X1: Q U A D R U P L E = D O U B L E > > D O U B L E QUADRUPLE = DOUBLE >> DOUBLE QUADRUPLE=DOUBLE>>DOUBLE
将输入数据放大四倍的管道。 -
X2: U N P A C K > > P A C K UNPACK >> PACK UNPACK>>PACK
80到125的序列长度转换器。 -
X3: U N P A C K > > S Q U A S H > > P A C K UNPACK >> SQUASH >> PACK UNPACK>>SQUASH>>PACK
类似于X2,只是还要在转换过程中将" ∗ ∗ ** ∗∗“过滤为” ↑ \uparrow ↑"。 -
X4: U N P A C K > > B U F F E R > > P A C K UNPACK >> BUFFER >> PACK UNPACK>>BUFFER>>PACK
类似于X2,相当于加了一个缓冲区,使得管道的输入和输出可以异步工作。 -
X5: C O P Y > > U N P A C K > > P A C K > > C O P Y COPY >> UNPACK >> PACK >> COPY COPY>>UNPACK>>PACK>>COPY
注意,这里 C O P Y COPY COPY是拷贝任意一个数据,不必是一个二进制位。这个管道类似于X4,相当于在左右添加一个容量为1的缓冲区,使得输入输出可以异步工作。 -
X6: C O P Y > > C O P Y COPY >> COPY COPY>>COPY
容量为2的缓冲区,最多在输出前预接受2个数据。
5.3 管道的操作规则
-
L1: P > > ( Q > > R ) = ( P > > Q ) > > R P>>(Q>>R) = (P>>Q)>>R P>>(Q>>R)=(P>>Q)>>R
管道满足结合律(因为最终总是要把内部全屏蔽完),但不满足交换律。 -
L2: ( r i g h t ! v → P ) > > ( l e f t ? y → Q ( y ) ) = P > > Q ( y ) (right!v \to P)>>(left?y \to Q(y))=P>>Q(y) (right!v→P)>>(left?y→Q(y))=P>>Q(y)
从 P P P出和从 Q Q Q进的动作在 P > > Q P>>Q P>>Q中对外屏蔽,但这一动作会影响 Q Q Q使其接下来执行 Q ( v ) Q(v) Q(v)。 -
L3: ( r i g h t ! v → P ) > > ( r i g h t ! w → Q ) = r i g h t ! w → ( ( r i g h t ! v → P ) > > Q ) (right!v \to P)>>(right!w \to Q)=right!w \to ((right!v \to P)>>Q) (right!v→P)>>(right!w→Q)=right!w→((right!v→P)>>Q)
从 P P P出和从 Q Q Q出的动作,其中前者(从 P P P出)是管道内部的动作,要在内部执行。 -
L4: ( l e f t ? x → P ( x ) ) > > ( l e f t ? y → Q ( y ) ) = l e f t ? x → ( P ( x ) > > ( l e f t ? y → Q ( y ) ) ) (left?x \to P(x))>>(left?y \to Q(y))=left?x \to (P(x)>>(left?y \to Q(y))) (left?x→P(x))>>(left?y→Q(y))=left?x→(P(x)>>(left?y→Q(y)))
从 P P P进和从 Q Q Q进的动作,其中后者(从 Q Q Q进)是管道内部的动作,要在内部执行。
5.4 管道的活锁(Livelock)现象
活锁是比递归程序出现 S T O P STOP STOP更坏的情况,其根本原因是管道屏蔽了内部动作,如:
P = ( r i g h t ! 1 → P ) Q = ( l e f t ? x → Q ) \begin{aligned} P & = (right!1 \to P) \\ Q & = (left?x \to Q) \end{aligned} PQ=(right!1→P)=(left?x→Q)
进程 P P P不断输出1,而进程 Q Q Q不断接受输入,两者连成管道 ( P > > Q ) (P>>Q) (P>>Q)后,从外部看来整个管道是静止的,其实内部在不停消耗计算资源。
这是一个最纯粹的活锁例子,这样的活锁现象会抢占正常工作的动作,如:
P = ( r i g h t ! 1 → P ∣ l e f t ? x → P 1 ( x ) ) Q = ( l e f t ? x → Q ∣ r i g h t ! 1 → Q 1 ) \begin{aligned} P & = (right!1 \to P \ | \ left?x \to P1(x)) \\ Q & = (left?x \to Q \ | \ right!1 \to Q1) \end{aligned} PQ=(right!1→P ∣ left?x→P1(x))=(left?x→Q ∣ right!1→Q1)
它们组成的管道 ( P > > Q ) (P>>Q) (P>>Q)会出现 P P P发送 Q Q Q接收的白白消耗计算资源的情况,则正常工作的部分( P P P接收、 Q Q Q发送)就被抢占了。
5.5 避免活锁(free of livelock)
如果进程 P P P不能无限的输出(而不受输入限制),那么就称 P P P是left-guarded的。其数学表达是:
∃ f ⋅ P s a t ( # r i g h t ≤ f ( l e f t ) ) \exists f\cdot P \ sat \ (\#right \leq f(left)) ∃f⋅P sat (#right≤f(left))
其中, # r i g h t \#right #right是指到任何时刻为止输出的数据长度。而 f f f是指一个函数,将到该时刻为止的输入映射到自然数集中。这是在要求任何时刻输出的数据长度都有一个上界,而这个上界取决于输入数据。例如"输入1个数据,随后输出10个该数据"这样的进程就是left-guarded,例如可以取到这样一个 f f f:
f ( l e f t ) = 11 × # l e f t f(left) = 11\times \#left f(left)=11×#left
从而总有 # r i g h t ≤ f ( l e f t ) \#right \leq f(left) #right≤f(left)即 10 t ≤ 11 t 10t \leq 11t 10t≤11t是成立的( t t t是经历的时刻)。
同理可以定义right-guarded,略。
- L1:如果任何用到 P P P的递归进程在 P P P左边都有guarded的输入,那么 P P P是left-guared的。
- L2:如果 P P P是left-guarded的,那么 ( P > > Q ) (P>>Q) (P>>Q)不会发生活锁。
- L3:如果 Q Q Q是right-guarded的,那么 ( P > > Q ) (P>>Q) (P>>Q)不会发生活锁。
这篇关于【进程代数学习笔记】4:[CSP]进程间的通道通信,管道与活锁避免的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









