算法通关村第三关—继续讨论数据问题(黄金)

本文主要是介绍算法通关村第三关—继续讨论数据问题(黄金)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

继续讨论数据问题

一、数组中出现次数超过一半的数字

Leetcode 169.多数元素数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如：输入如下所示的一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2(题目保证出现该数)
剑指offer中的类似题目条件增加：如果该数不存在，则输出0。
首先，用排序行不行？这里说一定存在出现次数超过一半的数字了，那么先对数组进行排序。在一个有序数组中次数超过一半的必定是中位数，所以可以直接取出中位数。如果不放心，可以再遍历数组，确认一下这个数字是否出现次数超过一半。OK,没问题，第一种方法就出来了。这种方法的的时间复杂度取决于排序算法的时间复杂度，最快为O(logn)。由于排序的代价比较高，所以我们继续找其他方法。

//按leetcode要求写的，返回0的情况没写
class Solution {public int majorityElement(int[] nums) {Arrays.sort(nums);return nums[nums.length / 2];}
}

其次，用Hash行不行？我们先创建一个HashMap的key是元素的值，value是已经出现的次数，然后遍历数组来统计所有元素出现的次数。最后再次遍历Hash,找到出现次数超过一半的数字。OK,第二种方法出来了，代码就是：

public int moreThanHalfNum(int[] array){if(array == null) return 0;Map<Integer,Integer> res = new HashMap<>();int len = array.length;for(int i = 0; i < array.length; i++){res.put(array[i], res.getorDefault(array [i],0) + 1);if(res.get(array[i]) > len / 2) return array[i];}return 0;
}

二、数组中只出现一次的数字

LeetCode136.给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次，找出那个只出现了一次的元素。

这个题貌似使用Set集合比较好，Set集合不存重复值，这一特点可以利用。题目明确说其他元素都是出现两次，我们也可以利用这个操作，当要添加的元素key与集合中已存在的数重复时，不再进行添加操作，而是将集合中的key一起删掉，这样整个数组遍历完后，集合中就只剩下了那个只出现了一次的数字了。

class Solution {public int singleNumber(int[] nums) {Set<Integer> set = new HashSet();for(int num : nums){//if(set.contains(num))写成这样也行if(!set.add(num)){set.remove(num);}else set.add(num);}for(int num : set) return num;return 0;}
}

上面要注意，必须存在那个只出现了一次的数字，否则St集合长度将为0，最后一行代码运行时会出错。
第二种方法：位运算这个题面试官可能还会让你用位运算来做，该怎么办呢？
异或运算的几个规则是：

0与其他数字异或的结果是那个数字，相等的数字异或得0。要操作的数组中除了某个数字只出现了一次之外，其他数字都出现了两次，所以可以定义一个变量赋初始值为0，用这个变量与数组中每个数字做异或运算，并将这个变量值更新为那个运算结果，直到数组遍历完毕，最后得到的变量的值就是数组中只出现了一次的数字了。这种方法只需遍历一次数组即可，代码如下：

class Solution {public int singleNumber(int[] nums) {int num = 0;for(int num1 : nums){num ^= num1;}return num;}
}

颜色分类问题(荷兰国旗问题)

我们使用整数0、1和2分别表示红色、白色和蓝色。必须在不使用库的sort函数的情况下解决这个问题。

这个题是非常经典的双指针问题，而且还可以使用多种方式的双指针。这里我们分析两种方法，一种与冒泡排序非常类似，一种与快速排序非常类似。

1.基于冒泡排序的双指针（快慢指针）

冒泡排序我们都知道，就是根据大小逐步和后面的比较，慢慢调整到整体有序。这种方法还是稳定的排序方法。
我们可以考虑对数组进行两次遍历。在第一次遍历，我们将数组中所有的0交换到数组的头部，这样第二次遍历只需要处理1和2的问题就行了，而这两次寻找本身又是非常漂亮的双指针。代码如下：

public void sortColors(int[] nums){int n = nums.length;int left = 0;//将所有的0交换到数组的最前面，第一次快慢指针for(int right = 0; right < n; right++){if(nums[right] == 0){int temp = nums [right];nums[right] = nums [left];nums[left] = temp;left++;}}//将所有的1交换到2的前面，第二次快慢指针for(int right = left; right < n; right++){if(nums[right] == 1){int temp = nums[right];nums[right] = nums[left];nums[left] = temp;left++;}}
}

上面的方式能解决问题，而且效率还不错。但是面试官可能又给你出幺蛾子，能否将两次遍历变成一次搞定？

2.三指针

我们要使用三个指针才行：
·Ieft指针，表示left左侧的元素都是0
·right指针，表示right右侧的元素都是2
·index指针，从头到尾遍历数组，根据nums[index]是0还是2决定与left交换还是与right交换。
index位置上的数字代表着我们当前需要处理的数字。当index为数字1的时候，我们什么都不需要做，直接+1即可。如果是0，我们放到左边，如果是2，放到右边。如果index=right,则可以停止。我们看一下图示：

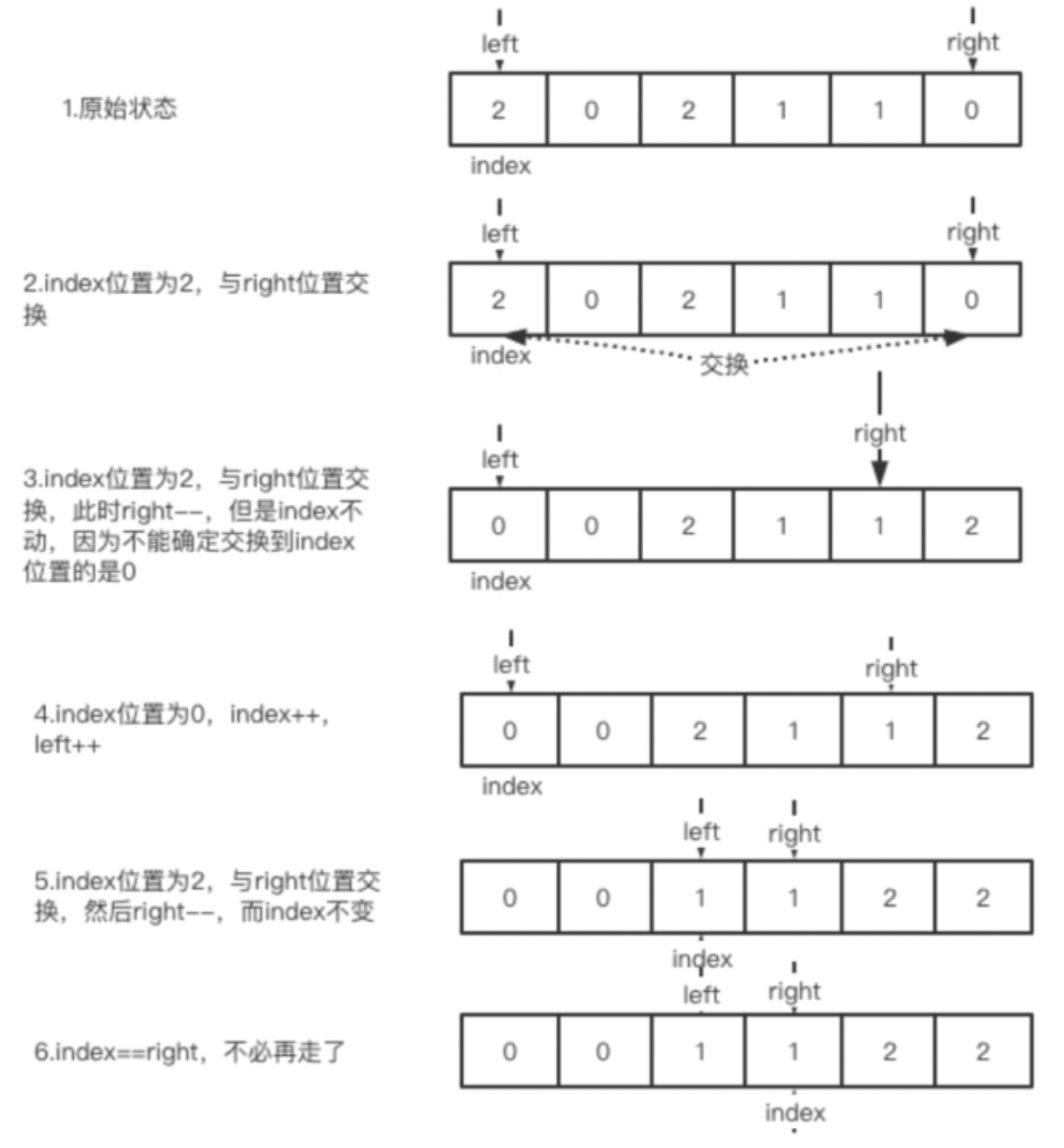
这里的重点和难点index位置为2进行交换后为什么只进行right.–,而不用index±+呢？这是因为我们right位置交换过来的元素可能是0，也可能是1。如果是0自然没问题，但是如果是1则执行index++就将1跳过无法处理了。所以我们先不动index,在下一次循环时继续判断这个index位置元素是不是0。
那为啥index位置是0的时候执行swap就可以index++了呢，这是因为如果index前面位置如果存在位置都会被swap到right位置去了，这里只需要处理0和1的情况就可以了。
代码如下：

public void sortColors(int[] nums){int left = 0, right = nums.length - 1;int index = 0;while(index <= right){if (nums[index] == 0)swap(nums,  index++, left++);else if(nums [index ]== 2)swap(nums,index,right--);else index++;}
}
private void swap(int[]nums,int i,int j){int temp=nums [i];nums [i]=nums [j];nums [j]=temp;
}

3.哈希表

自己尝试做这道题的时候，首先想到用哈希表的方法，统计0，1，2的个数，然后三次循环给数组赋值

class Solution {public void sortColors(int[] nums) {// if(nums.length == 0) return;// Map<Integer, Integer> map = new HashMap();// map.put(0,0);map.put(1,0);map.put(2,0);// for(int i = 0; i < nums.length; i++){//     map.put(nums[i],map.get(nums[i]) + 1);// }// for(int i = 0; i < map.get(0); i++) nums[i] = 0;// for(int i = map.get(0); i < map.get(0) + map.get(1); i++) nums[i] = 1;// for(int i = map.get(0) + map.get(1); i < nums.length; i++) nums[i] = 2;int n = nums.length;int left = 0;//将所有的0交换到数组的最前面for(int right = 0; right < n; right++){if(nums[right] == 0){int temp = nums [right];nums[right] = nums [left];nums[left] = temp;left++;}}//将所有的1交换到2的前面for(int right = left; right < n; right++){if(nums[right] == 1){int temp = nums[right];nums[right] = nums[left];nums[left] = temp;left++;}}}
}