本文主要是介绍2020 Multi-University Training Contest #1 1010 Math is Simple,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2020 Multi-University Training Contest #1 1010 Math is Simple
题意
hdu-6760 Math is Simple
给定一个n,求解如下式子
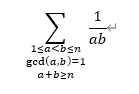
题解
设a+b=n时,设 g ( n ) = ∑ a = 1 n 1 a ( n − a ) [ g c d ( a , n − a ) = = 1 ] [ a < n − a ] g(n)=\sum_{a=1}^n\frac{1}{a(n-a)}[gcd(a,n-a)==1][a<n-a] g(n)=∑a=1na(n−a)1[gcd(a,n−a)==1][a<n−a], 1 a ( n − a ) = 1 n ( 1 a + 1 n − a ) \frac{1}{a(n-a)}=\frac{1}{n}(\frac{1}{a}+\frac{1}{n-a}) a(n−a)1=n1(a1+n−a1)。
由对称型可得 g ( n ) = 1 n ( ∑ a = 1 n 1 a [ g c d ( a , n ) = = 1 ] ) g(n)=\frac{1}{n}(\sum_{a=1}^n\frac{1}{a}[gcd(a,n)==1]) g(n)=n1(∑a=1na1[gcd(a,n)==1])
通过反演再推导出 g ( n ) = 1 n ∑ d ∣ n μ ( d ) 1 d ∑ i = 1 n d 1 i g(n)=\frac{1}{n}\sum_{d|n}\mu(d)\frac{1}{d}\sum_{i=1}^{\frac{n}{d}} \frac{1}{i} g(n)=n1∑d∣nμ(d)d1∑i=1dni1
通过前缀和处理出 ∑ i = 1 n d 1 i \sum_{i=1}^{\frac{n}{d}} \frac{1}{i} ∑i=1dni1
f ( n ) − f ( n − 1 ) = g ( n ) − g ( n − 1 ) f(n)-f(n-1)=g(n)-g(n-1) f(n)−f(n−1)=g(n)−g(n−1)
f ( n ) − f ( 2 ) = g ( n ) − g ( 2 ) f(n)-f(2)=g(n)-g(2) f(n)−f(2)=g(n)−g(2),
f ( n ) = g ( n ) + 1 2 f(n)=g(n)+\frac{1}{2} f(n)=g(n)+21
然后就可以枚举n的因数对 g ( n ) g(n) g(n)进行求解。(卡了预处理 μ ( n ) \mu(n) μ(n)的常数)
代码
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define N 100000000
#define M 11000
#define mod 998244353
#define inv2 499122177
inline int powmod(int a, int b) {int res = 1;a = a % mod;while(b) {if(b & 1) res = (ll)res * a % mod;a = (ll)a * a % mod;b >>= 1;}return res;
}
int inv[N + 5];
void init() {inv[1] = 1;for(int i = 2; i <= N; i++) {inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;}for(int i = 2; i <= N; i++) {inv[i] = (inv[i] + inv[i - 1]) % mod;}
}
int v[50], top;
int res, n;
void dfs(int id, int d, int mu) {if(id == top + 1) {mu = (mu + mod) % mod;res = (res + (ll)mu * (inv[d] - inv[d - 1] + mod) % mod * inv[n / d] % mod) % mod;return; }dfs(id + 1, d, mu);dfs(id + 1, d * v[id], -mu);
}
int main() {init();int t;scanf("%d", &t);while(t--) {scanf("%d", &n);if(n == 2) {printf("%d\n", inv2);continue;}int y = n;top = 0;ll invn = powmod(n, mod - 2);for(int i = 2; i * i <= n; i++) {if(n % i == 0) {v[++top] = i;while(n % i == 0) {n /= i;}}}if(n != 1) {v[++top] = n;}n = y;res = 0;dfs(1, 1, 1);res = (1ll * res * invn % mod + inv2) % mod;printf("%lld\n", res);}
}这篇关于2020 Multi-University Training Contest #1 1010 Math is Simple的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





