贝叶斯思维——chapter4(估计进阶)

本文主要是介绍贝叶斯思维——chapter4(估计进阶)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

贝叶斯思维——chapter4(估计进阶)

写在前面：
库文件链接：thinkbayes.py

4.1 欧元问题

问题：

《信息论：推理和学习算法》中，有过这样一个问题：“当硬币以边缘转动250次,得到正面140次，反面110次。”，“统计学声明称：如果这是一个均匀的硬币，这样的结果出现的可能性小于7%。”

上述结果是否对“硬币偏心而非均匀”提供了证据？

解：

我们将采取一下步骤来回答这个问题。

估计该硬币正面朝上的概率。
估计该数是否支持硬币偏心的假设。

已知一个硬币，那么我们以其边缘转动，它正面朝上的概率都是确定的x。（取决于硬币的物理特性——重量分布）
如果硬币的重量分布是均匀的，那么我们认为这里的x接近50%，但是作为一个不均匀的硬币，这个x应该会有较大差别。
我们接下来要利用贝叶斯定理和观察到的数据来估计x。
我们先定义假设 $H_x$ ，表示正面朝上的概率为x％:

hypos = range(1,101)

说先从均匀的先验概率开始。后面我们在考虑其他的先验概率。
likelihood的函数相对容易，若 $H_x$ 为真，正面朝上概率为x/100，反面朝上概率为(1 - x/100)。

class Euro(Suite):def __init__(self, hypos):pass#可以参考上一篇def likelihood(self, data, hypo):x = hypoif data == 'H'return x/100.0return 1 - x/100.0def Update(self,data):pass#可以参考上一篇

利用观察到的数据对x进行估计。

suite  = Euro(hypos)
dataSet = 'H'*140+'T'*110
for data in dataSet:suite.Update(data)

总结：在均匀分布的先验概率前提下，后验分布会有一个较为明显的偏移。

4.2 后验概率的概述

总结一下，有几种方式来概括后验概率分布的特征。

找后验概率的最大似然。（你会发现这里的最大似然实际上就等于观察得到的百分比140/250）
计算平均数和中位数来概述后验概率。
计算置信区间来概述后验概率。

回到原来的问题，我们想知道硬币是否是均匀的。当观察到的后验可信区间不包括50％，我们认为硬币的重量分布的确是不均匀的。
但确切地说，这不是我们最开始的问题。之前的问题是“这些数据是否恰恰为——硬币偏心而非均匀——给出了证据？要回答这个问题，我们需要更加精确得理解‘数据为某假说提供证据’这句化的含义，这个放到下一章讲”。
既然我们想要知道硬币是否是均匀的，很自然得想到是求x为50%的概率：

suite.Prob(50)
>>>0.021

然而这个值几乎不能说明什么，这使得对假设的评估显得毫无意义。我们可以通过将范围区间划分为更多或者更少的细小区间。这样，对给定的假设的概率会更大或更小。

4.3 先验概率的湮没

我们之前假设先验是均匀的，但这可能不是一个好的假设。如果硬币是偏心的，我们可以相信x会大幅度偏离50％，但如果偏心到10%或者90%就近乎不可能。
更合理的方式，是为50%附近给出一个相对与10%或者90%更高的先验概率。
我们可以构建一个三角先验分布的例子：
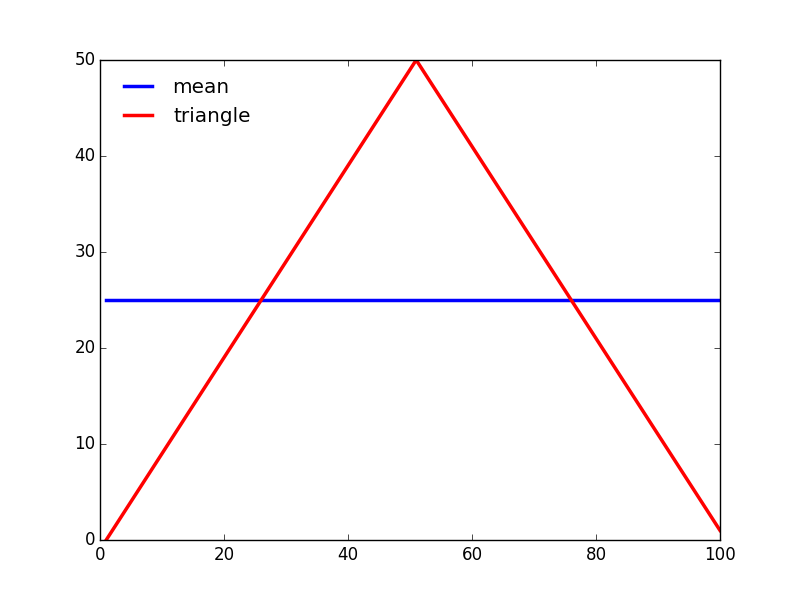
此处输入图片的描述
只是给力一个先验分布的形状，还需要做归一化。
下面的代码构成了所谓的三角先验分布：

 def TrianglePrior():suite = Eurofor x in range(0,51):suite.Set(x,x)for x in range(51,101):suite.Set(x,100-x);suite.Normalize()

事实上，即使我们应用了不同的先验，后验分布也非常得相似。
这就是先验湮没的一个例子：如果有足够的数据，计时在先验分布上持有不同的观点，我们也会得到趋于收敛的后验概率。

4.4 优化

从上述的代码我们可以看到，对于每个得到的数据我们都会单独的应用一次Update,从上一章的Update的实现中我们可以看到在每次应用一次该函数，都需要进行一次归一化处理。
所以，如果我们已知了一个数据的序列，就没有必要一个一个得进行训练，对所有数据都训练结束了，再进行归一化即可。

def UpdateSet(self, dataSet):for data in dataSet:for hypo in self.Values():like = self.Likelihood(data, hypo)self.Mult(hypo, like)return self.Normalize()

这样处理会在一定程度上优化我们的速度，但time依然与数据量成正比。我们可以通过改写Likelihood来处理整个数据集，而不是一次模拟运行一次。
对于之前的硬币版本改动如下：

def Likelihood(self, data, hypo):x = hypo/100.0heads, tails = datalike = x**heads * (1 - x)**tailsreturn like

然后我们就可以用两个整数的元组来调用Update:

heads, tails = 140, 110
suite.Update((heads, tails))

我们用指数函数的计算取代了原来的乘法，这样对于任意次数的硬币模拟消耗的运行时间基本一致。

4.5 Beta分布

还有一个优化可以让解法更快。
到目前位置，我们的假设都是取的一组离散值。现在，我们将使用一个连续分布，确切得说，应该是beta分布。

f (x; α, β) = Γ ( α + β ) Γ ( α ) Γ ( β ) x α - 1 (1 - x) β - 1 beta 分 布 f (x; α, β) \propto x α - 1 (1 - x) β - 1 Γ (α) = \int \infty 0 t α - 1 e - t d t gamma 分 布

$f(x;\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\qquad \text{beta 分布}\\ f(x;\alpha,\beta) \propto x^{\alpha-1}(1-x)^{\beta-1}\\ \Gamma(\alpha) = \int_0^{\infty}t^{\alpha-1}e^{-t}\,dt\qquad \text{gamma 分布}$
这时候我们可以做积分变化

t=βx $t = \beta x$ ,可得：

Γ (α, β) = β α \int \infty 0 x α - 1 e - x β d x, 从 而 1 Γ ( α , β ) β α \int \infty 0 x α - 1 e - x β d x = 1

$\Gamma(\alpha,\beta)=\beta^{\alpha}\int_0^\infty x^{\alpha-1}e^{-x\beta}dx,\text{从而}\\ \frac{1}{\Gamma(\alpha,\beta)}\beta^{\alpha}\int_0^\infty x^{\alpha-1}e^{-x\beta}dx=1$
beta分布定义在从0到1的闭区间上，用一句话来说，beta分布可以看做是一个概率的概率分布，当你不知道一个事件发生的概率是多少时，beta分布给出了所有概率的出现的可能性的大小。
我们令：

1 B ( α , β ) = Γ ( α + β ) Γ ( α ) Γ ( β )

$\frac{1}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$
这里的B函数是一个标准化函数，它只是为了使得这个分布的概率密度积分等于1才加上的。

二项分布的似然函数

p (y | x) = C k n x k (1 - x) (n - k) \propto x k (1 - x) (n - k)

$p(y|x)=C_n^k x^k(1-x)^{(n-k)} \propto x^k(1-x)^{(n-k)}$

贝叶斯估计

我们做贝叶斯估计的目的就是要在给定y的情况下求出x,所以我们的目的是求解如下的后验概率：

P (x | y) = P ( y | x ) P ( x ) P ( y ) \propto P (y | x) P (x)

$P(x|y)=\frac{P(y|x)P(x)}{P(y)}\propto P(y|x)P(x)$
注意，这里因为

P(y) $P(y)$ 与我们所要估计的

x $x$ 是独立的，因此我们可以不考虑它。

共轭先验

现在我们有了二项分布的似然函数和beta分布，现在我们要将beta分布代入到贝叶斯估计的 $P(x)$ 中，将二项分布的似然函数代入到 $P(y|x)$ 中，可以得到：

P (x | y) \propto x k (1 - x) (n - k) * x α - 1 (1 - x) β - 1 \propto x (α + k - 1) (1 - x) (n + β - k - 1) (1) (2)

$\begin{align} P(x|y) & \propto x^k(1-x)^{(n-k)}*x^{\alpha-1}(1-x)^{\beta-1} \tag 1\\ & \propto x^{(\alpha + k - 1)}(1-x)^{(n+\beta-k-1)} \tag 2\\ \end{align}$
我们假设

a′=a+k,b′=n+β−k $a\prime = a+k,b\prime = n+\beta-k$
最后我们发现这个贝叶斯估计服从

beta(a′,b′) $beta(a\prime,b\prime)$ 分布的，我们只要用B函数将它标准化就得到我们的后验概率：

p (x | y) = 1 B ( a ' , b ' ) x (a' - 1) (1 - x) (b' - 1)

$p(x|y)=\frac{1}{B(a\prime,b\prime)}x^{(a\prime-1)}(1-x)^{(b\prime-1)}$
这相当于如果我们的先验概率是带有参数的a,b的beta分布，我们看到h次正面和t次反面的数据，后验概率就是参数为a+h,b+t的beta分布。换句话来说，我们通过两个假发就实现了Update方法。
这样的处理会大大简化我们的计算，只不过仅试用与先验概率的分布的确是bets分布的情况。幸运的是，在最低限度上，对许多实际的先验分布beta分布都可以进行良好的近似，同时也可以完美匹配均匀先验。参数a = 1和b = 1的beta分布就是从0到1的均匀分布。
thinkbayes.py提供了一个类来表示beta分布：

class Beta(object):def __init__(self, alpha = 1, beta = 1):self.alpha = alphaself.beta = beta

默认情况下，__init__使用均匀分布。Update进行贝叶斯更新：

    def Update(self, data):heads, tails = dataself.alpha += headsself.beta += tails

data是一对表示正面和反面的数量的整数。
因此，我们的得到了另一种解决欧元问题的方法：

beta = thinkbayes.Beta()
beta.Update((140, 110))
print beta.Mean()

beta提供了Mean，计算期望的函数：

    def Mean(self):return float(self.alpha) / (self.alpha + self.beta)

4.6 讨论

我们可以看到，在较大数据集的情况下，先验之间的区别被掩盖了，这会减轻一些我们在前面一张关于客观性的担忧。甚至很对现实世界的问题，明显不同的先验概率最终会被矫正。
但事实并不总是如此。首先，请记住，所有贝叶斯分析是基于模型决策的。如果两个人没有选择相同的模型，我们可能对数据进行不同的解读。因此，即使使用相同的数据，我们也可能得到不同的似然度，因而后验概率可能不会收敛。
另外，请注意，在贝叶斯Update中，我们以一个似然度乘以每个先验概率，所以如果p(H)为0，则p(H|D)也为0。在欧元问题上，如果我们确定x小于50%，并指定大于50%的假设概率都为0，那么再多的数据都无法说服你。
这种看法是克伦威尔法则的基础，建议是：应当避免设置任何一个假设的先验概率为0，哪怕的确存在这种可能性。

这篇关于贝叶斯思维——chapter4(估计进阶)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！