JavaScript ＜关于逆向RSA非对称加密算法的案例(附原代码)＞--案例(五)

本文主要是介绍JavaScript ＜关于逆向RSA非对称加密算法的案例(附原代码)＞--案例(五)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言:

趁热打铁,标记一下RSA的算法逆向...第二篇会有详解(本篇重在过程)

正文:

废话不说,直接分析步骤图:

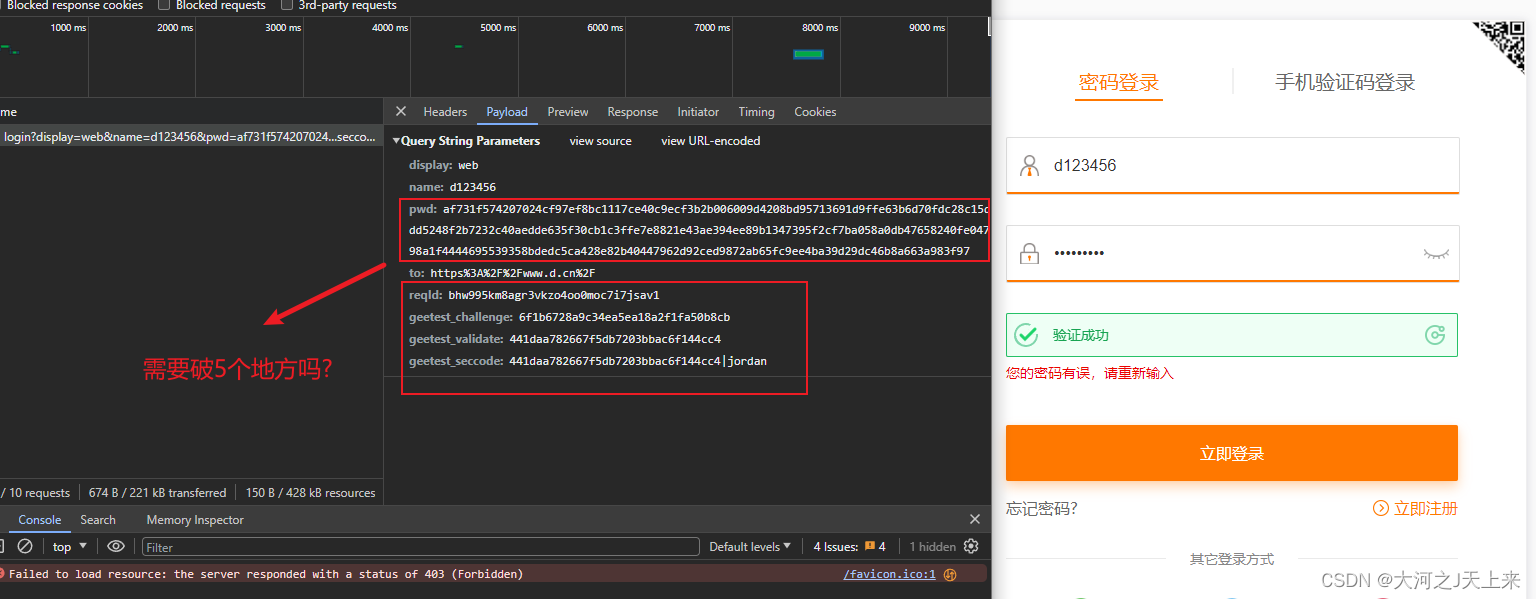
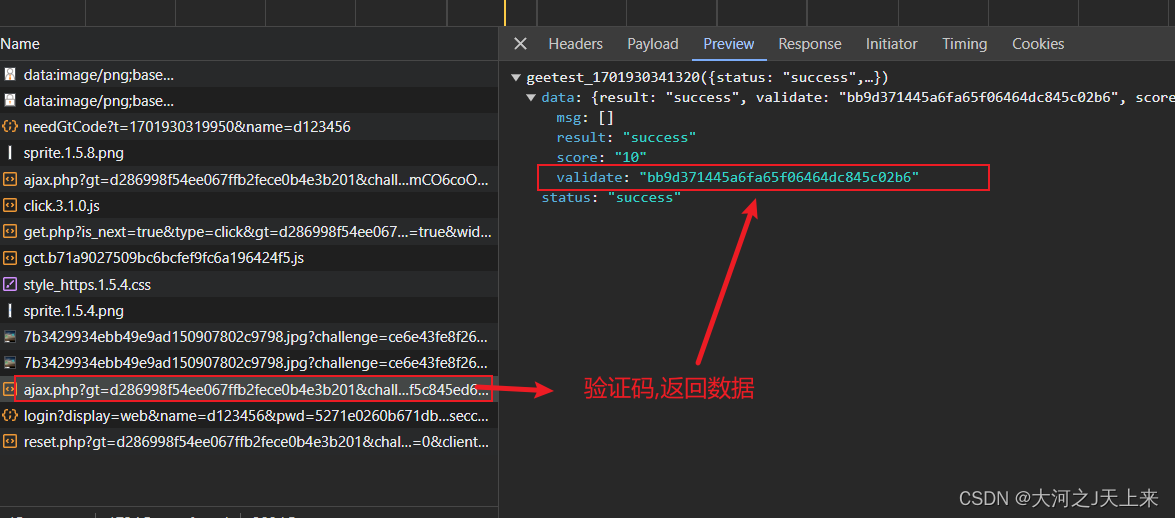
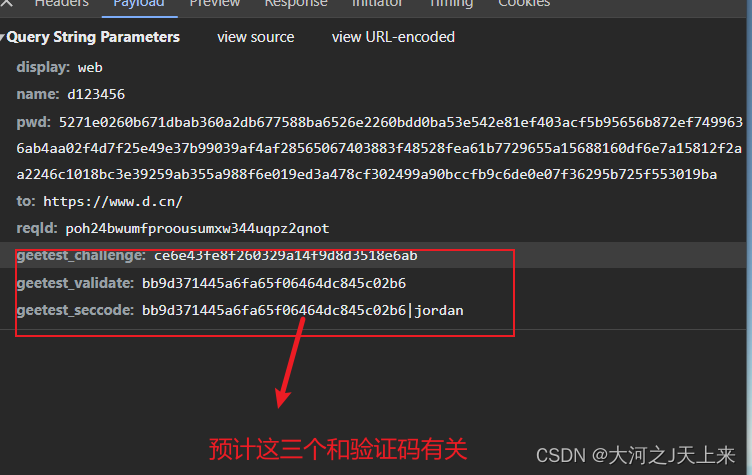
到了这里,可以看到在登录的时候,需要验证码(本篇不教反验证码)

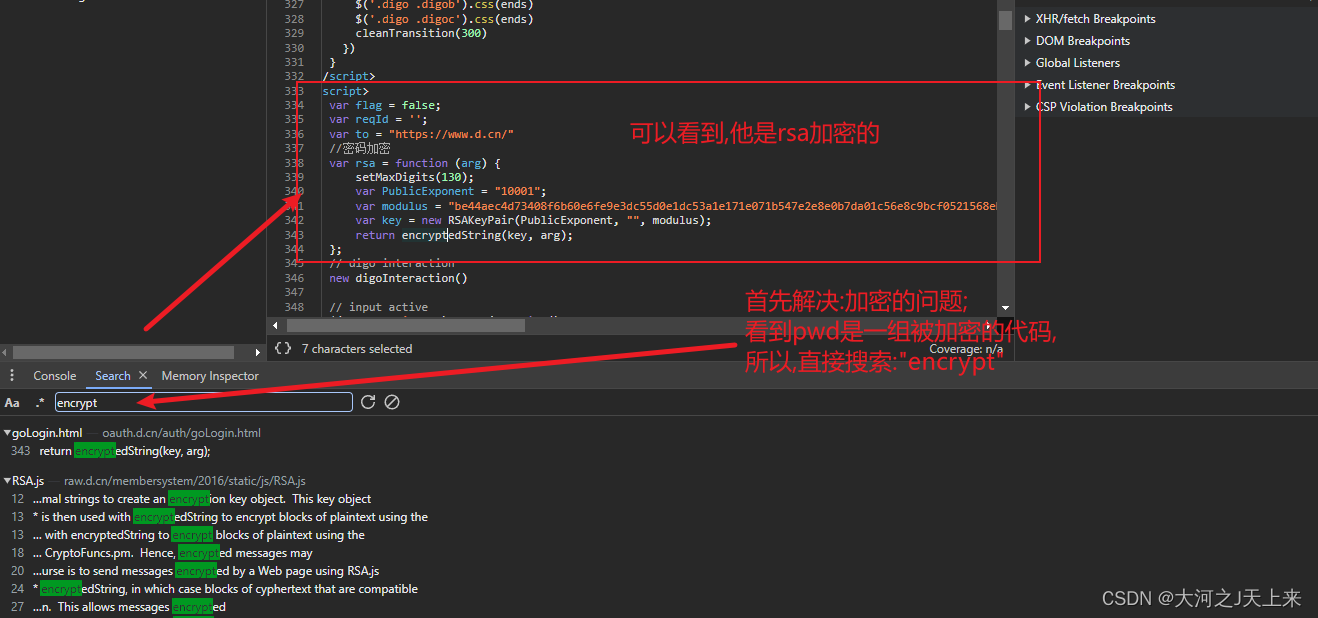
下面是正题--->逆他的pwd(密码)

---

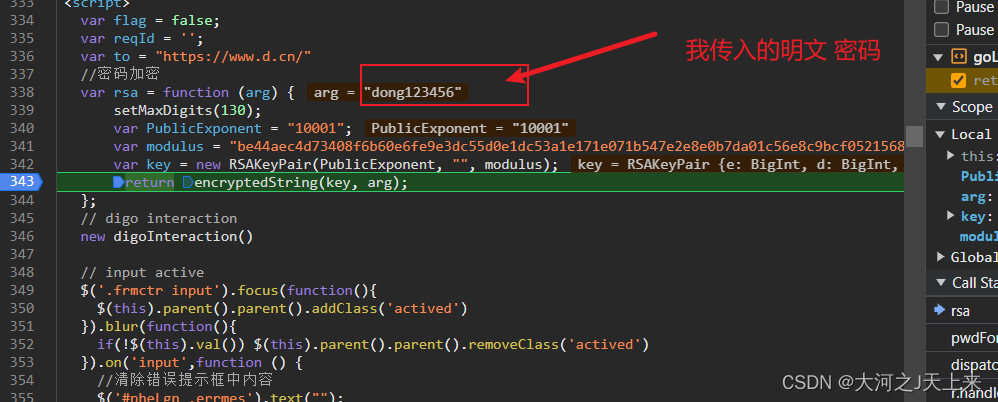
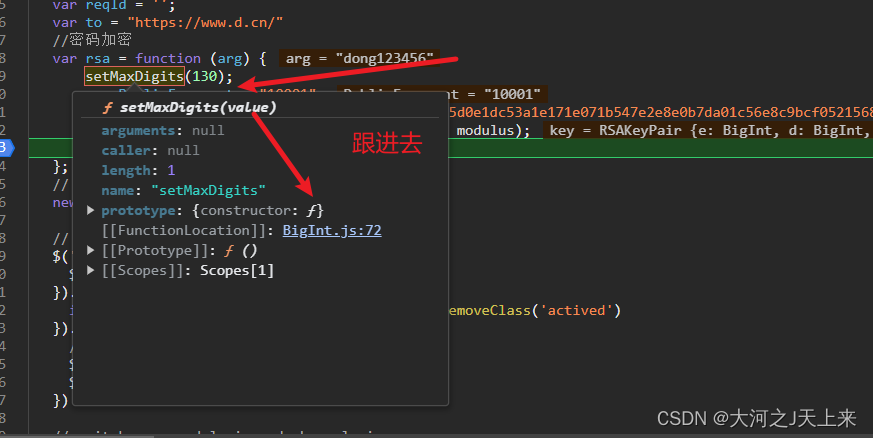
总结:

问题:怎么确定一个密文数据是基于什么算法做出来的呢?

答: 1.看他是由什么组成的

•         --如果光是由 '字母和数字'组成
•                 --由字母和数字组成的32位密文数据 ,MD5
•                 --由字母和数字组成的64位密文数据 ,SHA-256(生成256位长度的哈希值，这通常以64个十六进制字符呈现)
•                 --由字母和数字组成的256位密文数据,RSA 
•         ---以上是通常的例子

针对rsa,直接抠他代码会比较直接,但是比较繁琐; 当你过了一遍他的代码,没大问题,一样可以引用crypto库进行解密

全篇js代码:

var bitsPerDigit=16
function arrayCopy(src, srcStart, dest, destStart, n)
{var m = Math.min(srcStart + n, src.length);for (var i = srcStart, j = destStart; i < m; ++i, ++j) {dest[j] = src[i];}
}
var maxDigitVal = 65535
var biRadixBits =16
function biMultiplyDigit(x, y)
{var n, c, uv;result = new BigInt();n = biHighIndex(x);c = 0;for (var j = 0; j <= n; ++j) {uv = result.digits[j] + x.digits[j] * y + c;result.digits[j] = uv & maxDigitVal;c = uv >>> biRadixBits;}result.digits[1 + n] = c;return result;
}function biNumBits(x)
{var n = biHighIndex(x);var d = x.digits[n];var m = (n + 1) * bitsPerDigit;var result;for (result = m; result > m - bitsPerDigit; --result) {if ((d & 0x8000) != 0) break;d <<= 1;}return result;
}
var highBitMasks = new Array(0x0000, 0x8000, 0xC000, 0xE000, 0xF000, 0xF800,0xFC00, 0xFE00, 0xFF00, 0xFF80, 0xFFC0, 0xFFE0,0xFFF0, 0xFFF8, 0xFFFC, 0xFFFE, 0xFFFF);
function biShiftLeft(x, n)
{var maxDigitVal= 65535var digitCount = Math.floor(n / bitsPerDigit);var result = new BigInt();arrayCopy(x.digits, 0, result.digits, digitCount,result.digits.length - digitCount);var bits = n % bitsPerDigit;var rightBits = bitsPerDigit - bits;for (var i = result.digits.length - 1, i1 = i - 1; i > 0; --i, --i1) {result.digits[i] = ((result.digits[i] << bits) & maxDigitVal) |((result.digits[i1] & highBitMasks[bits]) >>>(rightBits));}result.digits[0] = ((result.digits[i] << bits) & maxDigitVal);result.isNeg = x.isNeg;return result;
}
function biMultiplyByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, 0, result.digits, n, result.digits.length - n);return result;
}
function biCompare(x, y)
{if (x.isNeg != y.isNeg) {return 1 - 2 * Number(x.isNeg);}for (var i = x.digits.length - 1; i >= 0; --i) {if (x.digits[i] != y.digits[i]) {if (x.isNeg) {return 1 - 2 * Number(x.digits[i] > y.digits[i]);} else {return 1 - 2 * Number(x.digits[i] < y.digits[i]);}}}return 0;
}
function biSubtract(x, y)
{var result;if (x.isNeg != y.isNeg) {y.isNeg = !y.isNeg;result = biAdd(x, y);y.isNeg = !y.isNeg;} else {result = new BigInt();var n, c;c = 0;for (var i = 0; i < x.digits.length; ++i) {n = x.digits[i] - y.digits[i] + c;result.digits[i] = n & 0xffff;// Stupid non-conforming modulus operation.if (result.digits[i] < 0) result.digits[i] += biRadix;c = 0 - Number(n < 0);}// Fix up the negative sign, if any.if (c == -1) {c = 0;for (var i = 0; i < x.digits.length; ++i) {n = 0 - result.digits[i] + c;result.digits[i] = n & 0xffff;// Stupid non-conforming modulus operation.if (result.digits[i] < 0) result.digits[i] += biRadix;c = 0 - Number(n < 0);}// Result is opposite sign of arguments.result.isNeg = !x.isNeg;} else {// Result is same sign.result.isNeg = x.isNeg;}}return result;
}
var lowBitMasks = new Array(0x0000, 0x0001, 0x0003, 0x0007, 0x000F, 0x001F,0x003F, 0x007F, 0x00FF, 0x01FF, 0x03FF, 0x07FF,0x0FFF, 0x1FFF, 0x3FFF, 0x7FFF, 0xFFFF);
function biShiftRight(x, n)
{var digitCount = Math.floor(n / bitsPerDigit);var result = new BigInt();arrayCopy(x.digits, digitCount, result.digits, 0,x.digits.length - digitCount);var bits = n % bitsPerDigit;var leftBits = bitsPerDigit - bits;for (var i = 0, i1 = i + 1; i < result.digits.length - 1; ++i, ++i1) {result.digits[i] = (result.digits[i] >>> bits) |((result.digits[i1] & lowBitMasks[bits]) << leftBits);}result.digits[result.digits.length - 1] >>>= bits;result.isNeg = x.isNeg;return result;
}
function biDivideModulo(x, y)
{var nb = biNumBits(x);var tb = biNumBits(y);var origYIsNeg = y.isNeg;var q, r;if (nb < tb) {// |x| < |y|if (x.isNeg) {q = biCopy(bigOne);q.isNeg = !y.isNeg;x.isNeg = false;y.isNeg = false;r = biSubtract(y, x);// Restore signs, 'cause they're references.x.isNeg = true;y.isNeg = origYIsNeg;} else {q = new BigInt();r = biCopy(x);}return new Array(q, r);}q = new BigInt();r = x;var bitsPerDigit =16// Normalize Y.var t = Math.ceil(tb / bitsPerDigit) - 1;var lambda = 0;var biHalfRadix= 32768while (y.digits[t] < biHalfRadix) {y = biShiftLeft(y, 1);++lambda;++tb;t = Math.ceil(tb / bitsPerDigit) - 1;}// Shift r over to keep the quotient constant. We'll shift the// remainder back at the end.r = biShiftLeft(r, lambda);nb += lambda; // Update the bit count for x.var n = Math.ceil(nb / bitsPerDigit) - 1;var b = biMultiplyByRadixPower(y, n - t);while (biCompare(r, b) != -1) {++q.digits[n - t];r = biSubtract(r, b);}for (var i = n; i > t; --i) {var ri = (i >= r.digits.length) ? 0 : r.digits[i];var ri1 = (i - 1 >= r.digits.length) ? 0 : r.digits[i - 1];var ri2 = (i - 2 >= r.digits.length) ? 0 : r.digits[i - 2];var yt = (t >= y.digits.length) ? 0 : y.digits[t];var biRadix = 65536var yt1 = (t - 1 >= y.digits.length) ? 0 : y.digits[t - 1];if (ri == yt) {q.digits[i - t - 1] = maxDigitVal;} else {q.digits[i - t - 1] = Math.floor((ri * biRadix + ri1) / yt);}var biRadixSquared =4294967296var c1 = q.digits[i - t - 1] * ((yt * biRadix) + yt1);var c2 = (ri * biRadixSquared) + ((ri1 * biRadix) + ri2);while (c1 > c2) {--q.digits[i - t - 1];c1 = q.digits[i - t - 1] * ((yt * biRadix) | yt1);c2 = (ri * biRadix * biRadix) + ((ri1 * biRadix) + ri2);}b = biMultiplyByRadixPower(y, i - t - 1);r = biSubtract(r, biMultiplyDigit(b, q.digits[i - t - 1]));if (r.isNeg) {r = biAdd(r, b);--q.digits[i - t - 1];}}r = biShiftRight(r, lambda);// Fiddle with the signs and stuff to make sure that 0 <= r < y.q.isNeg = x.isNeg != origYIsNeg;if (x.isNeg) {if (origYIsNeg) {q = biAdd(q, bigOne);} else {q = biSubtract(q, bigOne);}y = biShiftRight(y, lambda);r = biSubtract(y, r);}// Check for the unbelievably stupid degenerate case of r == -0.if (r.digits[0] == 0 && biHighIndex(r) == 0) r.isNeg = false;return new Array(q, r);
}
function biDivide(x, y)
{return biDivideModulo(x, y)[0];
}
function biCopy(bi)
{var result = new BigInt(true);result.digits = bi.digits.slice(0);result.isNeg = bi.isNeg;return result;
}
function biDivideByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, n, result.digits, 0, result.digits.length - n);return result;
}
function biModuloByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, 0, result.digits, 0, n);return result;
}
function BarrettMu_modulo(x)
{var q1 = biDivideByRadixPower(x, this.k - 1);var q2 = biMultiply(q1, this.mu);var q3 = biDivideByRadixPower(q2, this.k + 1);var r1 = biModuloByRadixPower(x, this.k + 1);var r2term = biMultiply(q3, this.modulus);var r2 = biModuloByRadixPower(r2term, this.k + 1);var r = biSubtract(r1, r2);if (r.isNeg) {r = biAdd(r, this.bkplus1);}var rgtem = biCompare(r, this.modulus) >= 0;while (rgtem) {r = biSubtract(r, this.modulus);rgtem = biCompare(r, this.modulus) >= 0;}return r;
}
function biMultiply(x, y)
{var result = new BigInt();var c;var n = biHighIndex(x);var t = biHighIndex(y);var u, uv, k;for (var i = 0; i <= t; ++i) {c = 0;k = i;for (j = 0; j <= n; ++j, ++k) {uv = result.digits[k] + x.digits[j] * y.digits[i] + c;result.digits[k] = uv & maxDigitVal;c = uv >>> biRadixBits;}result.digits[i + n + 1] = c;}// Someone give me a logical xor, please.result.isNeg = x.isNeg != y.isNeg;return result;
}
function BarrettMu_multiplyMod(x, y)
{/*x = this.modulo(x);y = this.modulo(y);*/var xy = biMultiply(x, y);return this.modulo(xy);
}function BarrettMu_powMod(x, y)
{var result = new BigInt();result.digits[0] = 1;var a = x;var k = y;while (true) {if ((k.digits[0] & 1) != 0) result = this.multiplyMod(result, a);k = biShiftRight(k, 1);if (k.digits[0] == 0 && biHighIndex(k) == 0) break;a = this.multiplyMod(a, a);}return result;
}function BarrettMu(m)
{this.modulus = biCopy(m);this.k = biHighIndex(this.modulus) + 1;var b2k = new BigInt();b2k.digits[2 * this.k] = 1; // b2k = b^(2k)this.mu = biDivide(b2k, this.modulus);this.bkplus1 = new BigInt();this.bkplus1.digits[this.k + 1] = 1; // bkplus1 = b^(k+1)this.modulo = BarrettMu_modulo;this.multiplyMod = BarrettMu_multiplyMod;this.powMod = BarrettMu_powMod;
}
function charToHex(c)
{var ZERO = 48;var NINE = ZERO + 9;var littleA = 97;var littleZ = littleA + 25;var bigA = 65;var bigZ = 65 + 25;var result;if (c >= ZERO && c <= NINE) {result = c - ZERO;} else if (c >= bigA && c <= bigZ) {result = 10 + c - bigA;} else if (c >= littleA && c <= littleZ) {result = 10 + c - littleA;} else {result = 0;}return result;
}
function hexToDigit(s)
{var result = 0;var sl = Math.min(s.length, 4);for (var i = 0; i < sl; ++i) {result <<= 4;result |= charToHex(s.charCodeAt(i))}return result;
}
function biHighIndex(x)
{var result = x.digits.length - 1;while (result > 0 && x.digits[result] == 0) --result;return result;
}
function biFromHex(s)
{var result = new BigInt();var sl = s.length;for (var i = sl, j = 0; i > 0; i -= 4, ++j) {result.digits[j] = hexToDigit(s.substr(Math.max(i - 4, 0), Math.min(i, 4)));}return result;
}function RSAKeyPair(encryptionExponent, decryptionExponent, modulus, keylen){this.e = biFromHex(encryptionExponent);
this.d = biFromHex(decryptionExponent);
this.m = biFromHex(modulus);if (typeof(keylen) != 'number') { this.chunkSize = 2 * biHighIndex(this.m); }
else { this.chunkSize = keylen / 8; }this.radix = 16;this.barrett = new BarrettMu(this.m);
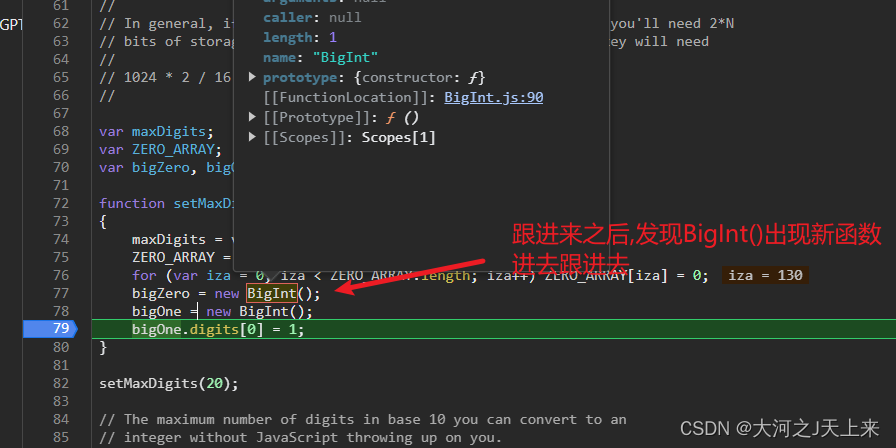
}function BigInt(flag)
{if (typeof flag == "boolean" && flag == true) {this.digits = null;}else {this.digits = ZERO_ARRAY.slice(0);}this.isNeg = false;
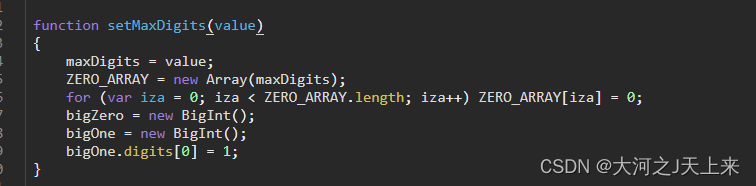
}function setMaxDigits(value)
{maxDigits = value;ZERO_ARRAY = new Array(maxDigits);for (var iza = 0; iza < ZERO_ARRAY.length; iza++) ZERO_ARRAY[iza] = 0;bigZero = new BigInt();bigOne = new BigInt();bigOne.digits[0] = 1;
}
var hexToChar = new Array('0', '1', '2', '3', '4', '5', '6', '7', '8', '9','a', 'b', 'c', 'd', 'e', 'f');
function reverseStr(s)
{var result = "";for (var i = s.length - 1; i > -1; --i) {result += s.charAt(i);}return result;
}
function digitToHex(n)
{var mask = 0xf;var result = "";for (i = 0; i < 4; ++i) {result += hexToChar[n & mask];n >>>= 4;}return reverseStr(result);
}
function biToHex(x)
{var result = "";var n = biHighIndex(x);for (var i = biHighIndex(x); i > -1; --i) {result += digitToHex(x.digits[i]);}return result;
}
function encryptedString(key, s, pad, encoding) {var a = new Array();                    // The usual Alice and Bob stuffvar sl = s.length;                      // Plaintext string lengthvar i, j, k;                            // The usual Fortran index stuffvar padtype;                            // Type of padding to dovar encodingtype;                       // Type of output encodingvar rpad;                               // Random padvar al;                                 // Array lengthvar result = "";                        // Cypthertext resultvar block;                              // Big integer block to encryptvar crypt;                              // Big integer resultvar text;                               // Text result/** Figure out the padding type.*/if (typeof (pad) == 'string') {if (pad == RSAAPP.NoPadding) {padtype = 1;} else if (pad == RSAAPP.PKCS1Padding) {padtype = 2;} else {padtype = 0;}} else {padtype = 0;}/** Determine encoding type.*/if (typeof (encoding) == 'string' && encoding == RSAAPP.RawEncoding) {encodingtype = 1;} else {encodingtype = 0;}if (padtype == 1) {if (sl > key.chunkSize) {sl = key.chunkSize;}} else if (padtype == 2) {if (sl > (key.chunkSize - 11)) {sl = key.chunkSize - 11;}}i = 0;if (padtype == 2) {j = sl - 1;} else {j = key.chunkSize - 1;}while (i < sl) {if (padtype) {a[j] = s.charCodeAt(i);} else {a[i] = s.charCodeAt(i);}i++;j--;}if (padtype == 1) {i = 0;}j = key.chunkSize - (sl % key.chunkSize);while (j > 0) {if (padtype == 2) {rpad = Math.floor(Math.random() * 256);while (!rpad) {rpad = Math.floor(Math.random() * 256);}a[i] = rpad;} else {a[i] = 0;}i++;j--;}if (padtype == 2) {a[sl] = 0;a[key.chunkSize - 2] = 2;a[key.chunkSize - 1] = 0;}/** Carve up the plaintext and encrypt each of the resultant blocks.*/al = a.length;for (i = 0; i < al; i += key.chunkSize) {/** Get a block.*/block = new BigInt();j = 0;for (k = i; k < (i + key.chunkSize); ++j) {block.digits[j] = a[k++];block.digits[j] += a[k++] << 8;}/** Encrypt it, convert it to text, and append it to the result.*/crypt = key.barrett.powMod(block, key.e);if (encodingtype == 1) {text = biToBytes(crypt);} else {text = (key.radix == 16) ? biToHex(crypt) : biToString(crypt, key.radix);}result += text;}/** Return the result, removing the last space.*/
//result = (result.substring(0, result.length - 1));return result;
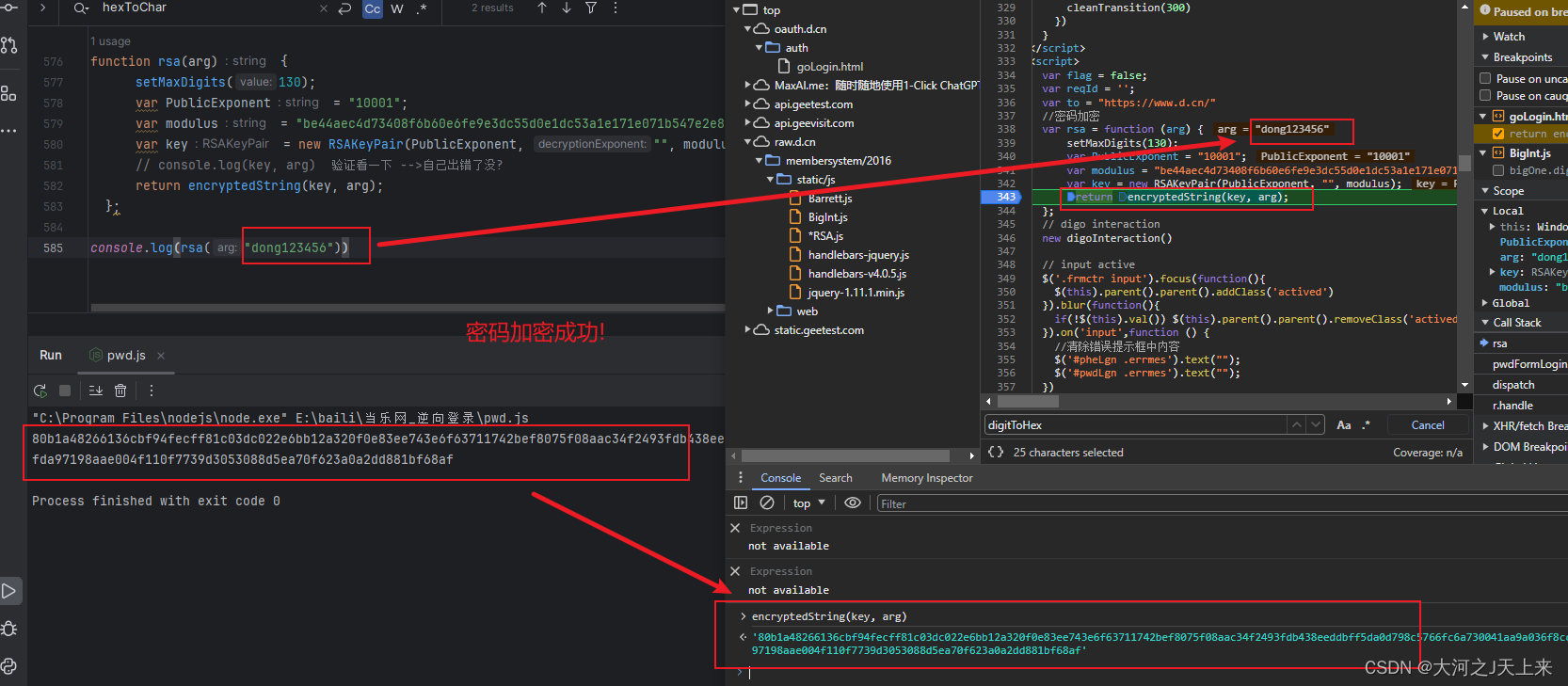
}function rsa(arg) {setMaxDigits(130);var PublicExponent = "10001";var modulus = "be44aec4d73408f6b60e6fe9e3dc55d0e1dc53a1e171e071b547e2e8e0b7da01c56e8c9bcf0521568eb111adccef4e40124b76e33e7ad75607c227af8f8e0b759c30ef283be8ab17a84b19a051df5f94c07e6e7be5f77866376322aac944f45f3ab532bb6efc70c1efa524d821d16cafb580c5a901f0defddea3692a4e68e6cd";var key = new RSAKeyPair(PublicExponent, "", modulus);// console.log(key, arg)  验证看一下 -->自己出错了没?return encryptedString(key, arg);};console.log(rsa("输入你的密码"))

---

(预告---下篇,详解本章的代码)

这篇关于JavaScript ＜关于逆向RSA非对称加密算法的案例(附原代码)＞--案例(五)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---