PAT甲级1130 Infix Expression：[C++题解]中缀表达式、二叉树中序遍历、dfs

本文主要是介绍PAT甲级1130 Infix Expression：[C++题解]中缀表达式、二叉树中序遍历、dfs，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

- 题目分析
- 题目链接

题目分析

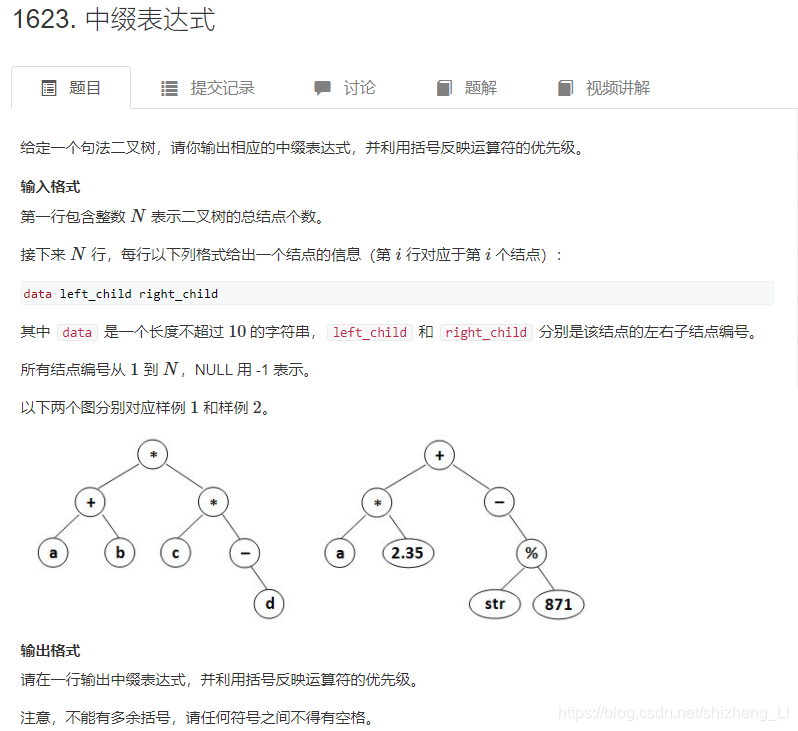
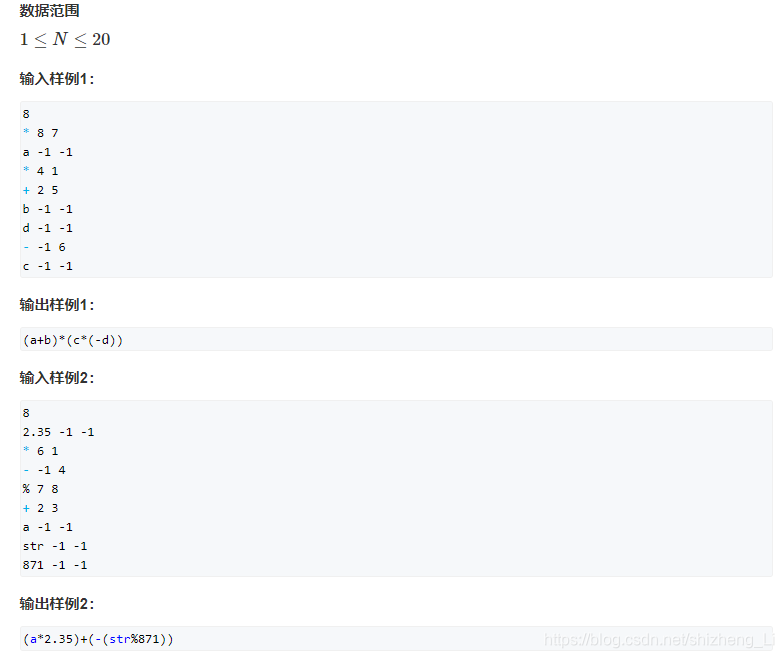
在这里插入图片描述

来源：acwing

分析：本题是借助中缀表达式这个背景，考察二叉树的中序遍历。本题需要注意的地方是加括号。左子树和右子树无脑加括号，只要不是叶结点。
所以写dfs的时候需要特判叶结点，叶结点不加括号。

这里直接用两个左右儿子数组存树l[N],r[N]。只要找到根结点，直接从根开始遍历即可。

ac代码

#include<bits/stdc++.h>
using namespace std;
const int N =30;int l[N],r[N]; 
string w[N]; //结点的值bool st[N]; //求根结点，st[i]有父节点记为true
bool is_leaf[N]; //is_leaf[i]  =true表示 i是叶结点//二叉树的深度优先遍历
//返回表达式的值
string dfs(int u){string left ,right; //左儿子，右儿子//左儿子存在if(l[u] != -1){left = dfs(l[u]);if(!is_leaf[l[u]]) left = "(" + left + ")";}//右儿子存在if(r[u] != -1){right = dfs(r[u]);if(!is_leaf[r[u]]) right = "(" +right +")";}//结点u左儿子不存在，右儿子不存在时才会到这一步//所以u是叶结点，return left + w[u] +right;}int main(){int n;cin >> n;for(int i =1; i<= n; i++){cin >> w[i] >> l[i] >> r[i];if(l[i] != -1) st[l[i]] =true;if(r[i] != -1) st[r[i]] = true;if(l[i] == -1 && r[i] == -1) is_leaf[i] =true;}int root =0;//没有父节点的结点是根结点for(int i=1; i<=n; i++)if(!st[i])  root = i;cout<<dfs(root)<<endl;}