【LeetCode:2646. 最小化旅行的价格总和

本文主要是介绍【LeetCode:2646. 最小化旅行的价格总和 | DFS + DP】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

🚀 算法题 🚀

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
🌲 作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚀 算法题 🚀

在这里插入图片描述

🍔 目录

- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- - ⚡ DFS + DP
  - - 🥦 求解思路
    - 🥦 实现代码
    - 🥦 运行结果
- 💬 共勉

🚩 题目链接

2646. 最小化旅行的价格总和

⛲ 题目描述

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的价格总和是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些非相邻节点并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：
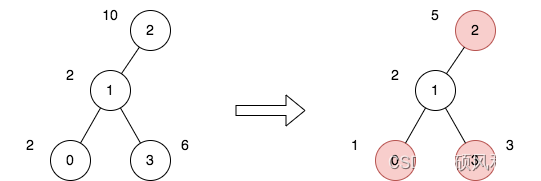
在这里插入图片描述

输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

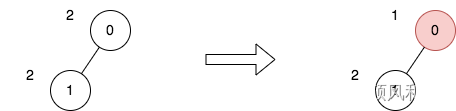
在这里插入图片描述

输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

1 <= n <= 50
edges.length == n - 1
0 <= ai, bi <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= starti, endi <= n - 1

🌟 求解思路&实现代码&运行结果

⚡ DFS + DP

🥦 求解思路

参考官方题解：最小化旅行的价格总和：方法一：深度优先搜索 + 动态规划
参考题解：暴力 DFS / 树上差分（Python/Java/C++/Go/JS/Rust）
实现代码如下所示：

🥦 实现代码

class Solution {private ArrayList<Integer>[] list;private int[] price,cnt;private int end;public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {this.list=new ArrayList[n];this.price=price;Arrays.setAll(list,e->new ArrayList<Integer>());for(int[] e:edges){list[e[0]].add(e[1]);list[e[1]].add(e[0]);}this.cnt=new int[n];for(int[] trip:trips){this.end=trip[1];dfs(trip[0],-1);}int[] res=dfs1(0,-1);return Math.min(res[0],res[1]);}public boolean dfs(int x,int father){if(x==end){cnt[x]++;return true;}for(int next:list[x]){if(next!=father&&dfs(next,x)){cnt[x]++;return true;}}return false;}public int[] dfs1(int x,int father){int noHalf=price[x]*cnt[x];int half=noHalf/2;for(int next:list[x]){if(next!=father){int[] res=dfs1(next,x);noHalf+=Math.min(res[0],res[1]);half+=res[0];}}return new int[]{noHalf,half};}
}