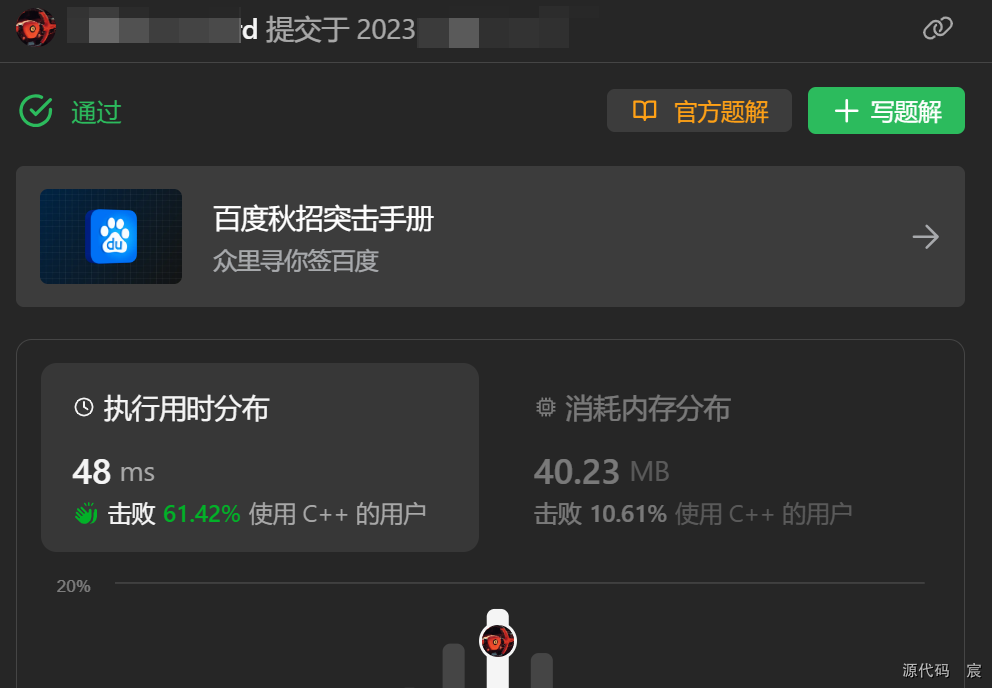
2646专题
【深度优先搜索】【图论】【树】2646. 最小化旅行的价格总和
作者推荐 【数位dp】【动态规划】【状态压缩】【推荐】1012. 至少有 1 位重复的数字 涉及知识点 深度优先搜索 图论 树 LeetCode2646. 最小化旅行的价格总和 现有一棵无向、无根的树,树中有 n 个节点,按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 a
SSL-ZYC 2646 线段树练习题三
题目大意: 给定一条长度为m的线段,有n个操作,每个操作有3个数字x,y,z表示把区间[x,y]染成颜色z。规定:线段的颜色可以相同。连续的相同颜色被视作一段。问x轴被分成多少段。 思路: 线段树 这道题与 线段树练习二 极其相似,唯一的区别在于count函数需要判断两根相交的线是否为同一个颜色。 代码: #include <cstdio>using namespace st
Leetcode—2646.最小化旅行的价格总和【困难】
2023每日刷题(五十三) Leetcode—2646.最小化旅行的价格总和 算法思想 看灵神的 实现代码 class Solution {public:int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {vector<i
Leetcode—2646.最小化旅行的价格总和【困难】
2023每日刷题(五十三) Leetcode—2646.最小化旅行的价格总和 算法思想 看灵神的 实现代码 class Solution {public:int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {vector<i
【LeetCode:2646. 最小化旅行的价格总和 | DFS + DP】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
Leetcode 2646. 最小化旅行的价格总和(暴力 DFS + 树形 DP)
Leetcode 2646. 最小化旅行的价格总和(暴力 DFS + 树形 DP)题目 现有一棵无向、无根的树,树中有 n 个节点,按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。每个节点都关联一个价格。给你一个整数数组 price ,其中 pric
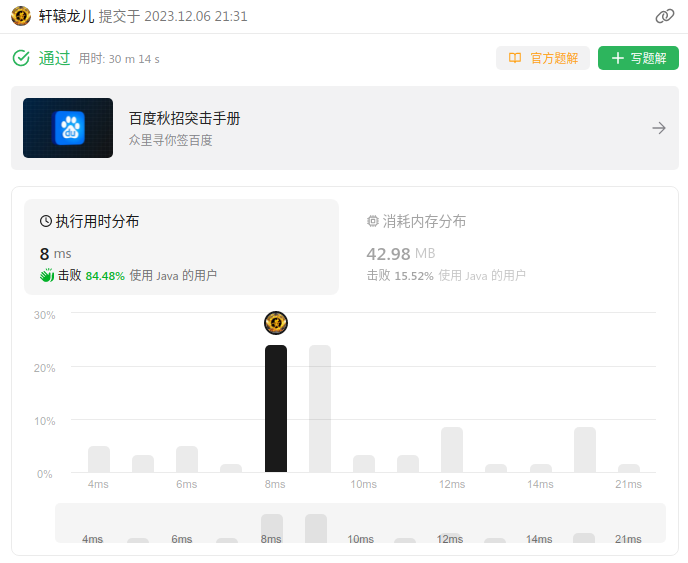
力扣每日一题:2646. 最小化旅行的价格总和(2023-12-06)
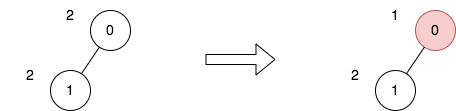
力扣每日一题 题目:2646. 最小化旅行的价格总和 日期:2023-12-06 用时:30 m 14 s 时间:8ms 内存:42.98MB 思路:先统计旅行中每个节点路过的次数(dfs方法),再计算减半后的价格之和的最小值(dp方法),最后比较下减半和未减半的价格。dp方法中,对于相邻的父子节点有两种情况: 如果父节点价格不变,那么子节点的价格取减半和不变两种情况的最小值如果父节点价格减半
LeetCode:2646. 最小化旅行的价格总和(dfs + 树形dp C++、Java)
目录 2646. 最小化旅行的价格总和 题目描述: 实现代码与解析: DFS + DP 原理思路: 2646. 最小化旅行的价格总和 题目描述: 现有一棵无向、无根的树,树中有 n 个节点,按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点
【每日一题】2646. 最小化旅行的价格总和-2023.12.5
题目: 2646. 最小化旅行的价格总和 现有一棵无向、无根的树,树中有 n 个节点,按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。 每个节点都关联一个价格。给你一个整数数组 price ,其中 price[i] 是第 i 个节点的价格。