【每日一题】2646. 最小化旅行的价格总和-2023.12.5

本文主要是介绍【每日一题】2646. 最小化旅行的价格总和-2023.12.5，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：

2646. 最小化旅行的价格总和

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

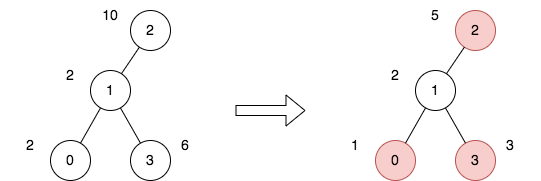
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

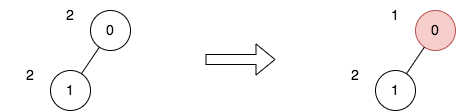
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

1 <= n <= 50
edges.length == n - 1
0 <= ai, bi <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= starti, endi <= n - 1

解答：

代码：

class Solution {public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {List<Integer>[] next=new List[n];for(int i=0;i<n;i++){next[i]=new ArrayList<Integer>();}for(int[] edge:edges){next[edge[0]].add(edge[1]);next[edge[1]].add(edge[0]);}int[] count=new int[n];for(int[] trip:trips){dfs(trip[0],-1,trip[1],next,count);}int[] pair=dp(0,-1,price,next,count);return Math.min(pair[0],pair[1]);}public boolean dfs(int node,int parent,int end,List<Integer>[] next,int[] count){if(node==end){count[node]++;return true;}for(int child:next[node]){if(child==parent){continue;}if(dfs(child,node,end,next,count)){count[node]++;return true;}}return false;}public int[] dp(int node,int parent,int[] price,List<Integer>[] next,int[] count){int[] res={price[node]*count[node],price[node]*count[node]/2};for(int child:next[node]){if(child==parent){continue;}int[] pair=dp(child,node,price,next,count);res[0]+=Math.min(pair[0],pair[1]);//node没有减半，因此可以取子树的两种情况的最小值res[1]+=pair[0];//node减半，只能取子树没有减半的情况}return res;}
}