课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文

本文主要是介绍课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、 论文内容

1.1 摘要

为准确测量旋转钻井时的钻具姿态，提出了一种新的信号处理方法。测斜仪旋转时，垂直于其旋转轴方向加速度计的输出信号中重力加速度信号分量具有周期性特征，以及非周期性离心加速度分量频率低于重力加速度信号分量频率的特征，用高通或带通滤波将非周期性离心加速度分量分离；对于常规滤波方法无法滤除的通频带内振动信号，增加一个对置加速度计，采取不同隔振措施补偿振动信号，滤除通频带内的振动信号。仿真分析表明，测斜仪旋转时离心力作用所导致的测斜仪加速度信息失真可以被高通或带通滤波器有效滤除；与旋转频率耦合的一个振动信号可以分解为2个频率的振动信号；采取不同隔振措施的对置加速度计，可以对振动信号进行补偿，滤除通频带内的振动信号。台架试验也证实，增加一个对置加速度计，并采取隔振措施棳可以补偿振动信号，滤除通频带内的振动信号。该处理方法为准确计算井斜角和工具面角等钻具姿态参数提供了技术手段。

1.2 加速度计的动态输出信号

   原论文中的测斜仪测斜原理部分就不再赘述，直接从下文开始。
  当加速度计静置时，输出信号基本为重力加速度信号；而当存在振动或因旋转产生离心力时，加速度计的输出信号中便混合了振动或离心加速度信号，即：$$s_f=s_g+s_v+s_e$$
  上式中，$s_g$为重力加速度信号，$s_v$为振动加速度信号，$s_e$为离心加速度信号。

1.3 重力加速度分量的提取方法

1.3.1 去除离心加速度

  井斜角传感器的三轴加速度计输出信号为：
$$s_x=s_{gx}+s_{vx}+s_{ex}$$ $$s_y=s_{gy}+s_{vy}+s_{ey}$$ $$s_z=s_{gz}+s_{vz}+s_{ez}$$
   $s_x,s_y,s_z分别是$$x,y,z$加速度计的输出信号。
  当井斜角传感器随钻柱旋转时，如图所示，如果z轴平行于钻柱旋转
轴线，则在轴方向不存在离心力,即$e_z=0$。此时，z轴方向重力分量不随转动改变，如果井斜角固定，其为常值，而z轴方向振动加速度可通过低通滤波滤除，于是有${\bar{s}}_z=s_{gz}$其中${\bar{s}}_z$为z轴加速度计低通滤波后输出信号。因为重力加速度已知，此时以静态测量时g的统计值为准，可以用下式计算井斜角：$cos\alpha =\frac{{\bar{s}}_z}{g}$
  设$g_{xy}$为重力加速度在xy平面内分量，则有:$$g_x=-g_{xy}cos\theta$$ $$g_y=-g_{xy}sin\theta$$
  旋转钻进时，工具面角因旋转而发生周期变化，因此由上式可知，x,y轴重力加速度分量也随之周期变化，其角频率与旋转角速度有关。因此，该情况下仅采用低通滤波并不能得到真实的重力加速度分量。
  钻柱匀速旋转时，离心加速度为常值，x、y轴重力加速度分量为周期信号，因此可用一个高通滤波器滤去直流成分，将离心加速度分量去除。于是有 :
$$s_x^{\prime }=s_{v_x}-s_{g_{xy}}cos\theta$$ $$s_y^{\prime }=s_{v_y}-s_{g_{xy}}sin\theta$$

1.3.2 去除振动加速度

  不同于钻柱静止或非旋转状态，钻柱旋转时，x、y轴上的振动信号分量耦合了旋转角度的变化。设$v_{xy}$为振动加速度在xy平面内分量,$v_{xy}$相对于高边的夹角为$\varphi$，${\omega }_v$为振动角频率，则有：$$v_x=v_{xy}sin(w_{v}t+\beta )cos(\theta -\varphi )$$ $$v_y=v_{xy}sin(w_{v}t+\beta )sin(\theta -\varphi )$$
  上式表明，一个周期振动信号在x、y轴上分量的幅值随钻柱旋转角度呈周期变化。设旋转角速度为${\omega }_r$，则有$\theta ={\omega }_{r}t+{\theta }_0$其中${\theta }_0$为t=0时刻的工具面角，可做如下变形 ：

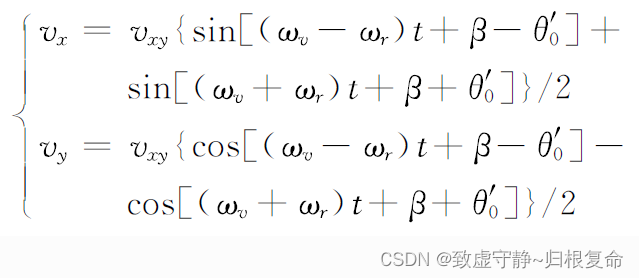
  上式表明，在钻柱旋转时，一个周期振动信号在x、y轴上的分量，耦合了旋转角频率，可分别用2个不同频率、不同相位的半幅值周期振动信号等效 。
  如果振动频率远大于钻柱旋转角速度(${\omega }_v\ge 3{\omega }_r$)，则振动信号所等效分解的2个分量的频率均远离重力加速度分量的变化频率，因此可以采,用合适的滤波器滤除振动信号。
  当${\omega }_v\approx 2{\omega }_r$，即振动信号的角频率接近钻柱旋转角频率的2倍时，振动信号中的低频率分量的角频率将接近旋转角速度，会对重力加
速度分量造成严重干扰，而且采用常规滤波方法很难滤除这种干扰。
  当${\omega }_v\approx {\omega }_r$时，振动信号低频分量接近于0，高频分,接近于$2{\omega }_r$，此时振动信号可以被有效滤除。
  由于旋转角速度较低，也就是说x、y轴方向重力加速度分量的变化频率较低(一般不超过4Hz)，则$2{\omega }_r+B$以下的振动信号，由于低频分量角频率(${\omega }_v-{\omega }_r$)与旋转角速度的绝对差值较小，一般难于完全滤除，而且振动信号的频率分量越接近旋转角速度，越难以滤除。此时用滤波后信号计算工具面角或井斜角会有较大误差。
  解决该问题的有效方法是椇增加1个加速度传感器与x或y轴背对放置，并对其采取隔振措施，使其对振动的敏感强度与对称轴有明显不同。例如与轴背对放置第4个加速度计-x，则其输出信号$s_{-x}=s_{-gx}-k{s}_{vx}+s_{ex}$，其中k为系数，于是有$$s_{vx}=(s_x+s_{-x}-2s_{ex})/(1-k)$$
  高通滤波器可将$s_{ex}$滤除，因此可写成$$s_{vx}=(s_x^{\prime }+s_{-x}^{\prime })/(1-k)$$
  现在问题的关键是确定系数k。测斜仪不旋转时，$s_{gx}$为常数，$s_{ex}$为0,因此k可由下式求得$$k=-s_x^{\prime }/s_{-x}^{\prime }$$
  注意，本论文没有讨论电路以及采样中的白噪声，因为白噪声可以通过低通或者电筒滤波器。所以一般在进行数据处理前，均需要进行低通或者带通滤波器处理。
  此外棳在进行振动信号补偿分析时，假定2个传感器的离心加速度大小相同，方向相反。事实上，由于装配等其他原因，2个传感器的离心加速度不一
定大小相同，方向相反。由于通常情况下，旋转钻进时，钻柱近似匀速旋转，离心加速度近似恒定，可利用高通或带通滤波器滤除，上文给出的方法仍然有效。

1.3 仿真及实验验证

二、往期回顾

课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法（基于磁场的测量系统）
课题学习(三)----倾角和方位角的动态测量方法（基于陀螺仪的测量系统）
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602

这篇关于课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---