本文主要是介绍一位半加法器,一位全加器,四位全加器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们这里的加法器只考虑一位的情况。
当我们两个一位相加的话,那么就有两个输入,两个输出,两个输入很好理解,就是两个个位上的数字,0或者是1,那么为什么需要有有个输出呢?难道不是输出一个数就好了吗?因为如果两个数字都是1的话,那么就要考虑到进位的情况,所以这个时候就有了两个输出,一个是S,一个是C_out,其中的C_out就是表示输出的进位。那么这样的话就构成了一位的半加器。如下图:

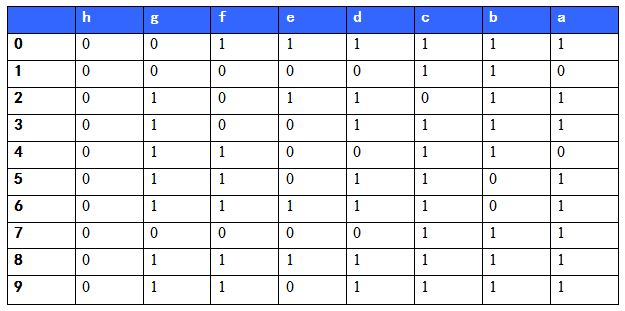
这个就是一位的半加法器。那怎么写出这种情况来的呢?其实就是将所有的A,B的输入情况全部枚举出来,然后写出对应的所有的S和C的情况,根据A,B和S的关系,然后推断出其中要使用那种逻辑电路才能写出来,总之大部分的关系都是可以通过一个逻辑符号表示出来的,如果一个不可以的话,那就写两个,或者是更多。
那为什么要引入全加法器呢?半加法器实现不了吗?原来半加法器只能实现个位的加减法,而十位,百位这些在中间的为主,如果低位有进位的话,那么就还需要一个出入的变量进行想加,所以得加入低位的进位C_in进行想加。那么这个时候有了三个输入的想加的变量,而一个半加法器只能同时进行两个数字的计算,这样的话就需要两个半加器进行计算就好了。我们可以将两个半加器的想加当做是两个阶段进行计算,第一个半加器的相加是旧相加,第二个半加器的相加是新相加,故而第一个半加器输出的C是C_旧,第二个半加器输出的是C_新。我们假设有一个十位上的A,B两个数字相加,然后有一个个位上的进位,C_in,那么首先,A,B先进行一个半加器的想加,输出的是一个十位上的数字,同时还有一个向高位的进位,C_旧,那么由于个位上的进位需要到十位上进行一个计算,所以第一次半加器计算的记过S需要和C-in进行第二次计算,计算出十位上的S和百位上的进位C-新,此时第二次算出来的S才是真正要计算出去的S,因为已经经过了所有十位上的计算,而百位上的进位,有两个,一个是C-旧,一个是C-新,这个时候要根据两个的值最后求出一个最后输出的C-out。实际上我们知道,如果一开始A,B进位的话,那么输入到第二个加法器中的S一定是0,因为最大就是两个1相加,故而第二个加法器中的C-新最大为1,即两个C不可能同时为1,即不能同时进位,故而C-旧和C新就只有三种情况(1,0)(0,1)(0,0)就只有这三种情况,而最后输出的C_out结果分别是他们两个数相加,为了避免再使用一次加法器,这个时候就需要用一个逻辑门来实现这个功能,显然使用逻辑或门是最好的,完全可以包括所有的情况,所以有了以下的电路。

那么有了一位的全加器,可不可以实现四位,八位甚至是更高位数上的想加呢?答案是可以的,但是这里只演示四位的全加器。
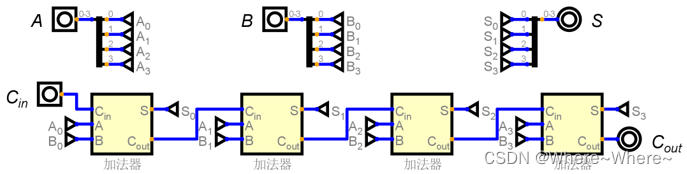
____________________________________________________________________________
其实减法也是同理,只不过是由进位变成了借位而已,也需要两个半减法电路去实现的,最终也是使用或门来连接的输出值,基本上和加法电路是一样的,不过需要注意的是,一次借位是2。
这篇关于一位半加法器,一位全加器,四位全加器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!