pku2480（欧拉函数的应用，推公式，积性函数）

本文主要是介绍pku2480（欧拉函数的应用，推公式，积性函数），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://162.105.81.212/JudgeOnline/problem?id=2480

题意：给定N(int)  求 ∑gcd(i,N) 1<=i<=N。

分析：一看这题的数据就知道不能暴力的，要用到欧拉函数分解才行的，只是自己的数论还不成熟，想了好久都没有解法；

最后看了牛人的解题报告才弄明白的；

此题解法：对于gcd(M,N)=i 有Ci个M满足此式 答案便是∑(Ci*i)gcd(M,N)=i  <=> gcd(M/i,N/i)=1 而求gcd(M/i,N/i)=1 有多少个M/i满足 这便是欧拉函数Phi()的定义所以就转化为了求Phi(N/i)枚举每个 M|N  求出Phi(N/i)  答案便是 ∑(Phi(N/i)*i)那么如何枚举每个  M|N 呢？

很简单 枚举1到sqrt(N)的所有整数，所有的约数便是 i|N 和 (N/i)|N。

#include<iostream> #include<cmath> using namespace std; bool s[50005]; int prime[50005]; void Prime()//求素数 { int i,j; for(i=2; i<50005; i++) if(!s[i]) { for(j=i<<1; j<50005; j+=i) s[j] = 1; } for(i=2; i<50005; i++) if(!s[i]) prime[++prime[0]] = i; } int euler(int x) //求欧拉函数值， { int i, res = x; for(i=1; i<=prime[0] && prime[i]<(int)sqrt(x*1.0)+1; i++) if(x % prime[i] == 0) { res = res / prime[i] * (prime[i] - 1); while(x % prime[i] == 0) x /= prime[i]; } if(x > 1) res = res / x * (x - 1); return res; } int main() { int n, i, j; __int64 ans; Prime(); while(scanf("%d", &n) != EOF) { ans = 0; for(i=1; i<=(int)sqrt(n*1.0); i++) //优化； { if(n % i == 0) { ans += (n/i) * (__int64)euler(i); if(n != i * i) ans += i * (__int64)euler(n/i); } } printf("%I64d/n",ans); } return 0; } 

还有别的解法是积性函数，因子分解；

 

（1）因为有性质

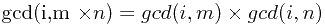  当时

所以gcd是积性函数

因为积性函数的和函数也是积性函数(《初等数论及其应用》P182),所以所求函数

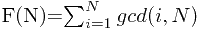是积性函数

问题简化到素数阶段,须求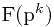,此时用到欧拉公式.因为有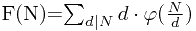

(易见因为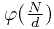代表的是从1到N中和N最大公约数gcd为d的数的个数)

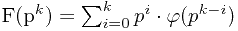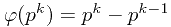所以,又因为则可求出。

（2）

 

容易证明gcd(i,n)是积性函数，即： 如果n = m1*m2 且gcd(i,m1*m2) = gcd(i,m1)*gcd(i,m2). 然后根据具体数学上的结论： 积性函数的和也是积性的，所以如果我们设所求答案是f(n) 则： f(n) = f(m1)*(m2) 其中，m1*m2 = n 且m1,m2互质！经过因子分解，那种只要求到f(p^k)就可以利用积性把所有结果相乘得到最后答案。

还要一个结论： f(n) = sum(p * phi(n/p))  其中p是n的因子，phi(n/p) 是从1到n有多少个数和n的gcd是p,  这个结论比较好证明的。

        所以求f(p^k)转化成求phi(p^i) i =0....k;  而根据公式phi(p^i) = (p-1)*p^(i-1)可以求出，这样整个问题就解决了。  具体算法过程要先把1到50000的素数求出来便于分解因子。

 

 

这篇关于pku2480（欧拉函数的应用，推公式，积性函数）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---