LeetCode 1038. 从二叉搜索树到更大和树：（反）中序遍历

本文主要是介绍LeetCode 1038. 从二叉搜索树到更大和树：（反）中序遍历，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【LetMeFly】1038.从二叉搜索树到更大和树：（反）中序遍历

力扣题目链接：https://leetcode.cn/problems/binary-search-tree-to-greater-sum-tree/

给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下， 二叉搜索树 满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

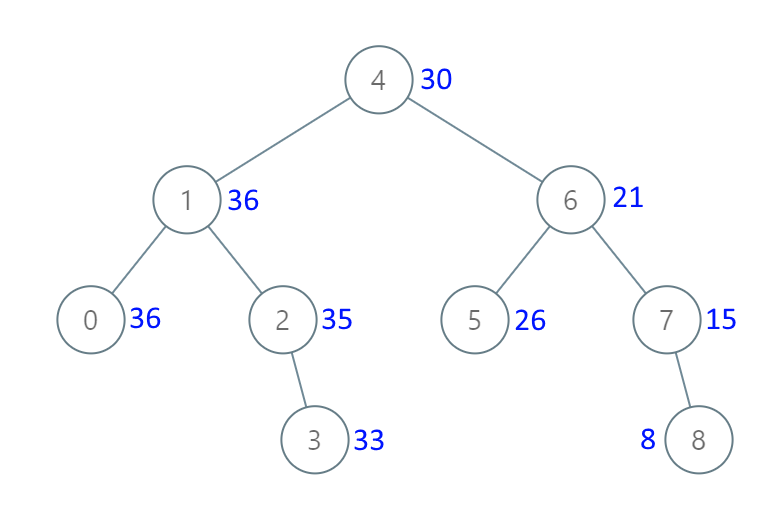
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

提示：

树中的节点数在 [1, 100] 范围内。
0 <= Node.val <= 100
树中的所有值均 不重复 。

注意：该题目与 538: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ 相同

方法一：（反）中序遍历

二叉搜索树的中序遍历（左子→根→右子）得到的序列是非递减序列。反之，右子→根→左子得到的序列就是非递增序列。

“反中序遍历”的过程中，我们只需要使用一个遍历记录“当前所有遍历过的元素的和”，即为大于等于当前元素的所有元素的和。

时间复杂度 $O (n)$ ，其中 $n$ 是二叉树节点个数
空间复杂度 $O (n)$ ，最坏情况下二叉树退化成一条链，递归占用空间 $O (n)$

AC代码

C++

class Solution {
private:int last;void dfs(TreeNode* root) {if (!root) {return;}dfs(root->right);last += root->val;root->val = last;dfs(root->left);}
public:TreeNode* bstToGst(TreeNode* root) {last = 0;dfs(root);return root;}
};

Python

# from typing import Optional# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = rightclass Solution:def dfs(self, root: Optional[TreeNode]) -> None:if not root:returnself.dfs(root.right)self.last += root.valroot.val = self.lastself.dfs(root.left)def bstToGst(self, root: TreeNode) -> TreeNode:self.last = 0self.dfs(root)return root