机器学习|FP-Growth

在上篇文章频繁项集挖掘实战和关联规则产生.中我们实现了Apriori的购物篮实战和由频繁项集产生关联规则, 本文沿《数据挖掘概念与技术》的主线继续学习FP-growth。因《数据挖掘概念与技术》中FP-growth内容过于琐碎且不易理解，我们的内容主要参考了《机器学习实战》第12章的内容。本文是对书中内容的通俗理解和代码实现,更详细的理论知识请参考书中内容, 本文涉及的完整jupyter代码和《机器学习实战》全书配套代码包, 可以在我们的 “数据臭皮匠” 中输入"第六章3" 拿到

Apriori算法是经典算法, 但它也有比较明显的缺点，主要有两个：

1、它可能需要产生大量候选集， 如果有10^4个频繁1项集, Apriori需要产生多达10^7个候选2项集

2、 每一步从候选k项集, 到频繁k项集都需要完整的扫描数据集, 反复扫描完整数据集开销很大

有没有某种方法可以不产生大量候选项集且不需要反复扫描完整数据集就可以产生频繁项集呢, 有! 他就是FP-growth(Frequent-Parttern Growth) 频繁模式增长。

FP-growth先将数据集压缩到一颗FP树（频繁模式数），再遍历满足最小支持度的频繁一项集，逐个从FP数中找到其条件模式基，进而产生条件FP树，并产生频繁项集。

一、基础概念

1、FP树

FP 树将每个集合以路径的方式存储在树中, 从根节点开始, 每个条路径上的节点按其出现频数递减. 存在相似元素的集合会共享树的一部分, 只有当集合之间出现不同时, 树才会分叉. 图示如下(左图是数据, 右图是最小支持度为 3 的 FP树)

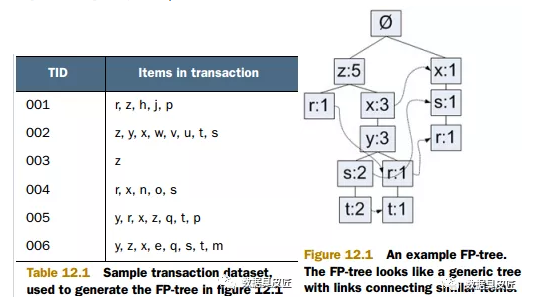
2、Header表

链表, 每个节点存放的是某一元素项, 及其在所有集合中出现的总次数, 以及指向FP树各个分支上同样元素的指针. 从Header表, 可以快速定位到各个分枝上的元素. 头指针表图示如下:

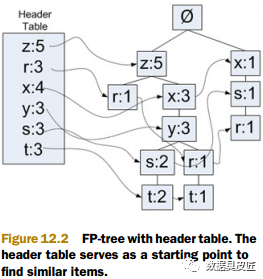
3、条件模式基

从header表中的单个频繁元素开始, 对每个路径中的此元素, 向根节点回溯, 每一条回溯路径上的节点都组成一个集合. 即前缀路径.

4、条件FP树

使用 3 中的得到的各个前缀路径, 作为新的数据集合, 并按 1 中的方法构造出来的 FP 树, 即为 条件FP树.在构造条件 FP 树时, 同样要通过最小支持度来淘汰非频繁项

二、算法描述

1. 构造FP树

1.1) 遍历完整数据集， 对每个元素计数，每个元素在数据集中出现的次数组成header表（仅包含大于最小支持度的项）

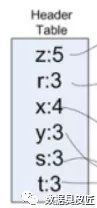
1.2）遍历每个集合, 对此集合中的元素, 按其在总数据集中出现的次数排序, 并去除掉未达到最小支持度的元素.

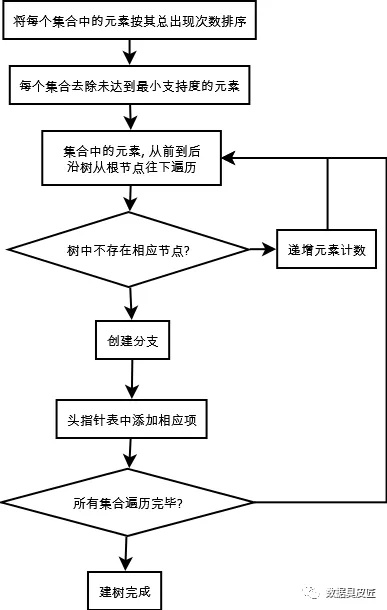
1.3）对每个集合, 从树的根节点依次往下插入, 如果节点已存在, 则递增节点的计数值, 否则创建一个分支，如下图:

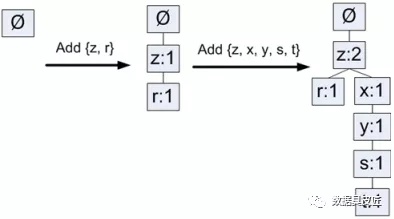
1.4）新加入节点的同时， 需要将新结点与header表建立连接， 如果header表的该元素已经有节点与之连接， 新结点就连接到该元素对应连接链的末端

1.5）循环 (3) -> (4), 直至所有集合操作完毕

# 树节点
class treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccur         # 计数值self.nodeLink = None          # 连接相似变量