第一类瑞利索末菲标量衍射模型的方孔衍射的空间像计算（附python计算代码）

本文主要是介绍第一类瑞利索末菲标量衍射模型的方孔衍射的空间像计算（附python计算代码），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

https://zhuanlan.zhihu.com/p/624292239
Goodman, J. W. (2004). Introduction to Fourier Optics.

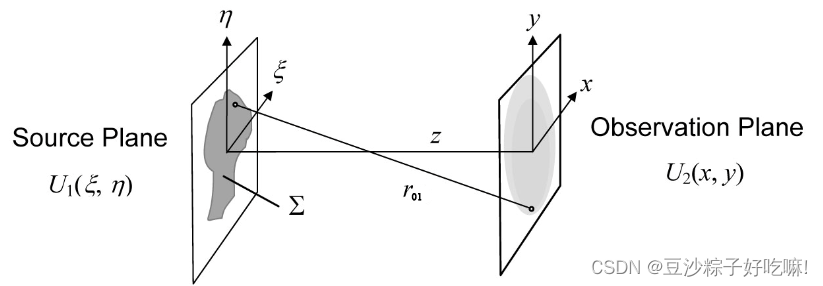
RS type 1 衍射空间像计算

$$U_1(P_0)=\frac{1}{j\lambda }\int {\int }_{\Sigma }U(P_1)\frac{exp(jk{r}_{01})}{r_{01}}\cos (\vec{n},\overrightarrow{r_{01}})ds$$

直接计算该积分，需要二重循环，然后再二重循环遍历观测屏上的点，效率低下

傅里叶变换

二重积分在$\Sigma$上进行计算。将ds写为dxdy的形式，z为观测平面与源平面的距离，有
$$\cos (\vec{n},\overrightarrow{r_{01}})=\frac{z}{r_{01}}$$
$$r_{01}=\sqrt{(x-x_0{)}^2+(y-y_0{)}^2+(z-z_0{)}^2}$$

$$\begin{array}{rl}{U}_1(P_0)& =\frac{1}{j\lambda }\int {\int }_{\Sigma }U(x,y)\frac{exp(jk{r}_{01})}{r_{01}}\cos (\vec{n},\overrightarrow{r_{01}})dxdy\\ & =\int {\int }_{\Sigma }U(x,y)V(x,y)dxdy\end{array}$$

V ( x , y ) = 1 j λ e x p ( j k ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 ) ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 z ( x − x 0 ) 2 + ( y − y 0

这篇关于第一类瑞利索末菲标量衍射模型的方孔衍射的空间像计算（附python计算代码）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---