本文主要是介绍Deep coral: Correlation alignment for deep domain adaptation. ECCV 2016. Domain Adaptation,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
** Sun, Baochen, and Kate Saenko. “Deep coral: Correlation alignment for deep domain adaptation.” ECCV. Springer, Cham, 2016. **
结构如图:
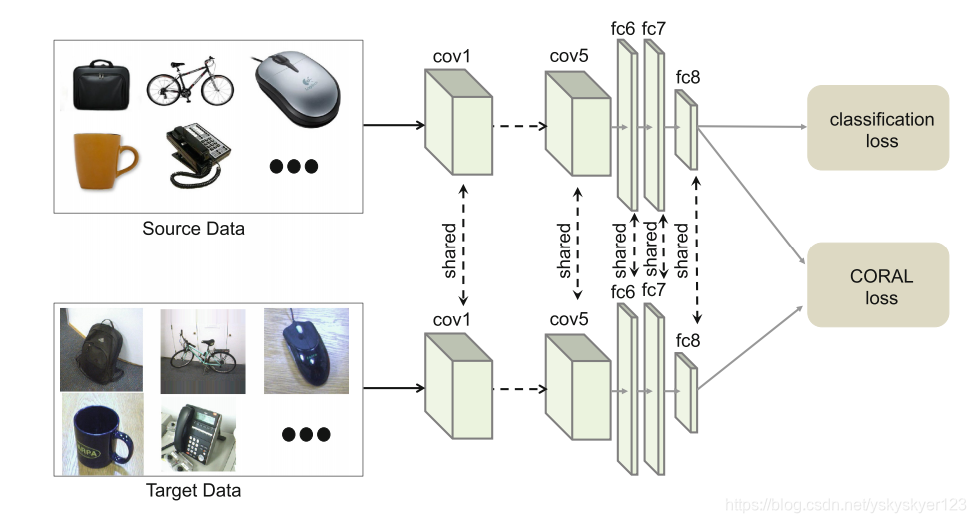
两个损失函数:
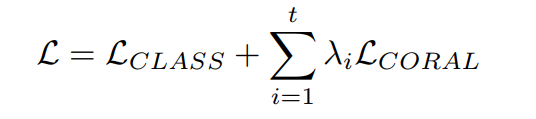
其中 L C L A S S \mathcal{L}_{CLASS} LCLASS为分类损失, L C O R A L \mathcal{L}_{CORAL} LCORAL:

C S C_S CS和 C T C_T CT为样本协方差 (二阶统计量),反映了feature map上各位置的相关性。 其中D_S矩阵的每一行代表代表一个feature map。 C S C_S CS和 C T C_T CT的行数= C S C_S CS和 C T C_T CT的列数=feature map维度。

CORAL Loss系数为0时,训练过程中CORAL distance测量值变化情况:
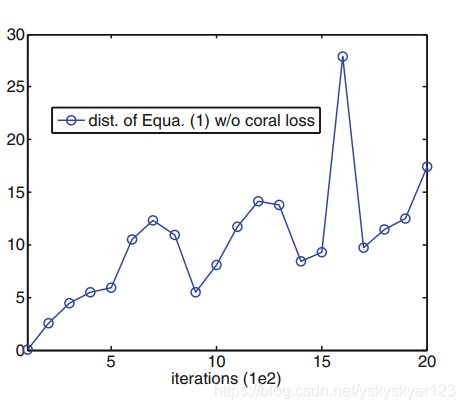
上图证明了CORAL Loss的有效性。


原文表明:没有CORAL Loss直接fine-tuning容易对source domain的数据过拟合。
这里复习下样本方差为无偏估计量:
S 2 = ∑ ( x i − x ˉ ) 2 n S^2= \frac{\sum (x_i - \bar{x} )^2 }{n} S2=n∑(xi−xˉ)2
证明:
E ( s 2 ) = 1 n − 1 E [ ∑ ( x i − x ˉ ) 2 ] = ∑ E ( x i 2 − 2 x ˉ x i + x ˉ 2 ) n − 1 = n E 2 ( x ) − 2 n E ( x ˉ 2 ) + n E ( x ˉ 2 ) n − 1 = n E 2 ( x ) − n E ( x ˉ 2 ) n − 1 = n E 2 ( x ) − n D ( x ˉ ) − n E 2 ( x ˉ ) n − 1 = n E 2 ( x ) − n D ( x ˉ ) − n E 2 ( x ) n − 1 = n E 2 ( x ) − n E 2 ( x ) − n D ( x ˉ ) n − 1 = n D ( x ) − n D ( x ) n n − 1 = D ( x ) \begin{aligned} E(s^2)&= \frac{1}{n-1} E[ \sum(x_i -\bar{x})^2 ] \\ &=\frac{\sum E(x_i^2-2\bar{x}x_i +\bar{x}^2 ) }{n-1} \\ &=\frac{nE^2(x)-2nE(\bar{x}^2)+nE(\bar{x}^2)}{n-1} \\ &=\frac{nE^2(x)-nE(\bar{x}^2)}{n-1} \\ &=\frac{nE^2(x)-nD(\bar{x})-nE^2(\bar{x}) }{n-1} \\ &=\frac{nE^2(x)-nD(\bar{x})-nE^2(x) }{n-1} \\ &=\frac{nE^2(x)-nE^2(x) -nD(\bar{x})}{n-1} \\ &= \frac{nD(x)-\frac{nD(x)}{n}}{n-1}\\ &=D(x) \end{aligned} E(s2)=n−11E[∑(xi−xˉ)2]=n−1∑E(xi2−2xˉxi+xˉ2)=n−1nE2(x)−2nE(xˉ2)+nE(xˉ2)=n−1nE2(x)−nE(xˉ2)=n−1nE2(x)−nD(xˉ)−nE2(xˉ)=n−1nE2(x)−nD(xˉ)−nE2(x)=n−1nE2(x)−nE2(x)−nD(xˉ)=n−1nD(x)−nnD(x)=D(x)
注意:
E ( x ) ≠ x ˉ ∑ ( − 2 E ( x i ) x ˉ ) ≠ − 2 n E ( x ) E ( x ) = E ( x ˉ ) D ( x ˉ ) = E ( x ˉ 2 ) − E 2 ( x ˉ ) \begin{aligned} E(x) &\neq \bar{x} \\ \sum (-2E(x_i) &\bar{x}) \neq -2nE(x) \\ E(x) &= E(\bar{x}) \\ D(\bar{x})&=E(\bar{x}^2)-E^2(\bar{x}) \end{aligned} E(x)∑(−2E(xi)E(x)D(xˉ)̸=xˉxˉ)̸=−2nE(x)=E(xˉ)=E(xˉ2)−E2(xˉ)
类似于 S 2 = ∑ ( x i − x ˉ ) 2 n S^2= \frac{\sum (x_i - \bar{x} )^2 }{n} S2=n∑(xi−xˉ)2
样本协方差 = ∑ ( x i − x ˉ ) ( y i − y ˉ ) n − 1 = ∑ x i y i − n x ˉ y ˉ n − 1 = \frac{\sum (x_i-\bar{x}) (y_i-\bar{y}) }{n-1}= \frac{ \sum x_iy_i -n \bar{x}\bar{y} }{n-1} =n−1∑(xi−xˉ)(yi−yˉ)=n−1∑xiyi−nxˉyˉ
这篇关于Deep coral: Correlation alignment for deep domain adaptation. ECCV 2016. Domain Adaptation的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!