GA在一般线性或非线性规划问题中的应用

综述

本文在进入正题前，加入了数学建模的方法作为说明铺垫，虽然简单但是是个很好示例。
首先说明，在求解线性与非线性问题时lingo软件是一个很好的选择。当然，如果能用遗传算法求解，在保证其算法和代码的正确性的前提下，选择该方法也是一个不二之选。读者会其他更好的优化软件，也可以权当了解拓展视野；对于笔者，也是一个拓展提高的机会。

问题叙述

背景

背景：结合市场行情和实践的背景情况，我们对可能的风险进行讨论。国家推出促进小资企业的创新创业政策，可以说政策风险很小，甚至说经济政策甚至是一个优势，所以我们不予考虑；之后在忽略去财务风险之后，我们综合考虑的风险有以下五种：行业风险、技术开发风险、经营管理风险、市场开拓风险、生产风险。

分析

分析：对于风险的控制，我们不能都做到减小，只能说是相对当前所面对的情形下的最低风险，即转化为一个规划问题的最优解。但是在进行求解风险时，应对着重处理影响力最大的风险，即是占比风险权重最大的一些部分。综上所述，我们先通过进行求解各风险在问题中的占比权重，然后通过风险最小和利益最大的线性或非线性规划问题，进行求解最好的投资方式，从而对风险进行控制。因为所给的风险种类小，用层次分析法进行求解简单而准确；之后再通过解规划模型得出实际情况下的最优风险控制方案。

优化目标

优化目标：在风险最小的情况下获得做大利润。我们都知道，风险越高获益越大，显然这是一个矛盾性的问题。接下来我们用数学语言对其进行描述：

模型建立

模型求解

  在不失一般性的前提下，我们假定我们的资本是1w元。五种风险分别命名为甲、乙、丙、丁、戊，在权重确定
后得到获利权重向量w=（3.8，1.5，2.6，0.7，1.4），其中X=（x1,x2,x3,x4,x5），总收益为w*X’。而损失的权重向量为l=（-2.9，-0.21，-1.52，-0.33，-2.0），总损失为l*X’。但是风险的产生是以概率存在的，
我们设这个概率向量p=（0.5，0.05，0.15，0.1，0.2）。

下面是对遗传算法解决问题的概述和流程图
初始种群：初始种群大小为20，这里的基因型采用以分量和为1的向量来表示，而不是采用二进制。迭代次数为100，变异概率0.1，交叉概率0.9，选择时采用轮盘赌进行选择。适应度函数即为模型中的目标函数。
交叉：从种群中随机选取2个样本作为父代，进行交叉。
选择：选择适应度大的个体得以保存下来。
变异：在概率较小的情况下，对基因型进行值的改变，稀释其他未变异基因比重，得到新的个体。
迭代：如此循环往复进行迭代100次，最终得出较优的解。

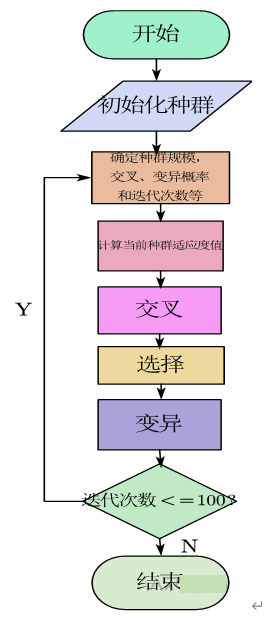
图1 流程示意图

代码

完整代码大家可以参考我的网址
https://download.csdn.net/download/wlfyok/12604709

% 下面是对于初始条件的设定
gen = 10000;
cp = 0.9;    % crossoverpossibility
mp = 0.1;    % mutatepossibility
popsize = 20;
pop = zeros(20,5);% 种群初始化
for i = 1:20pop(i,:) = rand(1,5);pop(i,:) = normalize(pop(i,:));
end% 保留每次最高值，以便后续画图
maxvalue = zeros(100,1);% GA算法
for k = 1:gen% 计算初始种群的适应度值for i = 1:20value(i) = fitness999(pop(i,:));end% 轮盘赌选择sizement = 4;for i = 1:sizementparent(i,:) = pop(randi(20),:); endfor i = 1:sizementresult(i) = fitness999(parent(i,:));endmost = 1;for i = 1:sizementif result(i) > result(most)most = i;endendfor m = 1:20if result(most) == value(m)local1 = m;endendparent1 = parent(most,:);for i = 1:sizementparent(i,:) = pop(randi(20),:); endfor i = 1:sizementresult(i) = fitness999(parent(i,:));endmost = 1;for i = 1:sizementif result(i) > result(most)most = i;endendfor n = 1:20if result(most) == value(n)local1 = n;endendparent2 = parent(most,:);[offspring1,offspring2] = crossover999(parent1,parent2);pop(local1,:) = offspring1;pop(local2,:) = offspring2;            % 交叉num = randperm(20,1);pop(num,:) = mutate999(pop(num,:));    % 变异% 计算当前种群的适应度，并记录for j = 1:20value(j) = fitness999(pop(j,:));endmaxvalue(k) = max(value);
end
plot(maxvalue)

完整代码大家可以参考我的网址
https://download.csdn.net/download/wlfyok/12604709

结论与分析

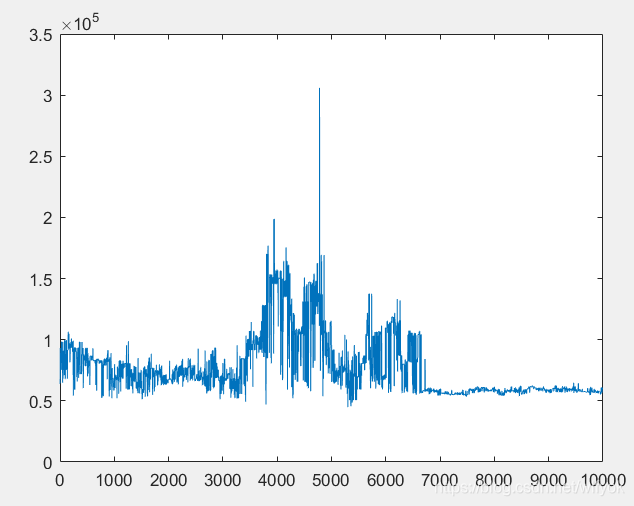
笔者一开始以为迭代100次就能得到结果，但不尽如人意，当笔者尝试到10000次时，发现结果收敛了，当然每次运行的结果可能不太一样，但大多类似于此图的情况，所以就把它当作结果图了。当然了，算法的设计上可能有一些问题，因为迭代的次数太多，而且出现不收敛的情况也不是太少，或许这个问题本来就没有一个收敛的值，当然我们不去讨论这种情况。
实验结果表面，最终的结果表明，我们的收益是0.6*10e5，说明这个项目是盈利的，在其他情况不变的情况下，带入此种情况的投资占比，即可得到我们的最大收益了。

一起进步呀

如果大家对觉得笔者写的文章有什么不清楚的地方，欢迎在评论区指出。
再者，如果大家有想要讨论相关的问题也可以在评论区留言或私信。
如果有需要智能算法求解的问题，也可以发给笔者，笔者可以试试，和大家一起讨论学习。
最后，如果大家觉得还行的话，点一个赞赞再走呗，笔芯！