协同滤波模型的推荐算法（ACM暑校-案例学习）

本文主要是介绍协同滤波模型的推荐算法（ACM暑校-案例学习），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

基于协同滤波的推荐技术可以细分为基于用户的协同过滤方法、基于产品的协同过滤方法、基于模型的协同过滤方法；本博文进行了一一测试。

1. 数据准备、评价指标

由于协同滤波模型需要用到用户的行为，这里选用MovieLen数据集进行测试研究。

MovieLen是明尼苏达大学计算机科学系GroupLens研究中心开发和维护的，也是最常用于测试协同滤波算法性能的公开数据集之一。Movielens提供了大量电影的用户评分。完整的版本包括超过了26000000的电影评分，他们来源于270000用户观看45000部电影的体会。GroupLens网站上提供的数据集不再提供用户人口统计信息。因此，这里使用Prajit-Datta在kaggle上提供的部分数据集。

数据下载

下载地址：https://www.kaggle.com/prajitdatta/movielens-100k-dataset/data

该数据集包括：1682部电影上943名用户的100000个评分（1-5）。每个用户至少为20部电影打分。该数据集也为用户提供简单的人口统计信息（年龄、性别、工作等）。这些数据是在1997年9月19日至1998年4月22日的七个月期间通过Movielens网站（movielens.umn.edu）收集的。此数据已被清除-从该数据集中删除了评分低于20或没有完整人口统计信息的用户。

数据浏览

在解压文件中，只需要使用u.date/ u.user/ u.item三个文件。

① 查看用户图谱文件

import pandas as pd# load the u.user file into a dataframe
u_cols = ['user_id', 'age', 'sex', 'occupation', 'zip_code']
users = pd.read_csv('C:/Users/Administrator/Desktop/RecoSys/data/movielens/u.user', sep='|',names=u_cols, encoding='latin-1')
users.head()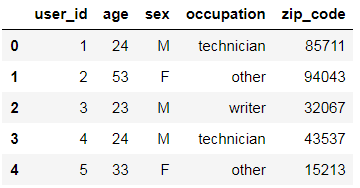

可以看到，u.user文件中主要包含的用户图谱，如年龄，性别，职业，zip_code。

② 查看电影描述文件

i_cols = ['movie_id', 'title', 'release date', 'video release date', 'IMDB URL', 'unknow', 'Action', 'Adventure', 'Animation', 'Children\'s', 'Comedy', 'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir', 'Horror', 'Musical', 'Mystery', 'Romance', 'Sci-Fi', 'Thriller', 'War','Western']
movies = pd.read_csv('C:/Users/Administrator/Desktop/RecoSys/data/movielens/u.item',sep='|', names=i_cols, encoding='latin-1')
movies.head()

可以看出，u.item文件中主要提供了电影的名字、发行时间、IMDB URL和题材等信息。因为，本编博客主要研究的是协同滤波算法，因此，电影中的题材等是用不到的，只需要保留movie_id和title就好。

movies = movies[['movie_id', 'title']]
movies.head()

③ 查看用户对电影评分文件

r_cols = ['user_id', 'movie_id', 'rating', 'timestamp']
ratings = pd.read_csv('C:/Users/Administrator/Desktop/RecoSys/data/movielens/u.data',sep='\t', names=r_cols, encoding='latin-1')
ratings.head()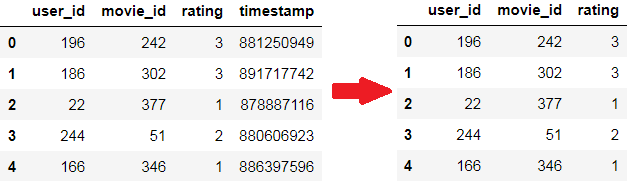

训练数据 training data & 测试数据 test data

DataFrame包含从1-5的用户对电影的评分。因此，可以将该问题建模为监督学习的实例，目的在于预测给定用户和电影的评分。虽然电影的分数只是1-5的五个离散值，其实质仍为回归问题。考虑用户对电影的真实评分是5：分类模型不能区分预测评分为1和4的情况。分类模型会将1-4的评分都视为错误分类。然而，回归模型却不是这样子，其对rating=4的惩罚远远大于rating=1的情况。

对于监督模型的学习，重要的一步在于训练集和测试集的划分。在本次试验中，用户评分数据中的75%用作模型训练，25%用于模型测试

from sklearn.model_selection import train_test_split
X = ratings.copy()
y = ratings['user_id']
# split into training and test datasets, stratified along user_id
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, stratify=y, random_state=42)>>> 
X_train.shape = (75000, 3)
X_test.shape = (25000, 3)

评估方法

这里选用根均方差（RMSE=root-mean-square-error）对模型的推荐性能进行评估。其Python实现如下所示：

from sklearn.metrics import mean_squared_error
from numpy as npdef rmse(y_true, y_pred):return np.sqrt( mean_squared_error(y_true, y_pred) )# Function to compute the RMSE score obtained on the testing set by a model
def score(cf_model):# Construct a list of user-movie tuples from the testing datasetid_pairs = zip(X_test['user_id'], X_test['movie_id'])# Predict the rating for every user-movie tupley_pred = np.array([cf_model(user, movie) for (user, movie) in id_pairs])# Extract the actual ratings given by the users in the test datay_true = np.array(X_test['rating'])# Return the final RMSE scorereturn rmse(y_true, y_pred)

2. 基于用户的协同过滤推荐算法实例 Users-based

基于用户的协同推荐算法把主要的研究精力放在用户角度，实质上就是具有相同兴趣的用户群体进行聚类，然后对相同类群的用户进行产品推荐。核心在于对高度稀疏的用户-产品矩阵进行预测和填充。PANDAS提供了一个非常好用的函数pivot_table去构造rating矩阵：

# Build the ratings matrix using pivot_table function
r_matrix = X_train.pivot_table(values='rating', index='user_id', columns='movie_id')
r_matrix.head(5)

该矩阵就是推荐领域最最重要的了：①用户-产品矩阵是高度稀疏的；②实际应用过程中，从用户和产品两个维度考虑，评分矩阵是非常非常巨大的。

均值Mean角度初步考虑

首先可以构建一个最简单的协同过滤算法，只需输入用户ID和电影ID，并输出所有看过的用户对该电影的平均评分。用户之间没有区别。换言之，每个用户的评分被赋予相等的权重。其中，有一种完全可能异常情况：有些电影只能在测试数据集进行访问，而在训练数据集不存在。该情况下，我们直接设置一个baseline，将其默认赋值为3.0。

# User Based Collaborative Filter using MEan Rating
def cf_user_mean(user_id, movie_id):# Check if movie_id exists in r_matrixif movie_id in r_matrix:# Compute the mean of all the ratings given to the moviemean_rating = r_matrix[movie_id].mean()else:# Default to a rating of 3.0 in the absence of any informationmean_rating = 3.0return mean_rating# Compute RMSE for the Mean model
score(cf_user_mean)>>> 1.0234701463131335

该方法仅仅适合讨论研究，是没有实际应用价值的：一方面，用户对产品的评分肯定会有偏好；另一方面，大部分少数群体的兴趣没有被认真关注。一种合适的改进方法是采用加权平均weighted mean。

加权均值weighted mean角度考虑

在前面的模型中，我们为每一个用户分配了等同的权重。然而，与普通用户相比，对那些评分与所讨论问题相似的用户给予更多的关注。因此，在前面的模型中，比较合适的方案是为每一个用户分配一个合适的权重系数。数学可以表示为：

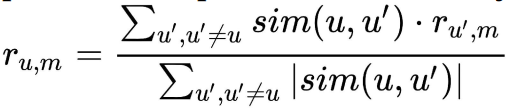
其中，r(u,m)表示为用户u对电影m的评分。对于相似度测量，同样采用余弦距离。

数据处理：将rating表中的NAN替换成0，然后用scikit-learn中的cosine_similarity函数进行处理。

r_matrix_dummy = r_matrix.copy().fillna(0)
r_matrix_dummy.head()
r_matrix_dummy.shape>>> (943, 1647)

from sklearn.metrics.pairwise import cosine_similarity
cosine_sim = cosine_similarity(r_matrix_dummy, r_matrix_dummy)
cosine_sim.shape>>> (943, 943)

# Convert into pandas dataframe
cosine_sim = pd.DataFrame(cosine_sim, index=r_matrix.index, columns=r_matrix.index)
cosine_sim.head()

# User Based Collabrative Filter using Weighted Mean Ratings
def cf_user_wmean(user_id, movie_id):# Check if movie_id exists in r_matrixif movie_id in r_matrix:sim_scores = cosine_sim[user_id]m_ratings = r_matrix[movie_id]idx = m_ratings[m_ratings.isnull()].indexm_ratings = m_ratings.dropna()sim_scores = sim_scores.drop(idx)wmean_rating = np.dot(sim_scores, m_ratings)/ sim_scores.sum()else:#Default to a rating of 3.0 in the absence of any informationwmean_rating = 3.0return wmean_ratingscore(cf_user_wmean)>>> 1.0174483808407588

用户图谱demographics角度考虑

这是一种相对而言更加精细的处理方式。该算法的核心思想是，具有相同图谱的用户倾向于有相似的品味。因此，其有效性取决于这样的假设：女性、青少年或来自同一地区的人在电影选择时会有相同的品味。与前面的模型不同，该种算法不考虑用户对特定电影的评分。相反，算法只关注那些符合特定人群的用户。

3. 基于产品的协同过滤推荐算法实例 Items-based

Items-based和User-based方法本质是一致的，就相当于将第二节中的User变成Item。在基于产品的协同过滤中，我们计算库存中产品的成对相似性。然后，根据user_id和movie_id，计算用户对其所有评分产品的加权平均值。这个模型背后的基本思想是：一个特定的用户可能会对相似的两个产品有相似的评分。

4. 基于模型的方法 Model-based

到目前为止，上面的协同过滤算法被称为memory-based的过滤。因为他们只利用相似性度量来得出结果，并没有从数据中学习任何参数，或者为数据分配类/集群。并没有用到机械学习算法的威力。

以聚类为核心的协同过滤算法 - Clustering

weighted mean-based 的滤波算法，考虑到了每一位用户的评分，最后进行加权；相反，demographic-based滤波算法仅仅考虑了‘某个圈子’的用户，最后进行平均。通常来说，weighted mean-based取得的结果会好于demographic-based，因为考虑的相对来说更广一点。但是，这两种方法仅仅用到了最直接、最粗浅的信息，一种解决方案是进行多维度用户刻画，进行利用机器学习算法解决高纬度数据处理问题。简单说，精准的推荐结果不一定唯一依赖考虑所有用户的感受！

demographic-based算法的缺点来源于他的假设：来自某个相同图谱的用户具有相同的想法和评分。这种极端的思考模式造成了算法的粗浅。Clustering-based方法，如k-means，就是为了改善这种情况：将用户分组到一个群集中，然后在预测评分时只考虑来自同一个群集中的用户。下面以KNN-based clustering为例，构建相关的协同过滤算法。步骤如下 ①找出与用户u对电影m评分最相似的k个最近邻；②输出k个用户对电影m评分的平均值。

可以直接采用Python中的surprise（Simple Python Recommandation System Engine）库实现。Windows 平台下下载方式为：pip install scikit-surprise.

# Import the required classes and methods from the surprise library
from surprise import Reader, Dataset, KNNBasic, evaluate
# Define a Reader object - The Reader object helps in parsing the file or dataframe containing ratings
reader = Reader()
# Create the dataset to be used for building the filter
data = Dataset.load_from_df(ratings, reader)
# Define the algorithm object
knn = KNNBasic()
# Evaluate the performance in terms of RMSE
evaluate(knn, data, measures=['RMSE'])

从输出结果中，我们能够看出来。surprise库将所有的评分数据划分为5个文件包，其中4个文件包用于算法训练，第5个文件包用于模型测试。这样的过程重复了5次。

监督学习和降维方法

对于mxn大小的评分矩阵，每一行代表m个用户中的一个对所有电影的评分；每一列代表n个电影中的一个接受所有用户的评分。前面已经看到了，该评分矩阵是非常稀疏的。通过监督学习的方法，我们可以尝试将这个高度稀疏的矩阵补全。

最简单的思考是，我们可以利用mx(n-1)的评分矩阵进行模型的监督训练，然后对m*1的未知评分进行预测。如此重复n次，那么评分矩阵将有可能完全被填充。理想是丰满的，现实的骨感的。因为，一开始我们用的mx(n-1)的模型训练矩阵就是高度稀疏的~~~（目前也没办法解决这个事，工程上的一种处理手段是用所属的列的均值或中值来填充缺失值，但是考虑到rating矩阵高达90%的系数，计算的均值和中位数一定会引进很大的偏差；同时降维技术，PCA/SVD也不能处理如此稀疏的情况）

可以借鉴的一种思路是，Simon Funk在处理Netflix Problem时，将mx(n-1)的模型训练矩阵压缩到了更低的维度mxd （d << n）,这种处理方式称为SVD-like，其实效果也比较一般。

火极一时的推荐算法-奇异值分解 Singular-value decomposition

本质上，奇异值分解是一种矩阵因子技术，其输入为大型矩阵A，输出为小矩阵U和V。其中，Σ为对角矩阵用于吃调整数据的尺度。对于U矩阵，其实质表征的是用户主成分，英文专有名词对应user-embedding矩阵；V矩阵，其实质表征的是产品主成分，英文专有名词对应item-embedding矩阵。

和大多数机器学习算法一样，传统的SVD矩阵对极其稀疏的评分矩阵是没有效益的。然而，SimonFunk找到了解决这个问题的方法，他的解决方案（SVD++）促成了了推荐系统领域最著名的算法之一。该方法可以利用高度稀疏的评分矩阵A，生成两个非常稠密的user-embedding矩阵U和item-embedding矩阵V。这些稠密的矩阵（U,V）直接解决了原始数据A高度稀疏的难题。surprise库也集成了该算法，调用如下：

#Import SVD
from surprise import SVD
#Define the SVD algorithm object
svd = SVD()
#Evaluate the performance in terms of RMSE
evaluate(svd, data, measures=['RMSE'])