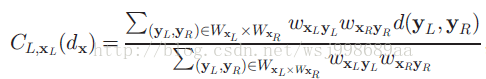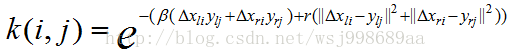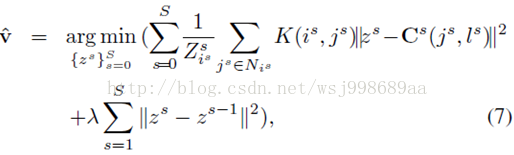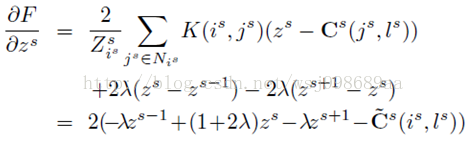最近,在做立体匹配方向相关的研究,先去网上找最新鲜的论文,看到了这篇文献(简称CSCA),来源于CVPR2014,令我惊奇的是,作者竟然提供了详细的源代码,配置运行了一下,效果还真不错,速度也还可以,具有一定的实用价值,所以拿来和大家分享一下。
(转载请注明:http://blog.csdn.net/wsj998689aa/article/details/44411215, 作者:迷雾forest)
1. 立体匹配概念
立体匹配的意思是基于同一场景得到的多张二维图,还原场景的三维信息,一般采用的图像是双目图像,如下所示,第一幅图和第二幅图分别是双目相机得到的左图和右图,第三幅图就是视差图,一看就知道,这就是场景三维图像。
左图 右图 视差图
目前,立体匹配领域,主要有两个评测网站,一个是KITTI(http://www.cvlibs.net/datasets/kitti/eval_stereo_flow.php?benchmark=stereo),另一个是middlebury(http://vision.middlebury.edu/stereo/),两个网站上的算法都交叉,但是又不完全一样,相对来说,KITTI更好一点,对算法的性能评测更好,虽然时间测算的并不准确(CSCA竟然要140s,太离谱了)。
下面说说立体匹配最基本的步骤:
1)代价计算。计算左图一个像素和右图一个像素之间的代价。
2)代价聚合。一般基于点之间的匹配很容易受噪声的影响,往往真实匹配的像素的代价并不是最低。所以有必要在点的周围建立一个window,让像素块和像素块之间进行比较,这样肯定靠谱些。代价聚合往往是局部算法或者半全局算法才会使用,全局算法抛弃了window,采用基于全图信息的方式建立能量函数。
3)深度赋值。这一步可以区分局部算法与全局算法,局部算法直接优化代价聚合模型。而全局算法,要建立一个能量函数,能量函数的数据项往往就是代价聚合公式,例如DoubleBP。输出的是一个粗略的视差图。
4)结果优化。对上一步得到的粗估计的视差图进行精确计算,策略有很多,例如plane fitting,BP,动态规划等。这里不再熬述。
根据我的理解,可以看作为一种全局算法框架,通过融合现有的局部算法,大幅的提高了算法效果。
2. 论文贡献
文献《Cross-Scale Cost Aggregation for Stereo Matching》有三大贡献,第一,设计了一种一般化的代价聚合模型,可将现有算法作为其特例。第二,考虑到了多尺度交互(multi-scaleinteraction),形式化为正则化项,应用于代价聚合(costaggregation)。第三,提出一种框架,可以融合现有多种立体匹配算法。
本文一直强调利用了不同尺度图像“间”的信息,不同于一般的立体匹配算法,只采用了同样尺度下,图像的“内”部结构信息,CSCA利用了多尺度信息,多尺度从何而来?其实说到底,就是简单的对图像进行高斯下采样,得到的多幅成对图像(一般是5副),就代表了多尺度信息。为什么作者会这么提,作者也是从生物学的角度来启发,他说人类就是这么一个由粗到精的观察习惯(coarse-to-line)。生物学好奇妙!
该文献生成的稠密的视差图,基本方法也是逐像素的(pixelwise),分别对每个像素计算视差值,并没有采用惯用的图像分割预处理手段,如此看来运算量还是比较可观的。
3. 算法流程
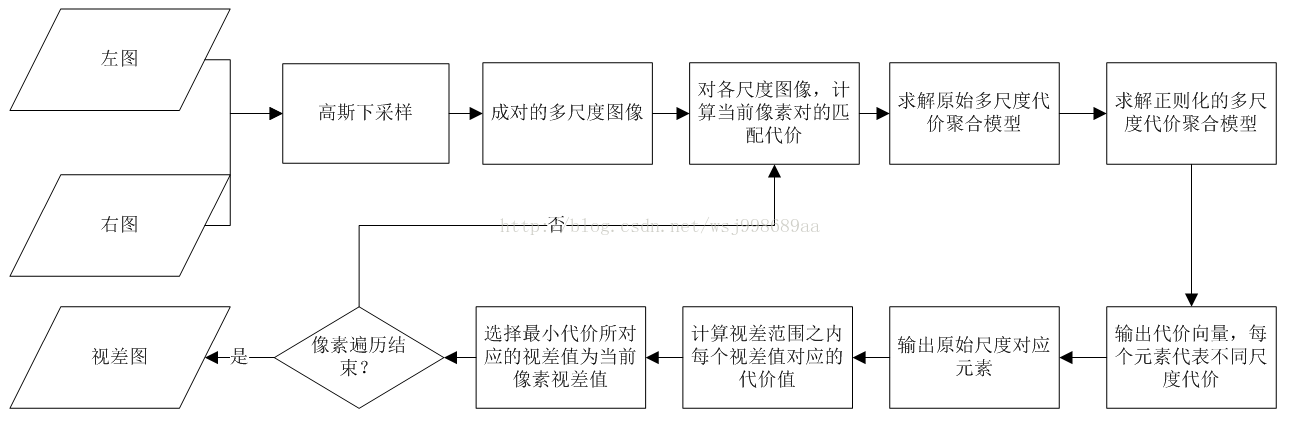
算法流程图如下所示:
其实,这篇文章的论述是很清晰的,上图是我根据自己的理解,画的一份算法流程图,下面我根据这份流程图,对文章脉络进行说明,对关键的公式进行解释。
1. 对左右两幅图像进行高斯下采样,得到多尺度图像。
2. 计算匹配代价,这个是基于当前像素点对的,通常代价计算这一步并不重要,主要方法有CEN,CG,GRD等几种,论文中给出了GRD,公式如下所示:
这个公式同时考虑到了颜色信息与梯度信息,i就是左图中的像素,il就是右图中的对应像素。
3. 匹配代价计算完毕,下一步就是代价聚合了,这也是本文的第一个贡献,文章建立了一个一般化的代价聚合模型,这个模型如下所示:
这个模型,神奇的地方在于,可以融合现有的多种代价聚合算法,比如the-state-of-art的NL,ST,BF,GF等,但是很遗憾,文章没有给出明确的推导公式,用以说明为什么上述代价聚合算法可以作为上述模型的特例,只有一大段的文字描述,缺乏有力的说服力。
解释一下这个一般化模型,它的目的是求解当前像素i的最小匹配代价,l为视差未知变量,j是像素i的邻域内的其他像素,K(i,j)就是像素i,j的相似度,这个相似度可以基于空间信息,也可以基于梯度,颜色信息,不同的核函数,就可以等价于不同的代价聚合算法。从另外一个角度解释一下,为何要z-C(j,l)?我认为这是基于两点假设,一个是左图右图匹配的越好,那么整体代价就越小。另一个是统一邻域内的像素深度值往往差不多。
上述模型的求解很容易,直接对z求偏导即可,形式如下:
这里,我尝试给出一个一般性的简单证明:
在DoubleBP中,所使用的代价函数叫做Birchfield and Tomasi’s pixel dissimilarity,基于它的代价聚合具体形式如下:
对比上面两个公式,很容易看出Zi就是下面公式的分母,也就是权值的均值,刚好和文献表述吻合,而C(j, l)就是d(Yl, Yr),代表的是代价计算函数,核函数的具体形式如下所示,代表的是支持窗口内当前优化像素与其他像素的相似度。
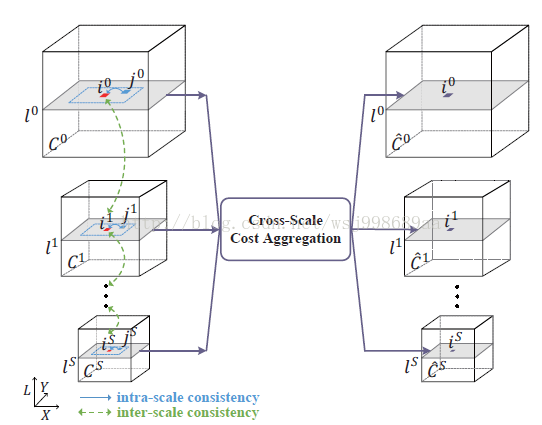
4. 本文的第二个贡献,建立多尺度的代价聚合模型,我们注意上面介绍的模型的邻域N是在原始图像上的,并没有考虑到多尺度信息。 何为多尺度?其实就是不同模糊程度的图像,就好比一个人向你由远到近的走过来,最开始,你肯定只能看到一个模糊的人影,到你面前你就连五官都能看的很清晰了!
多尺度代价聚合模型如下所示:
上面的公式,每一个变量都多了个s,s就代表不同尺度的变量,由于每一项都是一个正数,求解就直接简化为单独对每一个尺度下的对应公式进行求解,如下所示:
5. 建立了多尺度代价模型之后还远远不够,多尺度之间的关系呢?这个必须考虑到啊,于是本文最猛的一个创新点诞生了,作者通过添加正则化项的方式,考了到了多尺度之间的关系,牛逼啊!
我解释一下这个正则化项,请看如下图示:
正则化项的意义在于:保持不同尺度下的,同一像素的代价一致,如果正则化因子越大,说明同一像素不同尺度之间的一致性约束越强,这会加强对低纹理区域的视差估计(低纹理区域视差难以估计,需要加强约束才行),但是副作用是使得其他区域的视差值估计不够精确。不同尺度之间最小代价用减法来体现,L2范式正则化相比较于L1正则化而言,对变量的平滑性约束更加明显,关于这点可以参考我之前的博客(http://blog.csdn.net/wsj998689aa/article/details/39547771)
求解方法也很简单,直接对z求偏导即可,如下:
令偏导等于零,可以建立各个尺度下的线性关系,将各个尺度下的线性关系形式化为矩阵方程形式,很容易得到如下解公式:
6. 得到最小代价公式后,下一步就是将每一个视差值代入上式,选择最小的那个代价对应的视差值为当前像素视差值,这竟然也被称呼为一个算法(winner-takes-all),并且几乎每篇stereo matching文献都要提,感觉瞎扯淡啊。
4. 实验效果
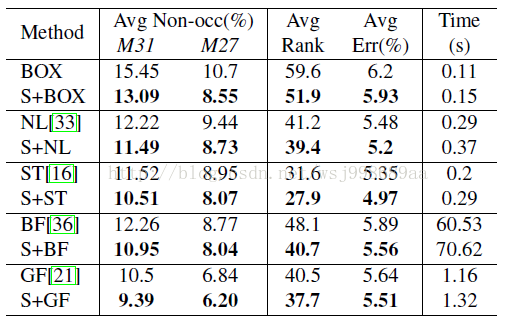
实验效果其实没什么好说的了,大家去看看论文里面就知道了,我直说一点,该文献虽然在middlebury上找不到,但是也的确和middlebury上的算法进行了比较,比如NL,ST,BF,GF等,我也很奇怪,为何middlebury上没有CSCA?
看得出来,算法的效果还是很明显的,我在实际的双目图像上也测试过,效果的确很好。再来说说运行时间,在KITTI评测网站上,CSCA上给出的时间竟然有140s,而最快的算法运行时间只要0.2s!!!这也差距太大了吧,抱着怀疑的态度,我实验了一下,结果发现,在“CEN+ST+WM”组合下,在640p的图像上,运行时间需要6.9s,在320p的图像上,运行时间为2.1s,在160p上,需要0.43s。140s从何而来呢?从上面的表格中也可以看出,S+GF也只需要1.32s,KITTI采用的就是S+GF的组合方式。
5. 总结
1)CSCA是一个优秀的立体匹配算法,它的性价比,综合来说是比较高的,并且CSCA只是一个框架,言外之意,我们可以根据框架的思想自己创建新的算法,说不定能够获取更好的性能。
2) CSCA最可贵的是,提供了详细的源代码,在文献中提示的地址就可以下载到,为作者这种诚实的,敢于开源的精神点赞!
3)我认为CSCA是一个多尺度的局部算法,还不应该归类为全局算法的类别,这种多尺度思想,我想在今后的工作中会有越来越多的研究人员继续深入研究。