本文主要是介绍GIS中非常重要又比较难以理解的坐标系统(地球体、水准面、测量坐标系、地图投影等知识详解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
GIS中非常重要又比较难以理解的坐标系统(地球体、水准面、测量坐标系、地图投影等知识详解)
1、 地球体
1.1 地球球体
地球真实不是一个正球体,而是一个极半径略短、赤道半径略长,北极略突出、南极略扁平,近于梨形的椭球体。

1.2 地球的物理表面
水准面:当海洋静止时,自由水面与该面上各点的重力方向(铅垂线)成正交,这个面则叫做水准面。
大地水准面:在众多水准面中,有一个与静止的平均海水面相重合,并遐想其穿过大陆、岛屿形成一个闭合曲面,这就是大地水准面。换一种说话,大地水准面是一个起伏不平的重力等位面即地球物理表面,它所包围的形体称之为大地体。

2.1 大地水准面的意义
(1) 地球形体的一级逼近
对地球形状的很好近似,其面上高出与面下缺少的相当。
(2)起伏波动在制图学中可忽略
对大地测量和地球物理学有研究价值,但在制图业务中,均把地球当作正球体。
(3)海拔高程的起算面
可使用仪器测得海拔高程—某点到大地水准面的垂直高度,也叫绝对高程,简称高程。关注并星标《测绘之家》微信公众号,可获取更多测量技术干货!
在局部地区,无法知道绝对高程时,假定一个水准面作为高程起算面,地面点到该假定水准面的垂直距离称为相对高程。

HA , HB代表绝对高程,H’A, H’B为相对高程。
1.3 地球的数学表面
在测量和制图中就用旋转椭球体来代替地球体,这个旋转椭球体通常称为地球椭球体,简称椭球体。

椭球体是一个规则的数学表面,所以被视为地球体的数学表面,也是地球形体的二级逼近,用于测量计算的基准面。
决定地球椭球体形状和大小的参数:

举个坐标系的例子来说,WGS84的参数为:
A=6378137m,b=6356752.3m,f=(a-b)/a

对地球形状a,b,f测定后,还必须确定大地水准面与椭球体面的相对关系。即确定与局部地区大地水准面符合最好的一个地球椭球体—参考椭球体,这项工作就是参考椭球体定位。
通过数学方法将地球椭球体摆到与大地水准面最贴近的位置上,并求出两者各点间的偏差,从数学上给出对地球形状的三级逼近。
2、 地球坐标系
2.1 地理坐标系
用经纬度表示地面点位的球面坐标系。在大地测量学中,对于地理坐标系统中的经纬度有三种描述:天文经纬度、大地经纬度、地心经纬度。
天文经纬度:表示地面点在大地水准面上的位置,用天文经度和天文纬度表示。
大地经纬度:表示地面点在参考椭球面上的位置,用大地精度λ,大地纬度ψ,大地高h表示。

地心经纬度:即以地球椭球体质量中心为基点,地心经度通大地经度λ,地心纬度是指参考椭球面上某点和椭球中心连线与赤道面之间的夹角ψ。关注并星标《测绘之家》微信公众号,可获取更多测量技术干货!
在大地测量学中,常以天文经纬度定义地理坐标。在地图学中,以大地经纬度定义地理坐标。
2.2 我国的大地坐标系统
(1)参心坐标系
我们从参心坐标系和地心坐标系来讲解我国的大地坐标系。
参心坐标系是以参考椭球的集合中心为基准的大地坐标系,通常划分为参心空间直角坐标系(x,y, z),参心大地坐标系(B,L,H)。
我国常用的有1954北京坐标系,1980西安坐标系,新1954北京坐标系。
1)1954北京坐标系
原点在前苏联普尔科沃,参考椭球为克拉索夫斯基椭球,主要参数为:a=6378254米,f=1/298.3
2)1980西安坐标系
原点在陕西省泾阳县永乐镇,参考椭球为国际大地测量与地球物理联合会1975年推荐的椭球,主要参数为:
a=6378140米,地球重力场二阶球谐系数J2=1/298.3,引力常数与地球质量的GM=3.986005×1014m3/s2
地球自转角速度w=7.292115×10-5rad/s
3)新1954北京坐标系
1980西安坐标系基础上,将基于IUGG1975年椭球的1980西安坐标系平差成果整体转换为基于克拉索夫斯基椭球的坐标值,并将1980西安坐标系坐标原点空间平移而建立起来的。
(2)地心坐标系
地心坐标系是以地球质心为原点建立的空间直角坐标系,或以球心与地球质心重合的地球椭球面为基准面所建立的大地坐标系。
我们国家使用的地心坐标系有WGS-84坐标系,2000国家大地坐标系。
1) 原点为地球质心M,Z轴指向BIH1984.0定义的协议地极(CTP),X轴指向XMZ平面,且与Z轴、X轴构成右手坐标系。
2) 2000国家大地坐标系(CGCS2000坐标系)
原点为地球质心M,Z轴指向由原点指向历元2000.0的地球参考极的方向,X轴向由原点指向格林尼治参考子午线与赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手坐标系。
(3) 我国的大地控制网
我国的大地控制网是由平面控制网和高程控制网组成。
由精确测定平面位置和高程的典型的具有控制意义的点组成,它是测制地图的基础。
1) 平面控制网
平面控制网采用平面控制测量确定控制点的平面位置,即大地经度和大地纬度,其主要方法是三角测量和导线测量。目前提供使用的国家平面控制网含三角点、导线点154348个,构成1954北京坐标系统、1980西安坐标系两套系统。

2) 高程控制网
由精准测定了高程的地面点组成的控制网,是测定其他地面点高程的基础。建立高程控制网的目的是为了精准求算绝对高程,即高程。中国高程起算面是黄海平均海水面,是根据验潮站确定的多年平均海水面确定的。
我国采用的高程系有两种:1956年黄海高程系和1985年国家高程基准。
1956年黄海高程系,是1956年在青岛观象山设立的水准原点,取1950-1956年共7年的验潮资料,水准原点高程为72.2893米。
1985国家高程标准:取1952年—1979年共28年的验潮资料,水准原点高程为72.2604米。比黄海平均海水面上升了29毫米。1987年国家测绘局公布启用《1985国家高程标准》取代《黄海平均海水面》。

3、 地图投影
3.1 地图投影概述
3.1.1 地图投影的基本问题
地球表面是不可展开的曲面,而地图必须是一个平面,因此将地球表面展开成地图平面必然会产生裂隙或褶皱,必须采用一定的数学方法将曲面展成平面,而且使其变形较小,这种数学方法,成为地图投影。
3.1.2 地图投影的变形
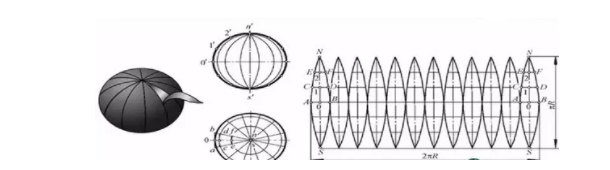
地图投影的变形,通常可以分为长度、面积和角度三种。其中,长度变形是其他变形的基础。
3.1.3 地图投影的分类
地图投影的分类方法很多,总的来说基本可以以外在的特征和内在的性质进行分类。
变形分类:
等角投影:地球表面上无穷小图形投影后仍保持相似,或两微分线段所组成的角度投影后仍保持相似或不变(又称之为正形投影)。
等面积投影:地球表面上的图形在投影前后面积保持不变;
任意投影:既不具备等角性质,又没有等面积性质的投影,统称为任意投影。
等距离投影:在任意投影中,如果沿某一方向的长度比等于1,即a=1或b=1,则这种投影称为等距离投影。

根据投影面分类
首先讲一下投影面
在地图投影中,首先将地球面投影到圆锥、圆柱、平面这些可展的曲面上,然后将这些可展平面沿母线剪开展开成平面,因此相应可得到圆锥投影、圆柱投影和方位投影。
圆柱投影:投影面为圆柱
圆锥投影:投影面为圆锥
方位投影:投影面为平面

根据投影面与地球表面的相关位置分类
投影面位置:
正轴投影:极点在两地极上,或投影面的中心线与地轴一致。
斜轴投影:极点既不在两极上又不在赤道上,或投影面的中心线与地轴斜交。
横轴投影:极点在赤道上,或投影面的中心线与地轴垂直。

3.2 我国地理信息系统中地图投影的应用
我国的各种地理信息系统中采用了我国基本比例尺地形图一直的地图投影系统,即大于等于1:50万的地形图,采用高斯-克吕格投影;小于1:50万的地形图采用正轴等角割圆锥投影(又称兰伯特投影)。
高斯-克吕格投影是一种等角横切椭圆柱投影。我们把地球看成是地球椭球体,假想,用一个椭圆筒套在其上,使筒与地球椭球体的某一经线相切,椭圆筒与地球椭球体的某一经线相切,椭圆筒的中心轴位于赤道上,按等角条件将地球表面投影到椭圆筒上,然后将椭圆筒展开成平面,这就是高斯投影。
这篇关于GIS中非常重要又比较难以理解的坐标系统(地球体、水准面、测量坐标系、地图投影等知识详解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




