分治算法——912. 排序数组

本文主要是介绍分治算法——912. 排序数组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

• • 🍈1. 题目
  • 🍌2. 算法原理
  • 🍏3. 代码实现

🍈1. 题目

题目链接：912. 排序数组 - 力扣（LeetCode）

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

• 1 <= nums.length <= 5 * 104
• -5 * 104 <= nums[i] <= 5 * 104

🍌2. 算法原理

如果不讲武德，直接sort排序，然后返回，这样也是能通过的，但是意义不大

我们当然是选择用分治的思想，自己来实现这个快排。

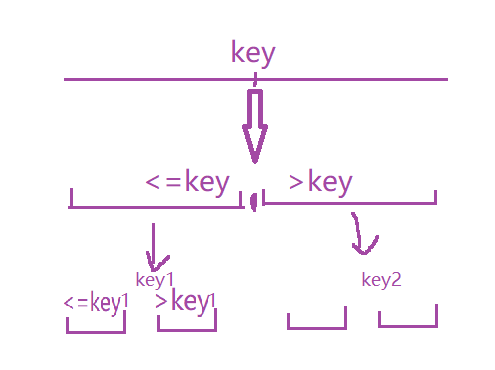
这里简单讲解一下快排（以升序为例）：

给一个数组，选定一个基准元素key，然后根据这个基准元素，将这个数组分为两部分：

• key左边这个区间的元素全都是小于等于>= key
• key右边的区间的元素全都是< key的

接下来再将从左边的区域选取基准值、右边的区域选取基准值，依此重复这个操作

这就是快排的核心思想。

不过这个的缺陷就是对应有着大量重复元素时，时间复杂度会退化到O(N²)

所以此题采用的是三路划分的思想，来实现快排

建议先看看此篇文章——分治算法——75. 颜色分类，思想一样

我们将数组分为三个区域，即：

1. 小于key：< key
2. 等于key：== key
3. 大于key：> key

和上面这个75.颜色分类题目同理，三个指针：left、right、i，这里分类套路三种情况

1. nums[i] < key：swap(nums[++left] , nums[i++])
2. nums[i] == key：i++
3. nums[i] > key：swap(nums[--right] , nums[i])

为什么三路划分效率会高一点：

如果这个数组里面全都是key的时候，我们经过一次数组划分，中间这些元素全都是等于key的，接下来中间区域的元素不用管，去左右区间，但此时左右区间并不存在，直接退出递归，所以此时的复杂度从O(N²)降到了O(N)

优化——如何选取key值：

如果要将快排的时间复杂度将近为Nlog(N)，要采用随机选key（大佬证明过），有兴趣的可以查阅《算法导论》这本书。

GPT回答(稍微看一下)：
快速排序的时间复杂度分析涉及到分割的效率和基准值选择对数组分割的影响。
分割的效率：快速排序的性能高度依赖于数组分割的均匀性。理想情况下，每次分割都能将数组几乎均匀地划分成两个子数组。随机选择基准值可以增加分割的随机性，从而在平均情况下更有可能实现近似均匀的数组分割，进而提高算法的效率。
避免最坏情况：最坏情况下的时间复杂度为 O(N²)，这种情况通常发生在基准值的选择不当时，例如每次都选择最大或最小的元素作为基准值。随机选择基准值能够降低最坏情况发生的概率，因为在随机选择的情况下，每次都选取最大或最小值的概率较低。
期望的平均情况：随机选择基准值能够增加算法在平均情况下的效率。数学上的期望证明表明，随机选择基准值导致数组被分割成近似相等的两部分的概率较高，因此排序的时间复杂度在平均情况下接近于 O(N*logN)。
综上所述，随机选择基准值有助于提高快速排序的效率。它增加了分割的随机性，降低了最坏情况发生的概率，并在平均情况下实现了更好的性能，使得时间复杂度接近于 O(N*logN)。这种随机性导致平均情况下更为均衡的分割，从而提高了整体排序的效率。

🍏3. 代码实现

class Solution {
public:vector<int> sortArray(vector<int>& nums){srand(time(NULL));  //s->start  rand->randomquickSort(nums,0,nums.size()-1);return nums;}void quickSort(vector<int>& nums, int l, int r){if(l >= r)  return;//三路划分int key = getRandom(nums,l,r);int i = l, left = l -1, right =r + 1;while(i < right){if(nums[i] < key)   swap(nums[++left],nums[i++]);else if(nums[i] > key)  swap(nums[--right],nums[i]);else    i++;}//划分完之后继续划分quickSort(nums,l,left);quickSort(nums,right,r);}int getRandom(vector<int>& nums, int left, int right){int r = rand();return nums[r%(right - left + 1) + left];}};

---

对排序不是和了解的，可以查看此篇文章：七大排序

这篇关于分治算法——912. 排序数组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---