本文主要是介绍Keras入门笔记(番一):从源码分析K.batch_dot及与dot的区别,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
动机
矩阵和向量的乘法各种名称都有,甚至相互混杂,在不同框架里的命名也不一样,每每都会陷入这些Magic中。例如,同样是dot对向量shape= (n,)和一维张量shape=(n,1)而言都不一样,无论总结过多少次,像我们这种torch和tensowflow、matlab轮着写的人,总是不经意间就会翻车。
好在keras提供了高级的接口,至少在tensorflow、theano以及可能会有的mxnet上的表现是一致的。
各种向量乘法的命名
我个人非常烦什么“点积、外积、内积、点乘、叉乘、直积、向量积、张量积”的说法,乱的不行。我觉得,还是应该统一一下,别一会儿点积一会儿点乘,二维一维都不区分,非常容易乱。由于中文教材各种翻译都有,因此主要还是用wiki作为统一吧。
一维(向量)
- 需要注意的是,
shape=(n, )的才是一维向量,shape(n,1)已经变成张量了。
- Dot product
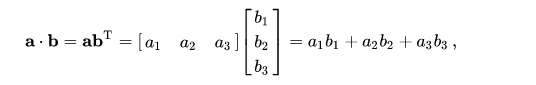
import numpy as np
a = np.array([1,2,3,4,5]) # 向量,不区分列向量或行向量。应该视为列向量。
b = a.reshape((5,1)) # 张量
print(a.shape, b.shape, a.T.shape) # (5,) (5, 1) (5,)
print((a+b).shape) # (5, 5)
print(np.dot(a,a), a*a) # 55 [1 4 9 16 25]
print(np.dot(b.T,b)) # [[55]]
# Also, a*a = np.multiply(a, a), b*b = np.multiply(b, b)
- Cross product
构建神经网络时基本不用,仅在工程优化中大量使用,如共轭梯度等。API一般为
cross(a, b)。
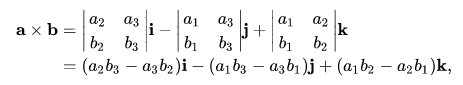
- element-wise
逐元素乘法,也就是 Dot product 不进行求和: c i = a i b i c_i=a_ib_i ci=aibi。API一般为
multiply(a, b)
二维(矩阵)
- Hadamard product
常说的对应元素逐元素相乘。也是element-wise的一种。API一般是
multiply(a, b)。
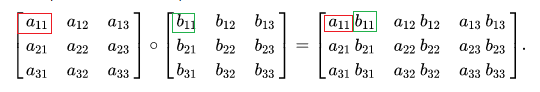
- Matrix multiplication
就是线代中的矩阵乘法。一般也由
dot(a, b)或matmul(a, b)
这篇关于Keras入门笔记(番一):从源码分析K.batch_dot及与dot的区别的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



