本文主要是介绍【MATLAB】EWT分解+FFT+HHT组合算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~
1 基本定义
EWT+FFT+HHT组合算法是一种广泛应用于信号处理领域的算法,它结合了经验小波变换(Empirical Wavelet Transform,EWT)、快速傅里叶变换(Fast Fourier Transform,FFT)和希尔伯特黄变换算法(Hilbert-Huang Transform,HHT)的优点,具有较高的计算效率和准确性。
-
经验小波变换(EWT):EWT是一种基于数据自适应的信号分解方法,它通过分析信号的局部特征来选择合适的小波基进行信号分解。与传统的固定小波基不同,EWT能够更好地适应不同类型的信号,并提供更准确的分解结果。
-
快速傅里叶变换(FFT):FFT是一种高效计算离散傅里叶变换(DFT)的算法,它能够快速计算信号在频域上的表示。通过将信号从时域转换到频域,我们可以更好地理解信号的频率成分和特征。
-
希尔伯特黄变换算法(HHT):HHT是一种用于非线性和非平稳信号处理的算法,它通过经验模式分解(Empirical Mode Decomposition,EMD)将信号分解为一系列固有模式函数(Intrinsic Mode Functions,IMF),然后对每个IMF进行希尔伯特谱分析,得到信号的时频分布和能量特征。
在 EWT+FFT+HHT 组合算法中,首先使用 EWT 对信号进行自适应分解,得到一系列本征模函数(Intrinsic Mode Functions,IMF);然后对每个 IMF 进行 FFT 计算其频谱特征;最后使用 HHT 对每个 IMF 进行希尔伯特谱分析,得到信号的时频分布和能量特征。这种组合算法能够充分利用三种方法的优点,具有较高的计算效率和准确性,适用于各种类型的信号处理任务。
除了上述提到的优点,EWT+FFT+HHT组合算法还具有以下特点:
-
自适应性:EWT能够根据信号的局部特征自适应地选择合适的小波基进行信号分解,从而更好地适应不同类型的信号。
-
高效性:FFT是一种快速计算离散傅里叶变换的算法,能够高效地计算信号的频域表示。HHT在处理非线性和非平稳信号时具有较高的计算效率。
-
非线性分析能力:HHT能够处理非线性和非平稳信号,通过EMD将信号分解为IMF,然后对每个IMF进行希尔伯特谱分析,得到信号的时频分布和能量特征。
-
多尺度分析能力:EWT和HHT都具有多尺度分析能力,能够同时在不同的尺度上分析信号的局部和全局特征。
-
广泛适用性:EWT、FFT和HHT都是广泛适用于各种类型的信号处理任务,包括但不限于信号去噪、特征提取、异常检测、时间序列分析等。
总之,EWT+FFT+HHT组合算法是一种非常强大的信号处理工具,它结合了三种方法的优点,具有自适应性、高效性、非线性分析能力和多尺度分析能力等特点,适用于各种类型的信号处理任务。
EWT+FFT+HHT组合算法还有一些其他的特性和优势。
-
鲁棒性:由于EWT、FFT和HHT都是基于数据的方法,它们对噪声和异常值具有较强的鲁棒性。即使在存在噪声和异常值的情况下,这些方法也能够得到较好的结果。
-
多域分析能力:EWT和FFT能够在时域和频域上进行分析,而HHT则能够在时频域上进行分析。因此,EWT+FFT+HHT组合算法具有多域分析能力,能够提供更全面的信号特征。
-
跨领域应用:由于EWT、FFT和HHT都具有广泛的应用领域,因此EWT+FFT+HHT组合算法也具有跨领域应用的能力。它可以应用于各种不同的领域,包括但不限于医学图像处理、地震信号处理、金融时间序列分析等。
-
可解释性:相对于一些黑箱机器学习方法,EWT+FFT+HHT组合算法具有较好的可解释性。使用者可以理解算法的每个步骤和原理,从而更好地解释结果和做出决策。
综上所述,EWT+FFT+HHT组合算法是一种非常强大的信号处理工具,它具有自适应性、高效性、非线性分析能力、多尺度分析能力和鲁棒性等特点,适用于各种类型的信号处理任务,并具有广泛的应用前景。
2 出图效果
附出图效果如下:

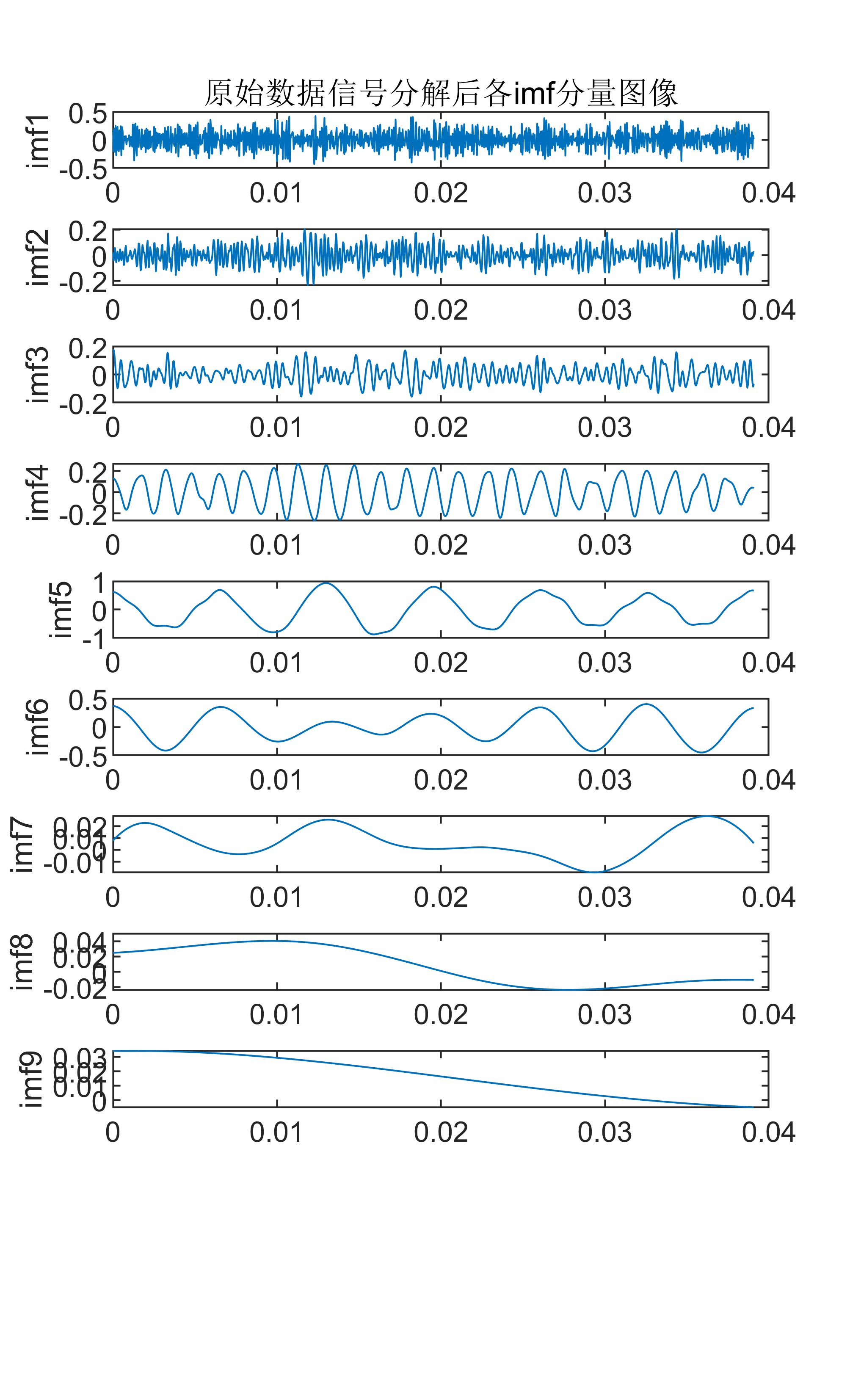


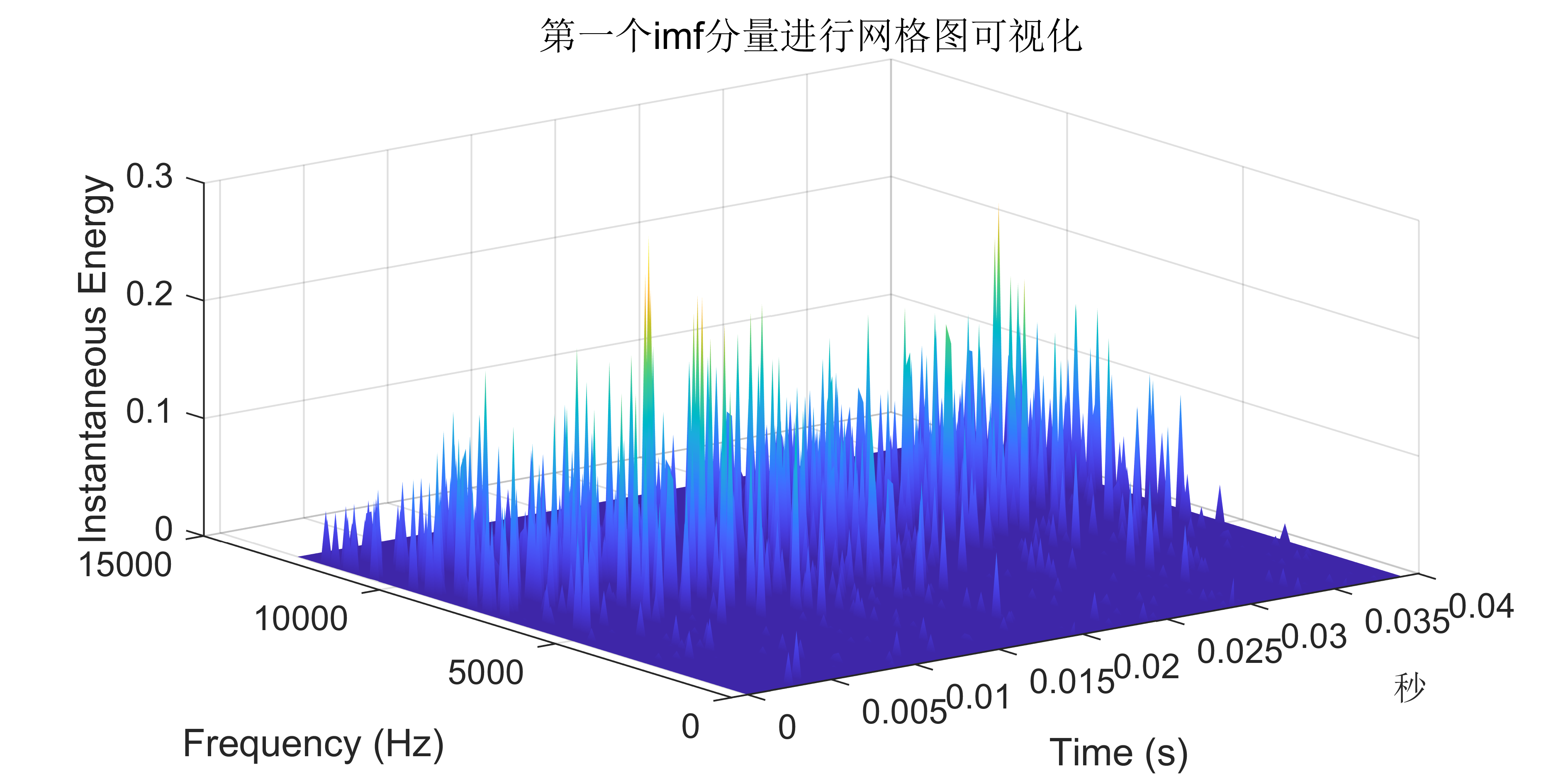
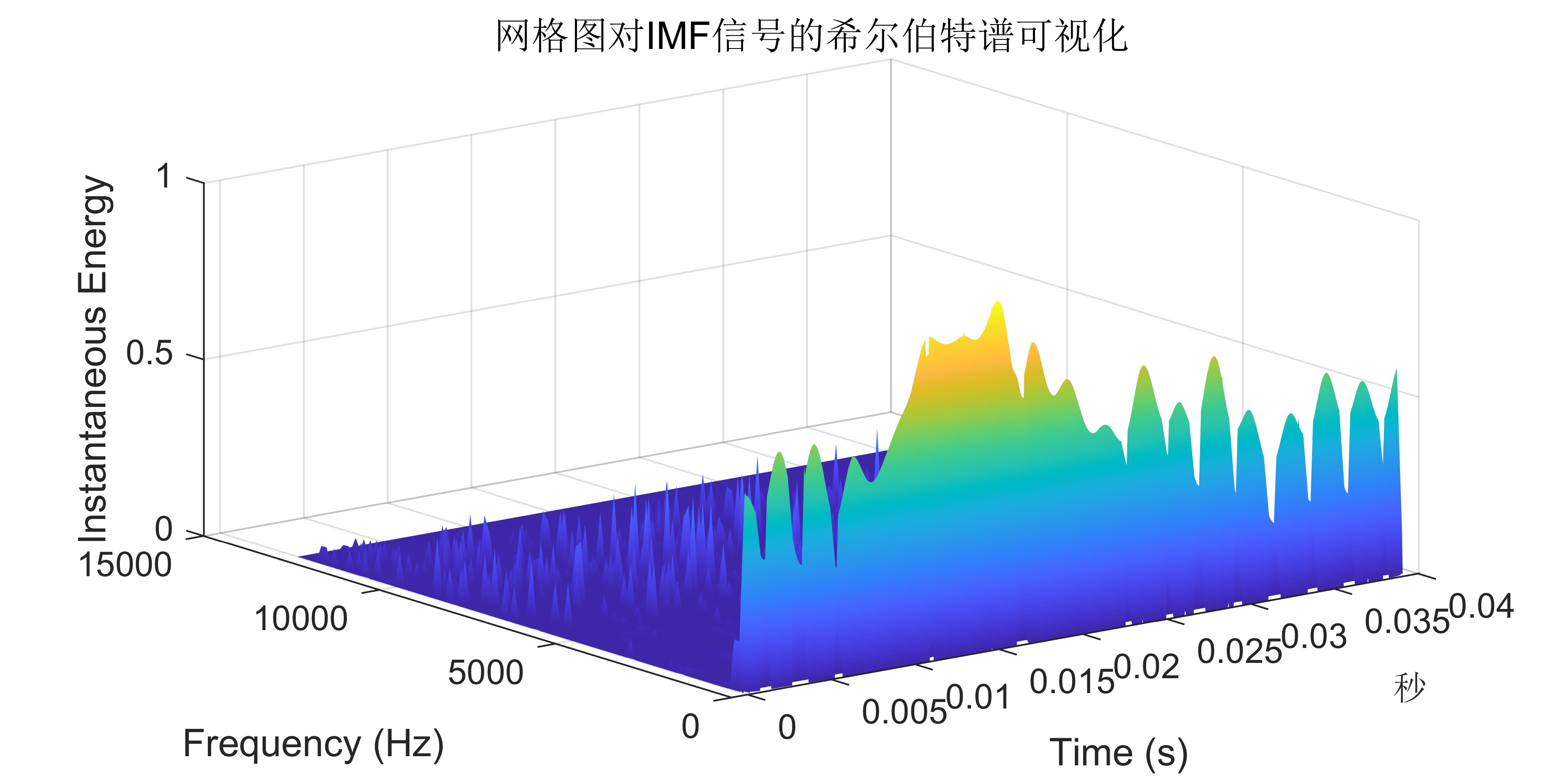
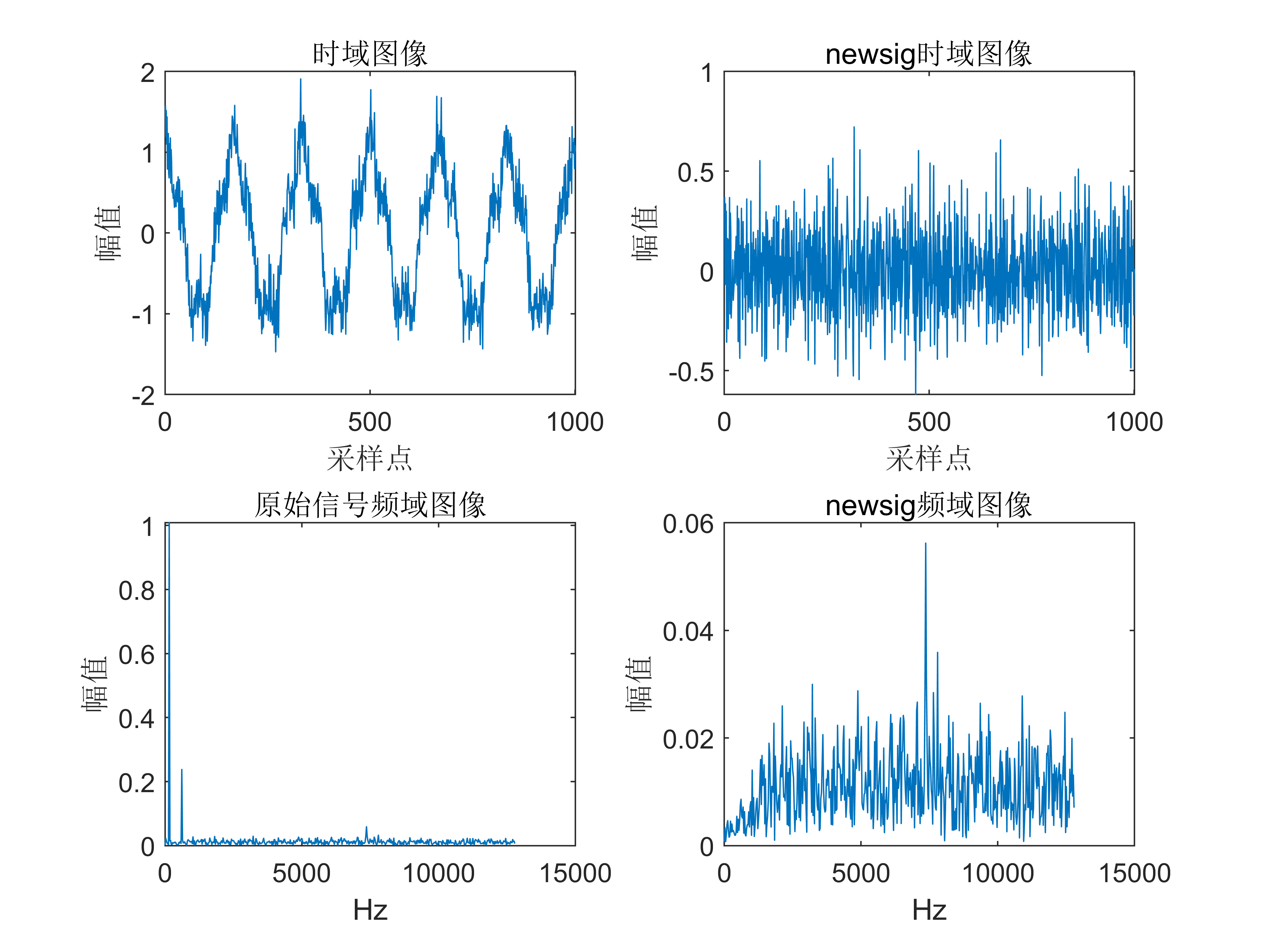
附视频教程操作:
【MATLAB】EWT分解+FFT+HHT组合算法
这篇关于【MATLAB】EWT分解+FFT+HHT组合算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









