本文主要是介绍【算法每日一练]-图论(保姆级教程篇9 最小生成树 ,并查集篇)#道路修建 #兽径管理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
题目:道路修建
思路:
题目:兽径管理
思路:
题目:道路修建



思路:
“让这些点全部连在一起的最小代价”很明显是最小生成树。绝对不能kruskal,存边一定会超内存。所以只能prim。
但是这些点之间的边我们还是不能存,最好的方式就是一边建树一边计算距离。
因为我们每次都要取距离集合最小的点,那么我们就要维护一个dis数组。
思路是这样的:
集合中的点到集合距离一定是0,
集合外的点到集合的距离一定需要与集合中的每个点的距离进行比较取最小值。
但是如果说集合每变动一次,集合外的点就把集合中的点全部遍历一遍非常没必要。
因为之前已经比较过的点根本就不用再比较,基于这个思想。
我们完全可以在集合中每个元素进入集合的时候进行比较就行,这样相当于是把新进入集合的元素要和集合外的所有元素进行距离更新即可
计算方式为:dis[j]=min(dis[j],cur到j的距离)
#include <bits/stdc++.h>
using namespace std;
int n,cnt;
double sum;
int vis[5005];
double dis[5005],x[5005],y[5005];//dis是每个点到集合的最小距离double cal(double x1,double y1,double x2,double y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
void prim()
{dis[1]=0;vis[1]=1;for(int i=1;i<=n;i++){//一共要n个点全部进入集合int cur=1;double minn=1e9*1.0;for(int j=1;j<=n;j++)if(!vis[j]&&dis[j]<minn){//获取最近点minn=dis[j];cur=j;}vis[cur]=1;sum+=dis[cur];for(int j=1;j<=n;j++){if(!vis[j])dis[j]=min(dis[j],cal(x[cur],y[cur],x[j],y[j]));}}printf("%.2lf",sum);
}int main()
{cin>>n;for(int i=1;i<=n;i++){scanf("%lf%lf",&x[i],&y[i]);;//输入每个点的坐标dis[i]=1e12*1.0;}prim();
}
题目:兽径管理


思路:
这么长的题你应该也不会读,我捋一下:
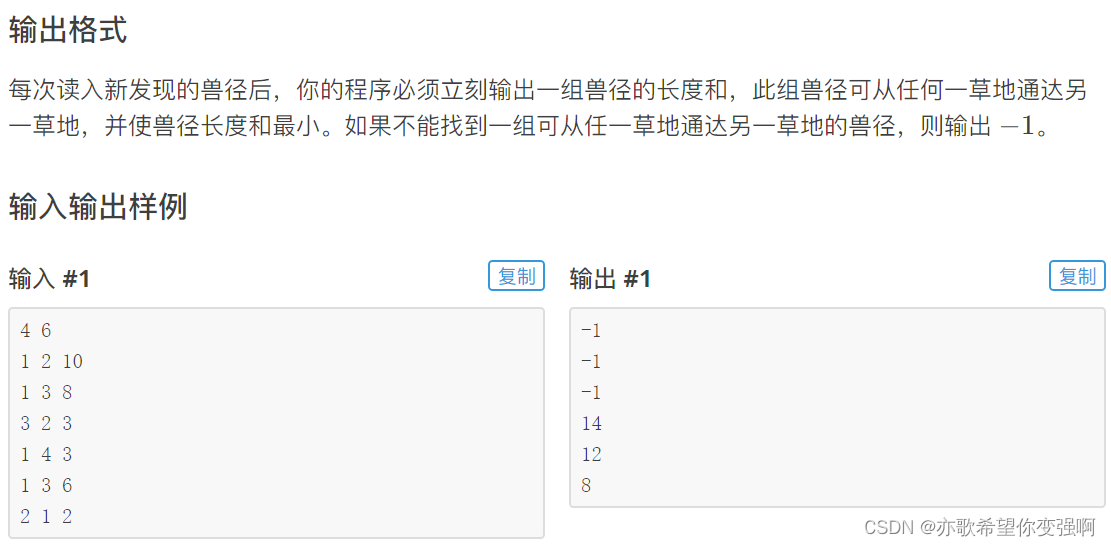
牛群希望能够在任意两块草地间移动,草地编号1~n,共w周牛群每周发现一个新路,输出每周任意两块草地路径总和,如果不能到达就输出-1。
这道题本来不难的,我花了一下午找bug,结果发现又tm在排序上犯老毛病了!(原数组是有序的)别学我啊
原来的边是按照时间顺序的,现在一排序就不知道原来的出现时间了,那么就需要增加一个id记录出现时间,也是边原来的标号。
第一种解法是每周跑一次,kruskal时间晚于本周的边不统计
第二种解法是倒着进行kruskal。在最后一周跑的kruskal上统计用到的边,每往前一周删一条边,如果这条边没有被用到,那么使用上个结果,否则重跑。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=205,M=6005;
int f;
struct Edge{ int u,v,w,id; }e[M];
int fa[N],n,m;
int use[M],vis[M];//vis表示被删掉的边,use表示在上次结果中被用到的边
ll ans[M];bool cmp(Edge a,Edge b){ return a.w<b.w;}void init(){for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集节点memset(use,0,sizeof(use));
}
int find(int x)
{if(x!=fa[x]) fa[x]=find(fa[x]);return fa[x];//返回祖先
}ll kruskal()
{init();ll tmp=0;int cnt=0;for(int i=1;i<=m;i++){if(vis[e[i].id])continue;//此边要判断边的id是否已经被删掉了int fu=find(e[i].u), fv=find(e[i].v);if(fu==fv) continue; //若出现两个点已经联通了,则说明这一条边不需要了tmp+=e[i].w; //将此边权计入答案use[e[i].id]=1;//对id标记fa[fv]=fu; //合并操作if(++cnt==n-1)break;}return cnt==n-1?tmp:-1;
}int main()
{cin>>n>>m;for(int i=1;i<=m;i++){scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);e[i].id=i;//记录边的id号}sort(e+1,e+1+m,cmp);//将边的权值排序ans[m]=kruskal();for(int i=m-1;i>0;i--){//从id开始删边,倒着删边嘛vis[i+1]=1;//对id号删除if(use[i+1]) ans[i]=kruskal();//id被用过else ans[i]=ans[i+1];if(ans[i]==-1){for(int j=1;j<i;j++) ans[j]=-1;break;}}for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';return 0;
}这篇关于【算法每日一练]-图论(保姆级教程篇9 最小生成树 ,并查集篇)#道路修建 #兽径管理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




