本文主要是介绍Plotting Logarithmic Error Bars(如何在log log plot中绘制误差条),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Suppose that one has a sufficient number of measurements to make an estimate of a measured quantity y y y and report its absolute error, ± δ y \pm\delta y ±δy. The absolute error ± δ y \pm\delta y ±δy is represented on a Cartesian plot by extending lines of the appropriate size above and below the point y y y.

If plotted on a logarithmic plot, however, absolute error bars that are symmetric on a y y y vs. x x x plot become asymmetric; the lower portion is longer than the upper portion.
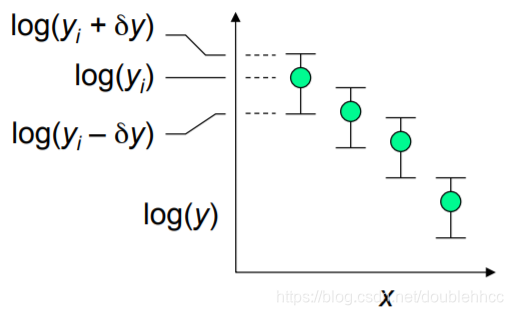
This gives a misleading view of measurement precision, especially when measured quantities vary by several orders of magnitude. To represent error bars correctly on a log plot, one must recognize that the quantity being plotted, which we call z z z, is different than the measured quantity y y y. z = log ( y ) z=\log(y) z=log(y) The error δ z \delta z δz is δ z = δ [ log y ] \delta z=\delta[\log y] δz=δ[logy] On the assumption of small errors, a differential analysis can be used δ z ≈ d z = d [ log 10 e ⋅ ln y ] ≈ 0.434 δ y y \delta z\approx dz=d[\log_{10}e \cdot\ln y]\approx0.434\frac{\delta y}{y} δz≈dz=d[log10e⋅lny]≈0.434yδy The error δ z \delta z δz is thus given by the relative error in y y y: δ z ≈ 0.434 δ y y \delta z\approx 0.434\frac{\delta y}{y} δz≈0.434yδy The error bars now display correctly on a logarithmic plot.

Reference: https://faculty.washington.edu/stuve/log_error.pdf
这篇关于Plotting Logarithmic Error Bars(如何在log log plot中绘制误差条)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








