K近邻算法经典案例实现之海伦约会

2023-11-30 11:40
文章标签 算法 实现 经典 案例 约会 海伦 近邻

本文主要是介绍K近邻算法经典案例实现之海伦约会，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

引言

  上文实现了简单的K近邻算法，本文来介绍下完整的K近邻算法，将实际需求与算法进行结合，做个小小的demo,毕竟'talk is cheap,show me the code.'。

K近邻算法的一般流程如下：

  1. 收集数据：可以使用爬虫进行数据的收集，也可以使用第三方提供的免费或收费的数据。一般来讲，数据放在txt文本文件中，按照一定的格式进行存储，便于解析及处理。
  2. 准备数据：使用Python解析、预处理数据。
  3. 分析数据：可以使用很多方法对数据进行分析，例如使用Matplotlib将数据可视化。
  4. 测试算法：计算错误率。
  5. 使用算法：错误率在可接受范围内，就可以运行k-近邻算法进行分类

案例需求分析

海伦女士一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的任选，但她并不是喜欢每一个人。经过一番总结，她发现自己交往过的人可以进行如下分类：

  1. 不喜欢的人
  2. 魅力一般的人
  3. 极具魅力的人

海伦收集约会数据已经有了一段时间，她把这些数据存放在文本文件datingTestSet.txt中，每个样本数据占据一行，总共有1000行。datingTestSet.txt数据下载： 数据集下载

海伦收集的样本数据主要包含以下3种特征：

  1. 每年获得的飞行常客里程数

  2. 玩视频游戏所消耗时间百分比

  3. 每周消费的冰淇淋公升数

代码实现

数据解析以及可视化
  因为原始数据往往不方便进行直接计算，因此需要对文件进行简单处理成我们需要的数据。可视化是为了方便直接观察数据的规律。

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines# 数据预处理
def fileRead(fileName):#打开文件fr = open(fileName)#读取全部内容arraryOfLines = fr.readlines()#求行数numberOfLines = len(arraryOfLines)#生成numberOfLines行,3列的矩阵，方便后面存放数据returnMat = np.zeros((numberOfLines, 3))#用于存放类别classLabelVector = []#设置索引,用于循环index = 0#开始循环读取for line in arraryOfLines:#去除掉文件中的多余字符line = line.strip()#用空格对内容进行分割listFormLine = line.split('\t')#赋值returnMat[index, :] = listFormLine[0:3]#对类别数组进行赋值if listFormLine[-1] == 'didntLike':classLabelVector.append(1)if listFormLine[-1] == 'smallDoses':classLabelVector.append(2)if listFormLine[-1] == 'largeDoses':classLabelVector.append(3)index += 1return returnMat, classLabelVector# 数据展示
def showData(datingDataMat, datingLabels):fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13, 8))LabelsColors = []for i in datingLabels:if i == 1:LabelsColors.append('black')if i == 2:LabelsColors.append('orange')if i == 3:LabelsColors.append('red')axs[0][0].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 1], color=LabelsColors, s=15, alpha=.5)axs0_title_text = axs[0][0].set_title('flight_play')axs0_xlabel_text = axs[0][0].set_xlabel('flight_time')axs0_ylabel_text = axs[0][0].set_ylabel('play_time')plt.setp(axs0_title_text, size=9, weight='bold', color='red')plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')axs[0][1].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)# 设置标题,x轴label,y轴labelaxs1_title_text = axs[0][1].set_title('flight_eat')axs1_xlabel_text = axs[0][1].set_xlabel('flight')axs1_ylabel_text = axs[0][1].set_ylabel('eat')plt.setp(axs1_title_text, size=9, weight='bold', color='red')plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')# 画出散点图,以datingDataMat矩阵的第二(玩游戏)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5axs[1][0].scatter(x=datingDataMat[:, 1], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)# 设置标题,x轴label,y轴labelaxs2_title_text = axs[1][0].set_title('play_eat')axs2_xlabel_text = axs[1][0].set_xlabel('play_time')axs2_ylabel_text = axs[1][0].set_ylabel('eat_weight')plt.setp(axs2_title_text, size=9, weight='bold', color='red')plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')# 设置图例didntLike = mlines.Line2D([], [], color='black', marker='.',markersize=6, label='didntLike')smallDoses = mlines.Line2D([], [], color='orange', marker='.',markersize=6, label='smallDoses')largeDoses = mlines.Line2D([], [], color='red', marker='.',markersize=6, label='largeDoses')# 添加图例axs[0][0].legend(handles=[didntLike, smallDoses, largeDoses])axs[0][1].legend(handles=[didntLike, smallDoses, largeDoses])axs[1][0].legend(handles=[didntLike, smallDoses, largeDoses])# 显示图片plt.show()fileName = 'datingTestSet.txt'
datingDataMat, datingLabels = fileRead(fileName)
print("datingLabels is",datingLabels)
print("datingDataMat is",datingDataMat)
showData(datingDataMat,datingLabels)

效果展示

类别矩阵以及初始数据矩阵

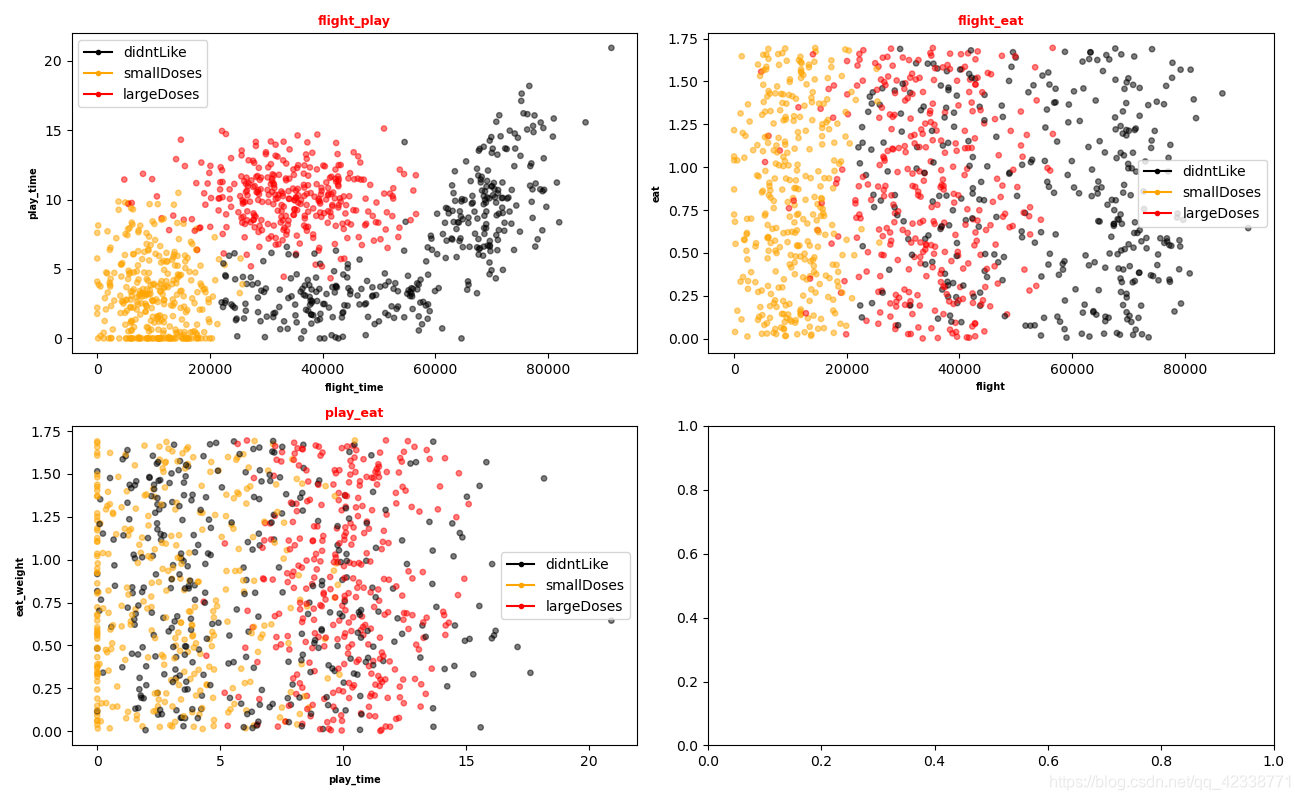
在这里插入图片描述

散点图

在这里插入图片描述

数据归一化

数据为什么要归一化？

  通过上面的图片我们不难发现一个问题，飞行里程数的数据一般都是成百上千，但是吃冰淇淋的总量也就几升而已,这显然会影响欧式距离公式的计算结果，
就如我们小时候画直角坐标系的时候，如果x轴y轴数值差距过大，我们往往会为x,y轴设立不同的比例，以此来让数据更加规整，那是显示层面的，同理
为了让欧式距离公式计算更加精准，我们常用的方法一般为数值归一化，将取值范围取到0到1或者-1到1之间。

归一化公式如下：
n e w V a l u e s = ( o l d V a l u e − m i n ) / ( m a x − m i n ) newValues =(oldValue - min)/(max - min) newValues=(oldValue−min)/(max−min)
代码实现：

def autoNorm(dataSet):#获得数据的最小值minVals = dataSet.min(0)maxVals = dataSet.max(0)#最大值和最小值的范围ranges = maxVals - minVals#shape(dataSet)返回dataSet的矩阵行列数normDataSet = np.zeros(np.shape(dataSet))#返回dataSet的行数m = dataSet.shape[0]#原始值减去最小值normDataSet = dataSet - np.tile(minVals, (m, 1))#除以最大和最小值的差,得到归一化数据normDataSet = normDataSet / np.tile(ranges, (m, 1))#返回归一化数据结果,数据范围,最小值return normDataSet, ranges, minVals

测试算法性能:验证分类器

  机器学习算法的一个重要部分就是对算法进行评估，在监督学习中，通常我们将90%的样本作为训练样本来训练分类器，10%的样本用来测试分类器的准确率。
算法上一期已经实现过，这里就不多赘诉了，直接上完整代码。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import operator# 数据预处理
def fileRead(fileName):# 打开文件fr = open(fileName)# 读取全部内容arraryOfLines = fr.readlines()# 求行数numberOfLines = len(arraryOfLines)# 生成numberOfLines行,3列的矩阵，方便后面存放数据returnMat = np.zeros((numberOfLines, 3))# 用于存放类别classLabelVector = []# 设置索引,用于循环index = 0# 开始循环读取for line in arraryOfLines:# 去除掉文件中的多余字符line = line.strip()# 用空格对内容进行分割listFormLine = line.split('\t')# 赋值returnMat[index, :] = listFormLine[0:3]# 对类别数组进行赋值if listFormLine[-1] == 'didntLike':classLabelVector.append(1)if listFormLine[-1] == 'smallDoses':classLabelVector.append(2)if listFormLine[-1] == 'largeDoses':classLabelVector.append(3)index += 1return returnMat, classLabelVector# 数据展示
def showData(datingDataMat, datingLabels):fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13, 8))LabelsColors = []for i in datingLabels:if i == 1:LabelsColors.append('black')if i == 2:LabelsColors.append('orange')if i == 3:LabelsColors.append('red')axs[0][0].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 1], color=LabelsColors, s=15, alpha=.5)axs0_title_text = axs[0][0].set_title('flight_play')axs0_xlabel_text = axs[0][0].set_xlabel('flight_time')axs0_ylabel_text = axs[0][0].set_ylabel('play_time')plt.setp(axs0_title_text, size=9, weight='bold', color='red')plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')axs[0][1].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)# 设置标题,x轴label,y轴labelaxs1_title_text = axs[0][1].set_title('flight_eat')axs1_xlabel_text = axs[0][1].set_xlabel('flight')axs1_ylabel_text = axs[0][1].set_ylabel('eat')plt.setp(axs1_title_text, size=9, weight='bold', color='red')plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')# 画出散点图,以datingDataMat矩阵的第二(玩游戏)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5axs[1][0].scatter(x=datingDataMat[:, 1], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)# 设置标题,x轴label,y轴labelaxs2_title_text = axs[1][0].set_title('play_eat')axs2_xlabel_text = axs[1][0].set_xlabel('play_time')axs2_ylabel_text = axs[1][0].set_ylabel('eat_weight')plt.setp(axs2_title_text, size=9, weight='bold', color='red')plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')# 设置图例didntLike = mlines.Line2D([], [], color='black', marker='.',markersize=6, label='didntLike')smallDoses = mlines.Line2D([], [], color='orange', marker='.',markersize=6, label='smallDoses')largeDoses = mlines.Line2D([], [], color='red', marker='.',markersize=6, label='largeDoses')# 添加图例axs[0][0].legend(handles=[didntLike, smallDoses, largeDoses])axs[0][1].legend(handles=[didntLike, smallDoses, largeDoses])axs[1][0].legend(handles=[didntLike, smallDoses, largeDoses])# 显示图片plt.show()# 数据归一化
def autoNorm(dataSet):minVals = dataSet.min(0)maxVals = dataSet.max(0)ranges = maxVals - minValsnormalDataSet = np.zeros(np.shape(dataSet))m = dataSet.shape[0]normalDataSet = dataSet - np.tile(minVals, (m, 1))normalDataSet = normalDataSet / np.tile(ranges, (m, 1))return normalDataSet, ranges, minVals#分类器
def classify(input, dataSet, labels, k):# numpy中的shape方法用于计算形状 eg: dataSet: 4*2# print(dataSet.shape)dataSetSize = dataSet.shape[0]# numpy中的tile方法,用于对矩阵进行填充# 将inX矩阵填充至与dataSet矩阵相同规模,后相减diffMat = np.tile(input, (dataSetSize, 1)) - dataSet# 平方sqDiffMat = diffMat ** 2# 求和sqDistance = sqDiffMat.sum(axis=1)# 开方distance = sqDistance ** 0.5# argsort()方法进行直接排序sortDist = distance.argsort()classCount = {}for i in range(k):# 取出前k个元素的类别voteIlabel = labels[sortDist[i]]# dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。# 计算类别次数classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1# 排序sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)# 返回次数最多的类别,即所要分类的类别return sortedClassCount[0][0]fileName = 'datingTestSet.txt'
datingDataMat, datingLabels = fileRead(fileName)
showData(datingDataMat, datingLabels)
percent = 0.10
normalDataMat, ranges, minvals = autoNorm(dataSet=datingDataMat)
m = normalDataMat.shape[0]
numTestVecs = int(m*percent)
errorCount = 0.0
for i in range(numTestVecs):classifyResult = classify(normalDataMat[i,:],normalDataMat[numTestVecs:m,:],datingLabels[numTestVecs:m],4)print("分类结果：%d,真实类别：%d" % (classifyResult,datingLabels[i]))if(classifyResult!=datingLabels[i]):errorCount += 1.0
print("错误率：%f%%" %(errorCount/float(numTestVecs)*100))

运行截图
在这里插入图片描述

这篇关于K近邻算法经典案例实现之海伦约会的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/436897。

相关文章

不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
Hadoop企业开发案例调优场景

Hadoop企业开发案例调优场景

需求 （1）需求：从1G数据中，统计每个单词出现次数。服务器3台，每台配置4G内存，4核CPU，4线程。 （2）需求分析： 1G / 128m = 8个MapTask；1个ReduceTask；1个mrAppMaster 平均每个节点运行10个 / 3台 ≈ 3个任务（4    3    3） HDFS参数调优 （1）修改：hadoop-env.sh export HDFS_NAMENOD
阅读更多...
hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

利用康拓展开将一个排列映射成一个自然数，然后就变成了普通的广搜题。 #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#inclu
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
性能分析之MySQL索引实战案例

性能分析之MySQL索引实战案例

文章目录 一、前言二、准备三、MySQL索引优化四、MySQL 索引知识回顾五、总结 一、前言 在上一讲性能工具之 JProfiler 简单登录案例分析实战中已经发现SQL没有建立索引问题，本文将一起从代码层去分析为什么没有建立索引？ 开源ERP项目地址：https://gitee.com/jishenghua/JSH_ERP 二、准备 打开IDEA找到登录请求资源路径位置
阅读更多...
深入探索协同过滤：从原理到推荐模块案例

深入探索协同过滤：从原理到推荐模块案例

文章目录 前言一、协同过滤1. 基于用户的协同过滤（UserCF）2. 基于物品的协同过滤（ItemCF）3. 相似度计算方法 二、相似度计算方法1. 欧氏距离2. 皮尔逊相关系数3. 杰卡德相似系数4. 余弦相似度 三、推荐模块案例1.基于文章的协同过滤推荐功能2.基于用户的协同过滤推荐功能 前言     在信息过载的时代，推荐系统成为连接用户与内容的桥梁。本文聚焦于
阅读更多...
csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

这是一道扩展欧几里得算法的简单应用题，这题是在湖南多校训练赛中队友ac的一道题，在比赛之后请教了队友，然后自己把它a掉 这也是自己独自做扩展欧几里得算法的题目 题意：把题意转变下就变成了：求d1*x - d2*y = f2 - f1的解,很明显用exgcd来解 下面介绍一下exgcd的一些知识点：求ax + by = c的解 一、首先求ax + by = gcd(a,b)的解 这个
阅读更多...
综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

LntonAIServer视频质量诊断功能中的抖动检测是一个专门针对视频稳定性进行分析的功能。抖动通常是指视频帧之间的不必要运动，这种运动可能是由于摄像机的移动、传输中的错误或编解码问题导致的。抖动检测对于确保视频内容的平滑性和观看体验至关重要。 优势 1. 提高图像质量 - 清晰度提升：减少抖动，提高图像的清晰度和细节表现力，使得监控画面更加真实可信。 - 细节增强：在低光条件下，抖
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
【C++】_list常用方法解析及模拟实现

【C++】_list常用方法解析及模拟实现

相信自己的力量，只要对自己始终保持信心，尽自己最大努力去完成任何事，就算事情最终结果是失败了，努力了也不留遗憾。💓💓💓 目录   ✨说在前面 🍋知识点一：什么是list？ •🌰1.list的定义 •🌰2.list的基本特性 •🌰3.常用接口介绍 🍋知识点二：list常用接口 •🌰1.默认成员函数 🔥构造函数（⭐） 🔥析构函数 •🌰2.list对象
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2