本文主要是介绍【知识】简单理解为何GCN层数越多越能覆盖多跳邻居聚合信息范围更广,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn]
背景说明
大多数博客在介绍GCN层数时候,都会提到如下几点(经总结):
- 在第一层,节点聚合来自其直接邻居的信息。
- 在第二层,由于每个节点现在包含了其直接邻居的信息,它们在聚合直接邻居的特征时,也间接地聚合了二跳邻居的信息。
- 这个过程可以继续进行,每增加一层,信息聚合的范围就扩大一跳

但我们看代码时候其实会发现,GCNCov内的操作其实是一样的,那它是如何通过叠加多层,就可以聚合多跳邻居的呢?

如何理解
其实我们需要明白一点就行:它是“间接”聚合。
比如:
第一层GCNCov时候,每个节点都能得到其一跳邻居的信息,并根据所有邻居的信息更新自己的信息。这个没有问题,很好理解。
然后我们需要意识到,更新后的节点,实际上已经包含了其所有邻居的信息了。相应的,当前节点的邻居,也包含了它自己的邻居信息。
那么,在做第二层GCNCov时候,由于邻居节点包含了邻居节点的邻居,所以当前节点就间接地包含了二跳的邻居信息。
因此,我们实际上也可以发现,在做这两次GCNCov时候,其一跳邻居的信息被利用了多次,会造成冗余。此外,随着层数的增加,由于“间接”也在增加,似乎越远的节点信息对当前节点的贡献也会变弱。
此外,过多的层可能导致过度平滑(over-smoothing)问题,即不同节点的特征变得越来越相似,损失了区分度。
因此,层数越多效果越差,似乎也可以解释了:

最后,再画个图理解一下:
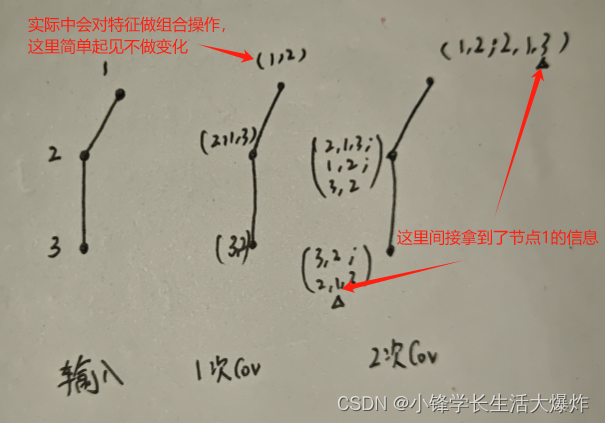
这篇关于【知识】简单理解为何GCN层数越多越能覆盖多跳邻居聚合信息范围更广的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







