Allegro DFM Ravel Rule 丝印线段到PAD 间距检查

2023-11-29 16:50

文章标签 检查线段 pad allegro rule 间距丝印 dfm ravel

本文主要是介绍Allegro DFM Ravel Rule 丝印线段到PAD 间距检查，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Allegro DFM Ravel Rule 丝印线段到PAD 间距检查

下面介绍丝印线段到pad的间距检查
在这里插入图片描述

检查top层丝印线段到过孔间距，默认值是1mil，可以根据需要更改这个数值
检查bottom层丝印线段到过孔间距
检查top层丝印线段到通孔pin间距
检查bottom层丝印线段到通孔pin间距
检查top层丝印线段到表贴pin间距
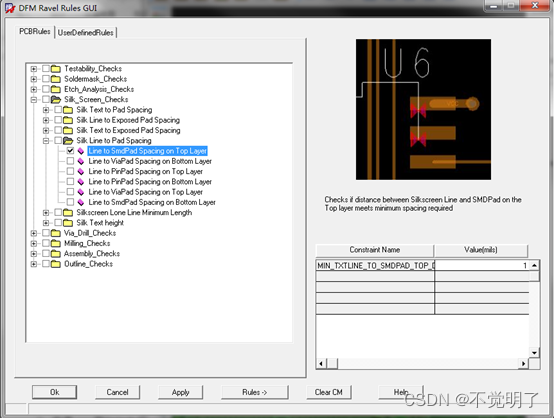
检查top层丝印线段到表贴pin间距

这篇关于Allegro DFM Ravel Rule 丝印线段到PAD 间距检查的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/433584。 23002807@qq.com

shell脚本快速检查192.168.1网段ip是否在用的方法

《shell脚本快速检查192.168.1网段ip是否在用的方法》该Shell脚本通过并发ping命令检查192.168.1网段中哪些IP地址正在使用,脚本定义了网络段、超时时间和并行扫描数量,并使用... 目录脚本：检查 192.168.1 网段 IP 是否在用脚本说明使用方法示例输出优化建议总结检查 1

使用Python检查CPU型号并弹出警告信息

《使用Python检查CPU型号并弹出警告信息》本教程将指导你如何编写一个Python程序,该程序能够在启动时检查计算机的CPU型号,如果检测到CPU型号包含“I3”,则会弹出一个警告窗口,感兴趣的小... 目录教程目标方法一所需库步骤一：安装所需库步骤二：编写python程序步骤三：运行程序注意事项方法二

poj3468(线段树成段更新模板题)

题意：包括两个操作：1、将[a.b]上的数字加上v；2、查询区间[a,b]上的和下面的介绍是下解题思路：首先介绍 lazy－tag思想：用一个变量记录每一个线段树节点的变化值，当这部分线段的一致性被破坏我们就将这个变化值传递给子区间，大大增加了线段树的效率。比如现在需要对[a,b]区间值进行加c操作，那么就从根节点[1,n]开始调用update函数进行操作，如果刚好执行到一个子节点，

hdu1394(线段树点更新的应用)

题意：求一个序列经过一定的操作得到的序列的最小逆序数这题会用到逆序数的一个性质，在0到n-1这些数字组成的乱序排列，将第一个数字A移到最后一位，得到的逆序数为res-a+(n-a-1) 知道上面的知识点后，可以用暴力来解代码如下： #include<iostream>#include<algorithm>#include<cstring>#include<stack>#in

hdu1689(线段树成段更新)

两种操作：1、set区间[a,b]上数字为v；2、查询[ 1 , n ]上的sum 代码如下： #include<iostream>#include<algorithm>#include<cstring>#include<stack>#include<queue>#include<set>#include<map>#include<stdio.h>#include<stdl

hdu 1754 I Hate It（线段树，单点更新，区间最值）

题意是求一个线段中的最大数。线段树的模板题，试用了一下交大的模板。效率有点略低。代码： #include <stdio.h>#include <string.h>#define TREE_SIZE (1 << (20))//const int TREE_SIZE = 200000 + 10;int max(int a, int b){return a > b ? a :

hdu 1166 敌兵布阵（树状数组 or 线段树）

题意是求一个线段的和，在线段上可以进行加减的修改。树状数组的模板题。代码： #include <stdio.h>#include <string.h>const int maxn = 50000 + 1;int c[maxn];int n;int lowbit(int x){return x & -x;}void add(int x, int num){while

poj 1127 线段相交的判定

题意：有n根木棍，每根的端点坐标分别是 px, py, qx, qy。判断每对木棍是否相连，当他们之间有公共点时，就认为他们相连。并且通过相连的木棍相连的木棍也是相连的。解析：线段相交的判定。首先，模板中的线段相交是不判端点的，所以要加一个端点在直线上的判定；然后，端点在直线上的判定这个函数是不判定两个端点是同一个端点的情况的，所以要加是否端点相等的判断。最后

HDU4737线段树

题目大意：给定一系列数，F(i,j)表示对从ai到aj连续求或运算，(i<=j)求F(i,j)<=m的总数。 const int Max_N = 100008 ;int sum[Max_N<<2] , x[Max_N] ;int n , m ;void push_up(int t){sum[t] = sum[t<<1] | sum[t<<1|1] ;}void upd

zoj 1721 判断2条线段（完全）相交

给出起点，终点，与一些障碍线段。求起点到终点的最短路。枚举2点的距离，然后最短路。 2点可达条件：没有线段与这2点所构成的线段（完全）相交。 const double eps = 1e-8 ;double add(double x , double y){if(fabs(x+y) < eps*(fabs(x) + fabs(y))) return 0 ;return x + y ;

Allegro DFM Ravel Rule 丝印线段到PAD 间距检查

相关文章