本文主要是介绍PWM占空比原理是什么,几个实例带你进一步了解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
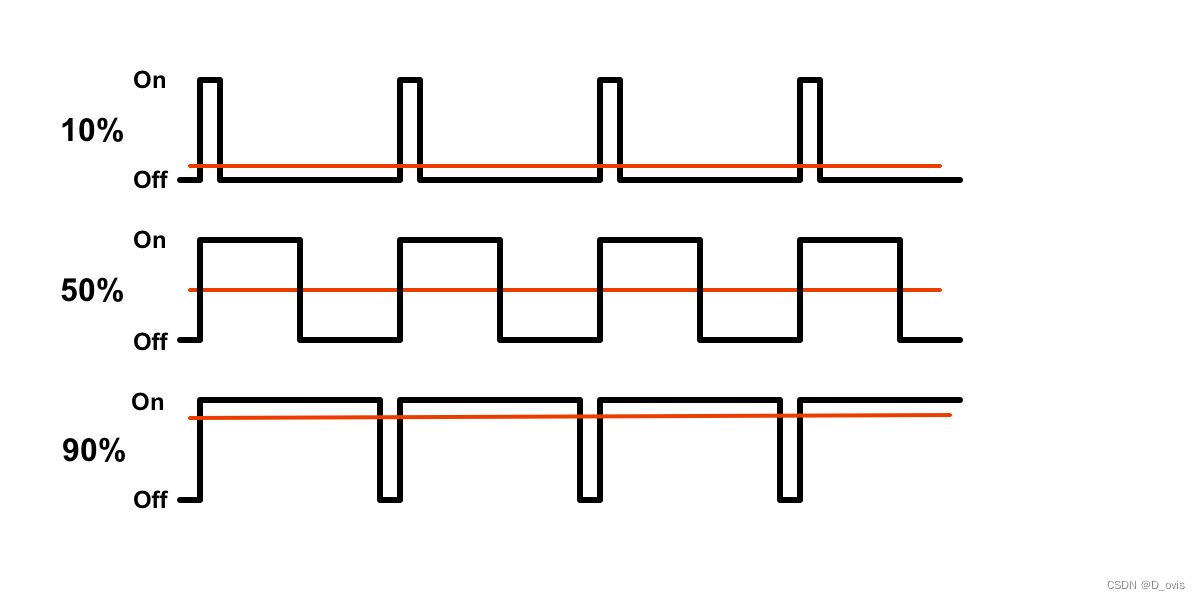
在电力电子技术中,对于很多变量的控制,我们可以采取模拟的方式,也可以采用数字的方式进行处理。例如,在简单的模拟收音机中,音量旋钮被连接到一个可变电阻。拧动旋钮时,电阻值变大或变小;流经这个电阻的电流也随之增加或减少,从而改变了驱动扬声器的电流值,是音量响应变大或变小。与收音机一样,模拟电路的输出与输入成线性比例。尽管模拟控制看起来可能简单而直观,但它并不总是经济的或可行的。其功耗、一些物理的扰动都可能对我们的设备造成干扰。而通过数字方式控制模拟电路,可以大幅度降低系统的成本和功耗。

同样的,在嵌入式领域中,PWM也多有用途。现在的单片机中,大多有PWM模块,也称之为PWM定时器。实际应用过程中,会根据某物理量对于不同参量的敏感度不同而使用不同的处理方式。举两个简单的小例子。如:处理led时,led灯的亮度是电压敏感的,使用PWM时,就会通过调节其占空比(一个脉冲周期内高电平在整个周期占的比例),从而控制电压值,来干预led灯的亮度。在处理蜂鸣器时,由于其对频率是敏感的,频率越高音调越高,因此,使用PWM进行调节时,我们通过修改PWM的频率,来调节蜂鸣器的音调。
具体的原理可以参照《嵌入式Linux应用开发完全手册》。以下奉送个小实例供大家参考:
实例:通过调节占空比(用按键实现),来改变电压值的大小,从而控制led灯的亮度。
///main.c//
#include "common.h"
#include "led.h"
#include "key.h"
/* 增大占空比 */
void add_cb(void *arg)
{
*(int *)arg += 100;
if (*(int *)arg > 1000){
*(int *)arg = 1000;
}
}
/* 减小占空比 */
void dec_cb(void *arg)
{
*(int *)arg -= 100;
if (*(int *)arg < 0)
*(int *)arg = 0;
}
int main(void)
{
int i = 0;
int cmp = 0;
key_t k2, k3;
led_t led5;
/* 初始化按键、LED */
key_init(&k2, 0x11000c20, 0x11000c24, 1); /* gpx1_1 */
key_init(&k3, 0x11000c20, 0x11000c24, 2); /* gpx1_2 */
led_init(&led5, 0x114001E0, 0x114001E4, 5); /* gpf3_5 */
while(1){
key_query(&k2, dec_cb, &cmp); // k2减小cmp比较值,减小占空比
key_query(&k3, add_cb, &cmp); // k3增大cmp值,增大占空比
/* 输出一次PWM信号 */
for (i = 0; i < 1000; i ++){
if(i < cmp)
led_on(&led5);
else
led_off(&led5);
}
}
return 0;
}
///led.c///
#include "led.h"
#define __REG(x) (*(volatile unsigned int *)(x))
/* LED的方法 */
void led_init(struct led *led, int con, int dat, int pin) //初始化LED对象
{
led->con = con;
led->dat = dat;
led->pin = pin;
/* 把相应pin引脚设置为输出模式 */
__REG(con) = __REG(con) & ~(0xF<<(pin*4)) | (0x1<<(pin*4));
}
//打开LED
void led_on(struct led *led)
{
__REG(led->dat) |= (1
}
void led_off(struct led *led) //关闭LED
{
__REG(led->dat) &= ~(1
}
void led_toggle(struct led *led) //LED状态取反
{
__REG(led->dat) ^= (1
}
//key.c
#include "key.h"
#define __REG(x) (*(volatile unsigned int *)(x))
void key_init(key_t *key, unsigned int con, unsigned int dat, unsigned int pin)
{
key->con = con;
key->dat = dat;
key->pin = pin;
/* 把CON寄存器的相应位清零,
* 表示设置相应引脚为输入模式 */
__REG(key->con) &= ~(0xF<<(pin * 4));
}
/* 判断按键是否按下 */
int key_query(key_t *key, void (*callback)(void *), void *arg)
{
if ((__REG(key->dat) & (1<<(key->pin))) == 0){
mdelay(50); /* 消除按键抖动 */
if ((__REG(key->dat) & (1<<(key->pin))) == 0){
callback(arg); /* 执行回调函数 */
while ((__REG(key->dat) & (1<<(key->pin))) == 0);
return 1;
}
}
return 0;
}
嵌入式物联网需要学的东西真的非常多,千万不要学错了路线和内容,导致工资要不上去!
无偿分享大家一个资料包,差不多150多G。里面学习内容、面经、项目都比较新也比较全!某鱼上买估计至少要好几十。(点击找小助理领取)
这篇关于PWM占空比原理是什么,几个实例带你进一步了解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



