本文主要是介绍算法和数据结构篇---带环链表的问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题简述
一个单向链表,如果后面的节点的下一节点是之前的某个节点,那这就叫带环链表。既然有带环链表,那就涉及到一系列问题了,如何判断一个链表是否带环,如果带环,那环的长度为多少?环的入口节点是哪一个?从头节点到入口节点的长度是多少?下面就来分析一下这个问题
分析
首先写一个环出来
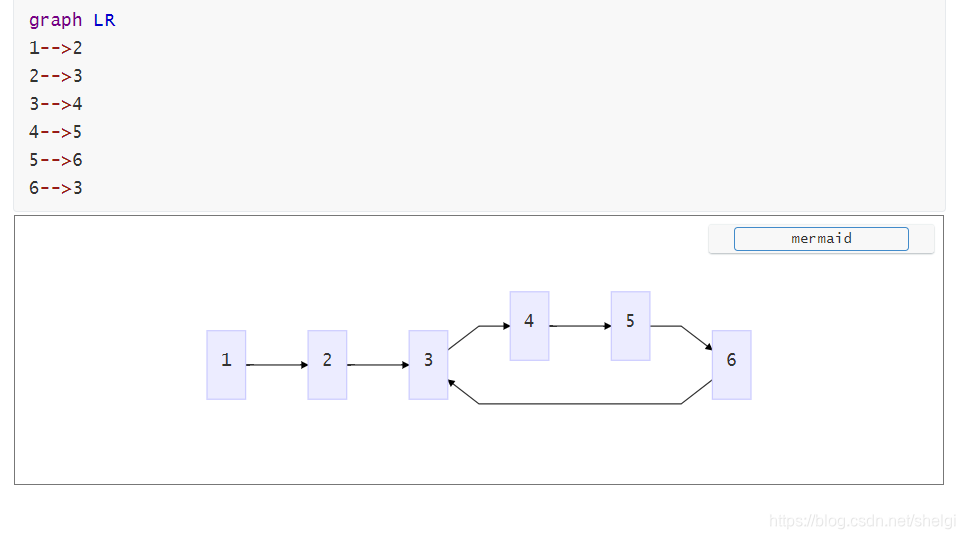
如何判断有没有环?设置两个节点p1,p2;他们的初值都是头节点1,然后开始让他们分别遍历链表,p1每次往后移一个节点,p2每次往后移两个节点,如果p1和p2最后能遇到,则证明有环存在,反之就没有环。
那知道有环存在怎么得到环的长度
首先得到p1,p2的第一次相遇点,然后继续遍历,还是根据上面的规则,等他们再次相遇时,刚好p2比p1多走了一个环的长度,那么环的长度就是
L=2次数-1次数=次数,也就是把求环长度的问题转换成了求第一次到第二次相遇需要经过几次。
入口节点我们从图上可以看得出是3,那怎么用算法实现
假设头节点到入环节点的距离为x,入环节点到首次相遇点的距离为s1,首次相遇点到入环节点的距离为s2
开始一个简单的计算,相遇时
p1的路程=x+s1
p2的路程=x+s1+s2+s1
p2的路程是p1的两倍,所以x+2s1+s2=2x+2s1
得到x=s2,也就是说从头节点到入环节点的距离等于首次相遇点到入环节点的距离,那我们可以在头节点放一个p1,首次相遇点放一个p2,他们每次都往后移一位,那么相遇时的节点就是入环节点,移动的次数就是头节点到入环节点的长度。
上代码
package 环形链表判断;public class 判断链表是否有环 {//链表节点private static class Node{int data;Node next;Node(int data){this.data = data;}}//判断是否有环//思路:相当于追击,p1每次往后移一个节点,p2每次往后移两个节点。如果有环则p1,p2必会相遇,否则就表示链表中不存在环。public static boolean iscycle(Node head){Node p1=head;Node p2=head;while(p2!=null && p2.next!=null){p1=p1.next;p2=p2.next.next;if(p1==p2)return true;}return false;}//求环的长度,len=2*移动次数-1*移动次数public static int cycle_length(Node head){Node p1=head;Node p2=head;p1=p1.next;p2=p2.next.next;int len=1;while(p1!=p2){p1=p1.next;p2=p2.next.next;len++;}return len;}public static Node meet(Node head){Node p1=head;Node p2=head;Node p=head;p1=p1.next;p2=p2.next.next;while(p1!=p2){p1=p1.next;p2=p2.next.next;}p=p1;return p;}//求入环节点public static int enter(Node head){Node p1=head;Node p2=meet(head);Node p=head;p1=p1.next;p2=p2.next;while(p1!=p2){p1=p1.next;p2=p2.next;}p=p1;return p.data;}//求链表的头节点到入环节点的距离public static int len(Node head){Node p1=head;Node p2=meet(head);Node p=head;p1=p1.next;p2=p2.next;int len=0;while(p1!=p2){p1=p1.next;p2=p2.next;}p=p1;p2=meet(head);while(p2!=p){p2=p2.next;len++;}return len;}public static void main(String[] args) throws Exception {Node node1 = new Node(5);Node node2 = new Node(3);Node node3 = new Node(7);Node node4 = new Node(2);Node node5 = new Node(6);Node node6 = new Node(8);node1.next = node2;node2.next = node3;node3.next = node4;node4.next = node5;node5.next = node6;node6.next = node3;/*创建的链表结构为,括号内是节点的值6(8)<--5(6)| |1(5)--->2(3)--->3(7)--->4(2)*/System.out.println("链表中存在环的结果为:" + iscycle(node1));if (iscycle(node1)){System.out.println("链表中环的长度为:" + cycle_length(node1));System.out.println("链表中相遇节点的值为:"+meet(node1).data);System.out.println("链表中环入口节点的值为:" + enter(node1));System.out.println("链表的头节点到交点的距离为:"+len(node1));}elseSystem.out.println("该链表不存在环");}
}
结果
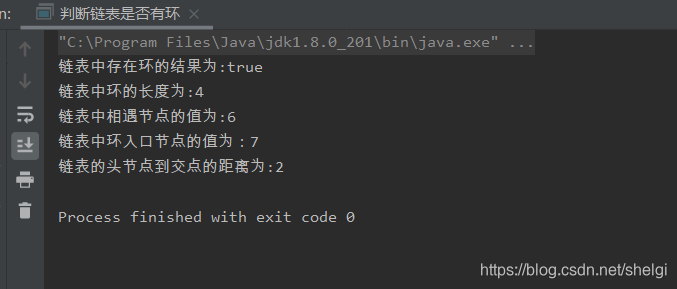
这篇关于算法和数据结构篇---带环链表的问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






